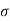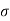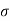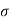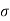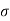undefined | unit 1 introduction to various design philosophies

Back to Study material

DCS

Unit-1

Introduction to Various Design Philosophies

Q1) Explain introduction to various design philosophies of R.C structure?

A1) Concrete is strong in compression but week in tension

Steel is reinforced suitable at the place where concrete is weak in tension such combination of steel and concrete

The purpose of R.C structure is increase strength of concrete section and to reduce the size of structural member

Various design philosophies of R.C structure are

Working stress method (WSM)

Ultimate load method (ULM)

Limit state method (LSM)

Reinforced concrete is used to construct various structures

Buildings

Bridges

Flyovers

Water tanks

Retaining wall

Bunkers and silos

Chimney

Towers

Concrete roads

Building construction in Sydney Australia - Upto The Point

Water Tanks Construction - Water Tanks Construction Services Distributor / Channel Partner from Mysore Fig no 1Building

Gov't Defends Decision to Hive off Part of Uhuru Park for JKIA-Westlands Expressway | Mwakilishi.com

Fig no 2 Fig no 3

Flyover Water tank

Q2) Explain various type of RCC structure also limitations of WSM over LSM

A2) Following are the various methods for RCC structure

1. Working stress methodology (WSM).

2. Ultimate load methodology (ULM).

3 Limit state methodology (LSM).

Limitations of WSM strategies over LSM

Since WSM supported elastic theory, the reserve strength materials on the far side yield purpose isn't taken under consideration

In operating stress methodology, serviceableness criteria isn't taken into thought, moment of resistance for same cross section is additional in LSM than WSM.

Q3) Explain advantages and disadvantages of RCC

A3) Advantages of reinforced concrete

Strength

Ductility

Durability

Mould ability

Porosity

Fire place resistance

Economy

1. Strength

It has excellent Tensile likewise as compressive strength a pair of malleability

2. Ductility

Ductility of structures is increase thanks to steel reinforcement

3. Durability

R.C. structures are more durable

4. Mould ability

The flexibility of reinforcement and therefore the liquidness of concrete makes the R.C. member to be mould in any form thus it's appropriate for architectural demand.

5. Porosity

RC members are impermeable to wet

6. Fire place resistance

R.C. structures are additional fireplace resistance than alternative materials such as steel and wood

7. Economy

R.C.C is cheaper than steel and pre stressed concrete

Disadvantages of R.C.C

RCC has followed disadvantages

1. Weight of R.C. structures are measure over different materials

2. Significant formwork is needed for R.C. members

3. RC structures take a lot of times to realize its full strength

Q4) Explain the working stress methods, ultimate load methods, limit state methods

A4) Working Stress Method (WSM)

WSM one of the oldest method of design of structures WSM

It is based on the elastic theory.

In WSM, a structural clement is so designed that the permissible stresses are not exceeded anywhere in the structures when it is subjected to worst combination of working loads

In WSM, the reserve strength to materials beyond yield point is not taken into account.

The permissible stress in concrete is obtained by the ratio of ultimate strength of concrete to factor of safety

The permissible stress in steel is obtained by the ratio of yield strength or 02 proof stress of steel to factor of safety

As per 15456, factor of safety of 3 for concrete and 1.78 for yield strength of steel.

Ultimate Load Method

In this method, ultimate load is used as a design load

Working loads are increased by while factor 1.5 times ultimate loads. These factors we called as load factors

This load factors give the exact margin of safety in term of load

Nonlinear stress strain behavior of concrete is taken into account

Load factor= Collapse load / working load

This theory is based on the belief that final strain in concrete in and therefore the compressive stress at the sting of the section correspond to the present strain.

The ULM is most economical than WSM the section designed by final load strategies square measure and needed less reinforcement.

The most drawback of the this method is as follow

Very skinny section obtained by this technique ends up in excessive deformations and cracking, that the structures become unserviceable.

No issue of safety is employed for material stresses.

As the serviceability demand isn't glad by this technique, it absolutely was not adopted by structural designers.

Ultimate load technique is replaced by Limit state technique that takes care of state of collapse and serviceableness.

Limit State methods

Limit state technique is associate degree improved style philosophy to beat the drawbacks of WSM and ULM

It is supported semi-empirical approach. Limit states square measure the assorted necessities that structure is predicted to complete so the performance of the structure satisfies the supposed purpose that it's engineered.

it's the great technique which is able to beware of each strength and serviceableness necessities

IS 456 2000 is employed to style the plain and strengthened concrete by this technique. It thought-about limit state for collapse and serviceableness

Limit state of collapse square measure axial ( tension and compression ) flexure, shear and torsion

Limit state of serviceableness square measure deflection ,durability, fireplace resistance

Q5) What are the assumption created in working stress methods

A5) Assumptions created in working stress method

Sections that a plane before bending stay plane even when bending

The stress-strain relationship for concrete and steel under working load is liner

The standard modular ratio m has the worth of 280/3rho

All tensile stresses area unit preoccupied by steel reinforcement only and also the concrete areas in tension one is chosen

There should be an ideal bond between steel and tensile and compressive forces

The modulus of elasticity steel and concrete are constant

Q6) Explain the comparison between balanced, under reinforced. Over reinforced section

A6) Comparison between various sections

S R NO	Description	Balanced Section	Under reinforcement section	Over reinforcement section
1	Steel	Steel provided as per requirements	Steel provide less than requirements	Steel provided more than requirements
2	Neutral axis	X =XC	X<XC	X>XC
3	Actual stress of concrete	(c b c) s= 𝜎c b c	(c b c) s< 𝜎c b c	(c b c) s= 𝜎c b c
4	Actual stress in steel	(s t )s= 𝜎s t	(s t)s= 𝜎s t	(s t)s< 𝜎s t
5	Moment of resistance	MR =TZ =CZ	MR = T*Z	MR =C*Z
6	Economic	economical	More economical	costlier
7	Safety	More safe	Fails in tension	Fails in compression

Q7) A reinforced concrete beam section of size 300 mm x 700 mm effective depth is reinforced with 3 bars of 20 mm diameter in tension. The concrete mix and HYSD steel reinforcement used are of grade M20 and Fe415 respectively.

A7) Find

1) Depth of neutral axis.

2) Type of reinforced section.

3) Moment of resistance.

4) Maximum stress induced in material WSM is recommended.

Answer:

Given,

b = 300 mm

d = 700 mm

To find: x, MR and σc b c

Sol2

For M20, σc b c = 7 N/mm2 and m = 280 / 3 * 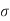c b c = 230/ 3* 7 = 13.33

For Fe415, σs t = 230 N/mm2

Area of steel = n * 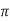/2 * d 2 = 942.5 mm 2

Step 1: Depth of critical neutral axis:

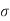c b c / (s t /m) = X c / (d –X c)

0.406 = X c / (700 – X c)

700 = x c + 2.464 X c

X C = 202

Step 2: Actual depth of neutral axis (x):

= m. A s t( d – x)

= 13.33x942.5 (700– x)

150 x2 = 8.794 x 106 – 12563.53x

150 x2 + 12563.53x - 8.794 x 106 = 0

Solving quadratic equation, we get

x = 203.85 mm

Step 3: Type of beam section:

Since, x > X c, then section is over reinforced section and will be fails

in compression.

Step 4: Moment of resistance:

MR = C* Z

MR = 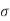c b c/ 2 .b .x. (d – x/3)

= 300 X 203.85 (700–203.85 /3)

= 135.29 x 106 N.mm = 135.29 K N. m

Step 5: maximum stress induced in material:

Since the section fails in compression,

c b c max = 7 N/ mm 2

Corresponding maximum stress in steel:

= c b c /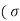s t/m) = x – (d-x)

= 93.33/ 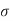s t = 0.41086

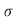s t max= 227.1 N/mm2

Q8) What are assumption in limit state design

A8) ASSUMPTION IN LIMIT STATE DESIGN

At Limiting state, the utmost strain in concrete, that happens at outer compression fiber is 0.0035

The stress-strain curve for concrete has parabolic get on to 0.002 strain and also the constant up to limit state of 0.0035.However, IS Code doesn't stop alternative shapes like parallelogram and trapezoidal

The lastingness of concrete is ignored

The stress in reinforcement springs from the representative stress-strain curve for the kind of steel used .For style purpose a partial ratio of 1.15 is used thus maximum stress in steel is proscribed to f y/1.15= 0.87 * f y

.The most strain in steel at failure shall not be less than

F y/1.15Es + 0.002 f y

Q9) What are the design steps for finding ultimate moment of resistance

A9) DESIGN STEPS

Calculation of ultimate moment of resistance

Given

Grade of concrete

Grade of steel

Size of beam

Reinforcement provided

If X u = X u max …………….balanced

If X u< X u max …………….under reinforced

If X u> X u max …………….over reinforced

Equating the compression force and tension force

0.36 * f c k * b * X u * + A s c * f s c = 0.87 * f y * A s t

From this find X u

Moment of resistance

M u = 0.36 * f c k * b * X u * (d- 0.42 * X u) + A s c * f s c * (d- d’)

This equation is valid for balanced and under reinforced section

If the section is over reinforced section then take X u = X u max in above equation and use the same equation for finding M u .Do not increase the depth of the beam for over reinforced section.

Design the beam find out reinforcement

Given

Grade of concrete and steel

Size of beam

Ultimate moment

M u is given

For balanced section X u = X u max

M u limiting = 0.36 * f c k * b * X u max * (d- 0.42 * X u max)

So M u 2 = M u – M u limiting

A s t limit = M u limit / 0.87 * f y * (d – 0.42 * X u max)

A sc = M u2/ f s c (d- d’)

As t 2 = A s c * f s c/ 0.87 f y

As t =A s t limit + A s t 2

Where

d = effective depth of beam

d’= distance between extreme compression fiber to the center of comp reinforced

b = width of beam

X u = depth of actual neutral axis

X u max = depth of critical neutral axis

A s t = total area of tensile reinforced in mm2

F c k = characteristic compressive strength of concrete

F y = characteristic strength of steel

M u limit = limiting M R of a section without compression reinforced in K N m Top of Form

M u = ultimate M R

A s c= area of compression reinforcement

Q10) Explain L beam brief

A10)L BEAM

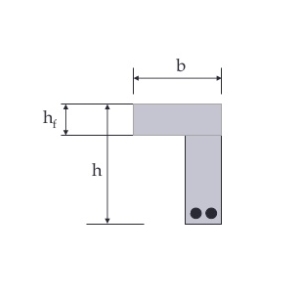
T-Beams...PRC_I

Fig no 4 L BEAM

In bending the beam take the tension force and slab take compression force since the L beam receive their load from one side only they are subjected to consideration amount of torsion moments so L beam are subjected to bending moments shear force and torsion moments

Moment carried by flange of L beams

The moment M1 causes torsion in the beam and is known as the torsion moments which is restricted by the rectangular portion only and the flanged does not contribute to torsion moment of resistance

Moment carried by flanged of L beam and the slab

The central load W cause bending moments in the beam which is joined restricted by the rectangular portion of the beam as well as the flanged

Changes in floor level may be accommodated by either an L beam or building up one side of an inverted T beam

Code recommends that effective width of the flanged of beam may be taken as follows

For L beam ,lesser of

b f =I o /12 + b w + 3 D f

b f = X 1 + b w

2. for isolated L beams ,lesser of

b f = 0.5 I o /( I o +b )4 + b w

b f = b

Where

b f = effective width of flanged

b w =breadth of rib

b = actual width of flanged

I o = distance between points of zero moments in beam

The design principles to be followed while designing L beam

Given

type of mix

thickness of slab

bending and shear force

Step 1: determine width of flanged

Steps 2: fixed up a suitable depth

Steps 3: calculate MR of the section assuming the failure of concrete to occur .if the moment of resistance is greater than bending moments assumed depth is ok otherwise either increases the depth of the section or provide additional reinforcement in compression side in addition to the tension side

Steps 4: calculate the amount of tension steel for actual bending moments treating it as a balanced section

Steps 5: check for the shear and provide shear reinforced

Steps 6: check of deflection

Steps 7: check for end anchoring and development length

Sign Up