Unit-2
Geometric Design
Q1) Calculate the stopping sight distance for design speed of 50 kmph for (a) two-way traffic on a two lane road, (b) Two way traffic on a single plane road.
Assume coefficient of friction as 0.37 and reaction time of driver as 2.5 second.
A1)
Stopping distance = Lag distance + Braking Distance
= vt +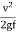 
V = 50 kmph or v = 60/3.6 = 13.9 m/sec
T = 2.5 second, g = 9.81 m/sec2, f = 0.37
Stopping Distance = 13.9 X 2.5 +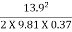 
= 34.8 + 26.6 = 61.4m
(a) Stopping sight distance when there are two lanes = stopping distance = 61.4m
(b) Stopping sight distance for two-way traffic with single lane = 2(stopping distance) = 2 X 61.4 = 122.8 m
Q2) Calculate the minimum sight distance required to avoid a head-on-collision of two cars approaching from the opposite directions at 90 kmph and 60 kmph. Assume a reaction time of 2.5 seconds, coefficient of friction of 0.7 and a brake efficiency of 50%, in either case.
A2) Stooping distance for one of the cars
Stopping distance = vt + 
V1 = 90 kmph = 90/3.6 = 25 m/sec
V2 = 60 kmph = 60/3.6 = 16.67 m/sec
As the brake efficiency is 50%, the wheels will skid 50% of the braking distance and rotate through the remaining distance. Therefore, the value of coefficient of friction developed f may be taken as 50% of the coefficient of friction, i.e.,
f = 0.5 X 0.7 = 0.35
The stopping distance for car SD1 = 25 X 2.5 +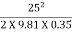 
= 153.6 m
The stopping distance for car SD2 = 16.67 X 2.5 + 
= 82.2 m
Sight distance to avoid head-on-collision of the two approaching cars,
= SD1 + SD2
= 153.6 + 82.2
= 235.8 m
Q3) Calculate the safe overtaking sight distance for a design speed of 96 kmph. Assume all other data suitably.
A3)
O.S.D = (d1 + d2) ----for one-way traffic
O.S.D = (d1 + d2 + d3) ----for two-way traffic
V = 96 kmph
Assume, Vb = V - 16 = 80kmph and
A 2.5kmph/sec, t = 2 second
d1 = 0.28 Vb t = 0.28 X 80 X 2 = 44.8 m
d2 = 0.28 Vb t + 2s
Where, s = 0.2 Vb + 6 = 0.2 X 80 + 6 =22 m
T = 
= 
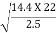= 11.3 second
d2 = 0.28 X 80 X 11.3 + 2 X 22 =297 m
d3 = 0.28 VT = 0.28 X 96 X 11.3 = 303.7 m
O.S.D on one-way traffic road = (d1 + d2) = 44.8 + 297 = 341.8 Say = 342 m
O.S.D on two-way traffic road = (d1 + d2 + d3) = 44.8 + 297 + 303.7 = 645.5 m
Say = 646
Q4) The radius of a horizontal circular curve is 100 m. The design speed is 50 kmph and the design coefficient of lateral friction is 0.15.
(a) Calculate the super elevation required if full lateral friction is assumed to develop.
(b) Calculate the coefficient of friction needed if no super elevation is provided.
(c) Calculate the equilibrium super elevation if the pressure on inner and outer wheels should be equal.
A4)
(a) Super elevation is given by the relation
e + f =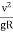 
= 
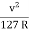
Here,
f = 0.15 and V = 50kmph or v = 50/3.6 m/sec
R = 100 m
e + 0.15 =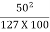 
= 0.917
e = 0.917 – 0.15 = 0.047
i.e., super elevation rate is 1 in 21.2.
(b) If no super elevation is provided, e = 0 and friction factor developed,
f =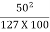 
= 0.917
(c) For the pressure on inner and outer wheels to be equal or for equilibrium super elevation counteracting centrifugal force fully, f = 0 and
e =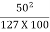 
= 0.917
i.e., equilibrium super elevation rate is 1 in 5.1.
However, this rate of super elevation being very high cannot be provided.
Q5) Explain camber. What are the objects of camber? Discuss the factors on which the amount of camber to be provided depends.
A5)
Camber or Cant is the cross slope provided to raise middle of the road surface in the transverse direction to drain of rain water from road surface.
The objectives of providing the camber are
Depending on the type of road surface and amount of rainfall, following camber is suggested by IRC:
Surface Type | Heavy Rain | Light Rain |
Concrete/Bituminous | 2% | 1.7% |
Gravel/WBM | 3% | 2.5% |
Earthen | 4% | 3% |
Excessive camber or cross slope should be avoided because
Different types of Camber:
Q6) Explain the sight distance and factors causing restrictions to sight distance.
A6)
The safe and efficient operation of vehicles on the road depends very much on the visibility of the road ahead of the driver. Thus the geometric design of the road should be done such that any obstruction on the road length could be visible to the driver from some distance ahead. This distance is said to be the sight distance.
For straight road on level ground, there is no problem of side distance. But Straight road on a level ground is a rare case. Horizontal curves, vertical curves (Summit), intersections are potential places where there could be restriction in terms of Sight distance
Actual distance along the road surface over which a driver from specified height above the carriageway has visibility of stationary or moving object.
The sight distance used for design is
Stopping Sight Distance (SSD) or absolute minimum sight distance
Intermediate Sight Distance (ISD) = 2*SSD
Overtaking Sight Distance (OSD) for safe overtaking
Headlight Sight Distance = SSD at night
Intermediate sight distance: - Intermediate sight distance (ISD) is defined as twice SSD. Overtaking sight distance (OSD) for safe overtaking operation. Head light sight distance is the distance visible to a driver during night driving under the illumination of head lights.
Overtaking sight distance: - The overtaking sight distance is the minimum distance open to the vision of the driver of a vehicle intending to overtake the slow vehicle ahead safely against the traffic in the opposite direction.
Headlight sight distance: -Head light sight distance is the distance visible to a driver during night driving under the illumination of head lights.
Q7) Why are overtaking zones are provided?
A7)
The overtaking sight distance is the minimum distance open to the vision of the driver of a vehicle intending to overtake the slow vehicle ahead safely against the traffic in the opposite direction. The overtaking sight distance or passing sight distance is measured along the center line of the road over which a driver with his eye level 1.2 m above the road surface can see the top of an object 1.2 m above the road surface.
The factors that affect the OSD are:
1. Velocities of the overtaking vehicle, overtaken vehicle and of the vehicle coming in the opposite direction.
2. Spacing between vehicles, which in-turn depends on the speed
3. Skill and reaction time of the driver
4. Rate of acceleration of overtaking vehicle
5. Gradient of the road
Q8) Explain briefly extra widening.
A8)
Extra widening refers to the additional width of carriageway that is required on a curved section of a road over and above that required on a straight alignment.
This widening is done due to two reasons: the first and most important is the additional width required for a vehicle taking a horizontal curve and the second is due to the tendency of the drivers to ply away from the edge of the carriageway as they drive on a curve.
The first is referred as the mechanical widening and the second is called the psychological widening.
Mechanical Widening:
When a vehicle negotiates a horizontal curve, the rear wheels follow a path of shorter radius than the front wheels. This phenomenon is called off tracking, and has the effect of increasing the effective width of a road space required by the vehicle.
Therefore, to provide the same clearance between vehicles traveling in opposite direction on curved roads as is provided on straight sections, there must be extra width of carriageway available.
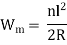
Where,
Wm = Mechanical Widening
n = Number of Lanes
R = Radius of Curve
Psychological Widening:
There is a tendency for the drivers to drive close to the edges of the pavement on curves. Some extra space is to be provided for more clearance for the crossing and overtaking operations on curves.
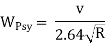
Q9) Discuss the requirements of summit curves and its shapes.
A9)
Summit curves or crest curves are convex upwards. If Deflection Angle N is Positive, the vertical curve is Summit Curve. If road surface is below the point of vertical intersection, then it is summit curve
Summit Curves are formed when two gradients meet as illustrated below:
1. Shape of Summit Curve
Circular summit curves are ideal as the sight distance available throughout the length of summit curve is constant.
For small deviation angle, simple parabola is congruent with a circular curve.
Arithmetic calculations and ordinates computation are easy for simple parabola. So, general practice is to provide simple parabola as Summit curve
2. Design Considerations
The stopping sight distance or absolute minimum sight distance should be provided on these curves and where overtaking is not prohibited, overtaking sight distance or intermediate sight distance should be provided as far as possible.
When a fast moving vehicle travels along a summit curve, there is less discomfort to the passengers. This is because the centrifugal force will be acting upwards while the vehicle negotiates a summit curve which is against the gravity and hence a part of the tyre pressure is relieved.
P: Centrifugal Force
W: Gravitational Force
3. Length of Summit Curve (IRC Approach)
The important design aspect of the summit curve is the determination of the length of the curve (L) which is parabolic. As noted earlier, the length of the curve is guided by the sight distance consideration (S). That is, a driver should be able to stop his vehicle safely if there is an obstruction on the other side of the road.
While deciding the length of summit curve, two situations can arise depending on the uphill and downhill gradients
When the length of the curve is greater than the sight distance (L>S)
When the length of the curve is greater than the sight distance ((L<S)
Case 1: L>S
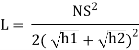
Where,
L: Length of Summit Curve
S: Sight Distance (S: SSD – when obstruction is stationary)
(S: OSD/ISD – when obstruction is moving)
N: Deviation Angle
h1: Drivers Eye Height = 1.2m
h2: Height of Obstruction = 0.15m
Case 2: L<S
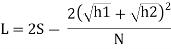
When stopping sight distance (SSD) is considered the height of driver's eye above the road surface (h1) is taken as 1.2 meters, and height of object above the pavement surface (h2) is taken as 0.15 meters.
Q10) Explain the factors based on which the length of valley curve is designed.
A10)
Valley curves or sag curves are convex downwards. If Deflection Angle N is Negative, the vertical curve is Valley Curve. If road surface is above the point of vertical intersection, then it is Valley curve.
Valley Curves are formed when two gradients meet as illustrated below:
Design Considerations
There is no restriction to sight distance at valley curves during day time. But visibility is reduced during night. In the absence or inadequacy of street light, the only source for visibility is with the help of headlights. Hence valley curves are designed taking into account of headlight distance.
In valley curves, the centrifugal force will be acting downwards along with the weight of the vehicle, and hence impact to the vehicle will be more. This will result in jerking of the vehicle and cause discomfort to the passengers.
Shape of Valley Curve
For gradually introducing and increasing the centrifugal force acting downwards, the best shape that could be given for a valley curve is a transition curve.
Cubic parabola is generally preferred in vertical valley curves.
Length of Valley Curve (IRC Approach)
23The valley curve is made fully transitional by providing two similar transition curves of equal length. The transitional curve is set out by a cubic parabola.
The length of Valley Transition Curve is based on two criteria
A. Comfort or Centrifugal Acceleration Criteria
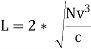
Where,
L: Total Length of Valley Curve
N: Deviation Angle
C: Allowable rate of change of centrifugal acceleration = 0.61 m/s3
B. Safety or Headlight Sight Distance Criteria
While deciding the length of valley curve for headlight distance, two situations can arise depending on the uphill and downhill gradients
When the length of the curve is greater than stopping sight distance (L>S)
When the length of the curve is greater than stopping sight distance. ((L<S)
Case 1: L>S
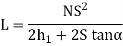
Where,
L: Total Length of Valley Curve
N: Deviation Angle
h1: Height of Headlight = 0.75m
α: Headlight beam angle = 1°
S: Headlight Sight Distance, m
Case 2: L<S
