Unit - 3

Knowledge Representation & Reasoning

Q1) With an example, show objects, properties functions and relations?

A1)

“EVIL KING JOHN BROTHER OF RICHARD RULED ENGLAND IN 1200”

Objects: John, Richard, England, 1200

Relation: Ruled

Properties: Evil, King

Functions: BROTHER OF

Q2) Define an inference procedure?

A2)

An inference procedure reports whether or not a sentence is entitled by knowledge base provided a knowledge base and a sentence. An inference procedure ‘i’ can be described by the sentences that it can derive. If i can derive from knowledge base, we can write. KB --Alpha is derived from KB or i derives alpha from KB.

Q3) Define Propositional logic?

A3)

Propositional logic (PL) is the simplest form of logic where all the statements are made by propositions. A proposition is a declarative statement which is either true or false. It is a technique of knowledge representation in logical and mathematical form.

Example:

1. a) It is Sunday.  
2. b) The Sun rises from West (False proposition)  
3. c) 3+3= 7(False proposition)  
4. d) 5 is a prime number.   

Following are some basic facts about propositional logic:

• Propositional logic is also called Boolean logic as it works on 0 and 1.
• In propositional logic, we use symbolic variables to represent the logic, and we can use any symbol for a representing a proposition, such A, B, C, P, Q, R, etc.
• Propositions can be either true or false, but it cannot be both.
• Propositional logic consists of an object, relations or function, and logical connectives.
• These connectives are also called logical operators.
• The propositions and connectives are the basic elements of the propositional logic.
• Connectives can be said as a logical operator which connects two sentences.
• A proposition formula which is always true is called tautology, and it is also called a valid sentence.
• A proposition formula which is always false is called Contradiction.
• A proposition formula which has both true and false values is called
• Statements which are questions, commands, or opinions are not propositions such as "Where is Rohini", "How are you", "What is your name", are not propositions.

Syntax of propositional logic:

The syntax of propositional logic defines the allowable sentences for the knowledge representation. There are two types of Propositions:

1. Atomic Propositions
2. Compound propositions

Q4) Describe about types of Knowledge representation?

A4)

There are four types of Knowledge representation:

Relational, Inheritable, Inferential, and Declarative/Procedural.

◊ Relational Knowledge:

Provides a framework to compare two objects based on equivalent attributes.

Any instance in which two different objects are compared is a relational type of knowledge.

◊ Inheritable Knowledge

− is obtained from associated objects.

− it prescribes a structure in which new objects are created which may inherit all or a subset of attributes from existing objects.

◊ Inferential Knowledge

− is inferred from objects through relations among objects.

− e.g., a word alone is a simple syntax, but with the help of other

Words in phrase the reader may infer more from a word; this inference within linguistic is called semantics.

◊ Declarative Knowledge

− a statement in which knowledge is specified, but the use to which that knowledge is to be put is not given.

− e.g., laws, people's name; these are facts which can stand alone, not

Dependent on other knowledge;

Procedural Knowledge

− a representation in which the control information, to use the knowledge, is embedded in the knowledge itself.

− e.g., computer programs, directions, and recipes; these indicate specific use or implementation

Q5) Discuss in details about inferential knowledge?

A5)

This knowledge generates new information from the given information.

This new information does not require further data gathering form soue, but does require analysis of the given information to generate new knowledge.

− given a set of relations and values, one may infer other values or relations.

− a predicate logic (a mathematical deduction) is used to infer from a set of attributes.

− inference through predicate logic uses a set of logical operations to relate individual data.

− the symbols used for the logic operations are:

" → " (implication), " ¬ " (not), " V " (or), " Λ " (and),

" ∀ " (for all), " ∃ " (there exists).

Examples of predicate logic statements:

1. "Wonder" is a name of a dog: dog (wonder)

2.All dogs belong to the class of animals: ∀ x: dog (x) → animal(x)

3.All animals either live on land or in ∀ x: animal(x) → live (x, water: land) V live (x, water)

From these three statements we can infer that:

" Wonder lives either on land or on water."

Q6) Discuss about Predicate Logic?

A6)

Predicate Logic

The propositional logic, is not powerful enough for all types of assertions;

Example: The assertion "x > 1", where x is a variable, is not a proposition

Because it is neither true nor false unless value of x is defined.

For x > 1 to be a proposition,

− either we substitute a specific number for x;

− or change it to something like

"There is a number x for which x > 1 holds";

− or "For every number x, x > 1 holds".

Consider example:

“All men are mortal.

Socrates is a man.

Then Socrates is mortal”,

These cannot be expressed in propositional logic as a finite and logically valid argument (formula).

We need languages: that allow us to describe properties (predicates) of objects, or a relationship among objects represented by the variables.

Predicate logic satisfies the requirements of a language.

− Predicate logic is powerful enough for expression and reasoning.

− Predicate logic is built upon the ideas of propositional logic.

Predicate:

Every complete "sentence" contains two parts: a "subject" and a "predicate".

The subject is what (or whom) the sentence is about.

The predicate tells something about the subject;

Example:

A sentence "Judy {runs}".

The subject is Judy and the predicate is runs.

Predicate, always includes verb, tells something about the subject.

Predicate is a verb phrase template that describes a property of objects, or a relation among objects represented by the variables.

Example:

“The car Tom is driving is blue"; "The sky is blue”; "The cover of this book is blue"

Predicate is “is blue”, describes property.

Predicates are given names; Let „B‟ is name for predicate "is_blue".

Sentence is represented as "B(x)", read as "x is blue"; Symbol “x” represents an arbitrary Object.

Q7) Comparison between procedural and declarative language?

A7)

Q8) Define Semantics?

A8)

The semantics of the language defines the truth of each sentence with respect to each possible world. With this semantics, when a particular configuration exists within an agent, the agent believes the corresponding sentence.

Q9) Define Forward chaining?

A9)

Forward chaining is also known as forward deduction or forward reasoning when using an inference engine. Forward chaining is a method of reasoning that begins with atomic sentences in a knowledge base and uses inference rules to extract more information in the forward direction until a goal is reached.

Beginning with known facts, the Forward-chaining algorithm activates all rules with satisfied premises and adds their conclusion to the known facts. This procedure is repeated until the problem is resolved.

It's a method of inference that starts with sentences in the knowledge base and generates new conclusions that may then be utilized to construct subsequent inferences. It's a plan based on data. We start with known facts and organize or chain them to get to the query. The ponens modus operandi is used. It begins with the data that is already accessible and then uses inference rules to extract new data until the goal is achieved.

Example: To determine the color of Fritz, a pet who croaks and eats flies, for example. The Knowledge Base contains the following rules:

If X croaks and eats flies — → Then X is a frog.

If X sings — → Then X is a bird.

If X is a frog — → Then X is green.

If x is a bird — -> Then X is blue.

In the KB, croaks and eating insects are found. As a result, we arrive at rule 1, which has an antecedent that matches our facts. The KB is updated to reflect the outcome of rule 1, which is that X is a frog. The KB is reviewed again, and rule 3 is chosen because its antecedent (X is a frog) corresponds to our newly confirmed evidence. The new result is then recorded in the knowledge base (i.e., X is green). As a result, we were able to determine the pet's color based on the fact that it croaks and eats flies.

Properties of forward chaining

●      It is a down-up approach since it moves from bottom to top.

●      It is a process for reaching a conclusion based on existing facts or data by beginning at the beginning and working one's way to the end.

●      Because it helps us to achieve our goal by exploiting current data, forward-chaining is also known as data-driven.

●      The forward-chaining methodology is often used in expert systems, such as CLIPS, business, and production rule systems.

Q10) Define Backward chaining?

A10)

Backward-chaining is also known as backward deduction or backward reasoning when using an inference engine. A backward chaining algorithm is a style of reasoning that starts with the goal and works backwards through rules to find facts that support it.

It's an inference approach that starts with the goal. We look for implication phrases that will help us reach a conclusion and justify its premises. It is an approach for proving theorems that is goal-oriented.

Example: Fritz, a pet that croaks and eats flies, needs his color determined. The Knowledge Base contains the following rules:

If X croaks and eats flies — → Then X is a frog.

If X sings — → Then X is a bird.

If X is a frog — → Then X is green.

If x is a bird — -> Then X is blue.

The third and fourth rules were chosen because they best fit our goal of determining the color of the pet. For example, X may be green or blue. Both the antecedents of the rules, X is a frog and X is a bird, are added to the target list. The first two rules were chosen because their implications correlate to the newly added goals, namely, X is a frog or X is a bird.

Because the antecedent (If X croaks and eats flies) is true/given, we can derive that Fritz is a frog. If it's a frog, Fritz is green, and if it's a bird, Fritz is blue, completing the goal of determining the pet's color.

Properties of backward chaining

●      A top-down strategy is what it's called.

●      Backward-chaining employs the modus ponens inference rule.

●      In backward chaining, the goal is broken down into sub-goals or sub-goals to ensure that the facts are true.

●      Because a list of objectives decides which rules are chosen and implemented, it's known as a goal-driven strategy.

●      The backward-chaining approach is utilized in game theory, automated theorem proving tools, inference engines, proof assistants, and other AI applications.

●      The backward-chaining method relied heavily on a depth-first search strategy for proof.

Q11) Define skolem constant?

A11)

The existential sentence says there is some object satisfying a condition, and the instantiation process is just giving a name to that object. That name must not belong to another object. The new name is called skolem constant

Q12) What are the divisions of knowledge in OTTER theorem?

A12)

i. Set of Support (SOS)

Ii. Usable axioms

Iii. Rewrites (or) Demodulators

Iv. A set of parameters and sentences

Q13) Define Hidden Markov Models (HMM)?

A13)

The Hidden Markov Model (HMM) is an analytical Model where the system being modelled is considered a Markov process with hidden or unobserved states. Machine learning and pattern recognition applications, like gesture recognition & speech handwriting, are applications of the Hidden Markov Model.

HMM, Hidden Markov Model enables us to speak about observed or visible events and hidden events in our probabilistic model.

The below diagram depicts the interaction between two ‘HIDDEN’ states, ‘Rainy’ and ‘Sunny’ in this case. ‘Walk’, ‘Shop’, and ‘Clean’ in the below diagram are known as data, referred to as OBSERVATIONS

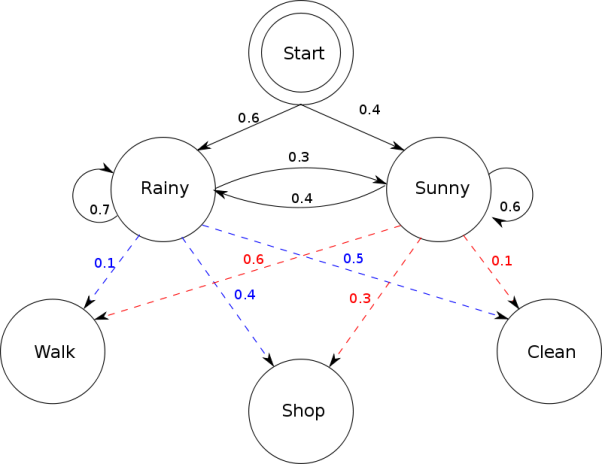
Markov Chain – three states (snow, rain, and sunshine)

P – the transition probability matrix

q – the initial probabilities 

The above example represents the invisible Markov Chain; for instance, we are at home and cannot see the weather. However, we can feel the temperature inside the rooms at home.

There will be two possible observations, hot and cold, where.

P(Hot|Snow) = 0, P(Cold|Snow) = 1

P(Hot|Rain) = 0.2, P(Cold|Rain) = 0.8

P(Hot|Sunshine) = 0.7, P(Cold|Sunshine) = 0.3

Example on HMM to compute the probability of whether we will feel cold for two consecutive days; there are 3*3=9 possibilities or options for the underlying Markov states in these two days.

P((Cold, Cold), P(Rain, Snow)) = P((Cold, Cold)|(Rain, Snow)).P(Rain, Snow) = P(Cold|Rain).P(Cold|Snow).P(Snow|Rain).P(Rain) = 0.8 . 1 . 0.1 . 0.2 = 0.016

Note -The probability will be calculated as the sum of all the possibilities

Q14) Define Bayesian Networks?

A14)

Bayesian belief network is key computer technology for dealing with probabilistic events and to solve a problem which has uncertainty. We can define a Bayesian network as:

"A Bayesian network is a probabilistic graphical model which represents a set of variables and their conditional dependencies using a directed acyclic graph."

It is also called a Bayes network, belief network, decision network, or Bayesian model.

Bayesian networks are probabilistic, because these networks are built from a probability distribution, and also use probability theory for prediction and anomaly detection.

Real world applications are probabilistic in nature, and to represent the relationship between multiple events, we need a Bayesian network. It can also be used in various tasks including prediction, anomaly detection, diagnostics, automated insight, reasoning, time series prediction, and decision making under uncertainty.

Bayesian Network can be used for building models from data and expert’s opinions, and it consists of two parts:

• Directed Acyclic Graph
• Table of conditional probabilities.

The generalized form of Bayesian network that represents and solve decision problems under uncertain knowledge is known as an Influence diagram.

A Bayesian network graph is made up of nodes and Arcs (directed links), where:

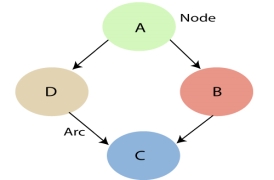
• Each node corresponds to the random variables, and a variable can be continuous or discrete.
• Arc or directed arrows represent the causal relationship or conditional probabilities between random variables. These directed links or arrows connect the pair of nodes in the graph.
  These links represent that one node directly influence the other node, and if there is no directed link that means that nodes are independent with each other
  • In the above diagram, A, B, C, and D are random variables represented by the nodes of the network graph.
  • If we are considering node B, which is connected with node A by a directed arrow, then node A is called the parent of Node B.
  • Node C is independent of node A.

Note: The Bayesian network graph does not contain any cyclic graph. Hence, it is known as a directed acyclic graph or DAG.

The Bayesian network has mainly two components:

• Causal Component
• Actual numbers

Each node in the Bayesian network has condition probability distribution P (Xi |Parent (Xi)), which determines the effect of the parent on that node.

Bayesian network is based on Joint probability distribution and conditional probability. So, let's first understand the joint probability distribution:

Joint probability distribution:

If we have variables x1, x2, x3,....., xn, then the probabilities of a different combination of x1, x2, x3.. Xn, are known as Joint probability distribution.

P[x1, x2, x3,....., xn], it can be written as the following way in terms of the joint probability distribution.

= P[x1| x2, x3,....., xn]P[x2, x3,....., xn]

= P[x1| x2, x3,....., xn]P[x2|x3,....., xn]....P[xn-1|xn]P[xn].

In general, for each variable Xi, we can write the equation as:

P(Xi|Xi-1,........., X1) = P(Xi |Parents(Xi ))

Explanation of Bayesian network:

Let's understand the Bayesian network through an example by creating a directed acyclic graph:

Example: Harry installed a new burglar alarm at his home to detect burglary. The alarm reliably responds at detecting a burglary but also responds for minor earthquakes. Harry has two neighbors David and Sophia, who have taken a responsibility to inform Harry at work when they hear the alarm. David always calls Harry when he hears the alarm, but sometimes he got confused with the phone ringing and calls at that time too. On the other hand, Sophia likes to listen to high music, so sometimes she misses to hear the alarm. Here we would like to compute the probability of Burglary Alarm.

Q15) What do you mean by Logical Connectives?

A15)

Logical connectives are used to connect two simpler propositions or representing a sentence logically. We can create compound propositions with the help of logical connectives. There are mainly five connectives, which are given as follows:

1. Negation: A sentence such as ¬ P is called negation of P. A literal can be either Positive literal or negative literal.
2. Conjunction: A sentence which has ∧connective such as, P ∧ Q is called a conjunction.
   Example: Rohan is intelligent and hardworking. It can be written as,
   P= Rohan is intelligent,
   Q= Rohan is hardworking. → P∧ Q.
3. Disjunction: A sentence which has ∨ connective, such as P ∨ Q. Is called disjunction, where P and Q are the propositions.
   Example: "Ritika is a doctor or Engineer",
   Here P= Ritika is Doctor. Q= Ritika is Doctor, so we can write it as P ∨ Q.
4. Implication: A sentence such as P → Q, is called an implication. Implications are also known as if-then rules. It can be represented as
         If it is raining, then the street is wet.
           Let P= It is raining, and Q= Street is wet, so it is represented as P → Q
5. Biconditional: A sentence such as P⇔ Q is a Biconditional sentence, example If I am breathing, then I am alive
   P= I am breathing, Q= I am alive, it can be represented as P ⇔ Q.

Q16) Explain Precedence of connectives?

A16)

Just like arithmetic operators, there is a precedence order for propositional connectors or logical operators. This order should be followed while evaluating a propositional problem. Following is the list of the precedence order for operators:

First Precedence Parenthesis

Second Precedence Negation

Third Precedence Conjunction(AND)

Fourth Precedence Disjunction(OR)

Fifth Precedence Implication

Six Precedence Biconditional

Note: For better understanding use parenthesis to make sure of the correct interpretations. Such as ¬R∨ Q, it can be interpreted as (¬R) ∨ Q.

Q17) Explain Logical equivalence?

A17)

Logical equivalence is one of the features of propositional logic. Two propositions are said to be logically equivalent if and only if the columns in the truth table are identical to each other.

Let's take two propositions A and B, so for logical equivalence, we can write it as A⇔B. In below truth table we can see that column for ¬A∨ B and A→B, are identical hence A is Equivalent to B

A	B	A	A∨B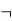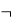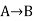
T	T	F	T	T
T	F	F	F	F
F	T	T	T	T
F	F	T	T	T

Properties of Operators:

• Commutativity:
  • P∧ Q= Q ∧ P, or
  • P ∨ Q = Q ∨ P.
• Associativity:
  • (P ∧ Q) ∧ R= P ∧ (Q ∧ R),
  • (P ∨ Q) ∨ R= P ∨ (Q ∨ R)
• Identity element:
  • P ∧ True = P,
  • P ∨ True= True.
• Distributive:
  • P∧ (Q ∨ R) = (P ∧ Q) ∨ (P ∧ R).
  • P ∨ (Q ∧ R) = (P ∨ Q) ∧ (P ∨ R).
• DE Morgan's Law:
  • ¬ (P ∧ Q) = (¬P) ∨ (¬Q)
  • ¬ (P ∨ Q) = (¬ P) ∧ (¬Q).
• Double-negation elimination:
  • ¬ (¬P) = P.

Limitations of Propositional logic:

• We cannot represent relations like ALL, some, or none with propositional logic. Example:
  1. All the girls are intelligent.
  2. Some apples are sweet.
• Propositional logic has limited expressive power.
• In propositional logic, we cannot describe statements in terms of their properties or logical relationships.

Q18) What do you mean by Generalized Modus Ponens Rule?

A18)

For the inference process in FOL, we have a single inference rule which is called Generalized Modus Ponens. It is lifted version of Modus ponens.

Generalized Modus Ponens can be summarized as, " P implies Q and P is asserted to be true, therefore Q must be True."

According to Modus Ponens, for atomic sentences pi, pi', q. Where there is a substitution θ such that SUBST (θ, pi',) = SUBST (θ, pi), it can be represented as:

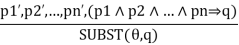
Example:

We will use this rule for Kings are evil, so we will find some x such that x is king, and x is greedy so we can infer that x is evil.

1. Here let say, p1' is king(John)        p1 is king(x)  
2. p2' is Greedy(y)                       p2 is Greedy(x)  
3. θ is {x/John, y/John}                  q is evil(x)  
4. SUBST(θ, q).                                                        

Q19) Define a Proof?

A19)

A sequence of application of inference rules is called a proof. Finding proof is exactly finding solution to search problems. If the successor function is defined to generate all possible applications of inference rules, then the search algorithms can be applied to find proofs.

Q20) Define the Following?

1.     Complete inference procedure

2.     Interpretation

3.     Validity of a sentence

A20)

1. An inference procedure is complete if it can derive all true conditions from a set of premises.
2. Interpretation specifies exactly which objects, relations and functions are referred to by the constant predicate, and function symbols.
3. A sentence is valid or necessarily true if and only if it is true under all possible interpretation in all possible world