Unit - 4

Machine Learning

Q1) Differentiate Supervised and Unsupervised learning?

A1)

Q2) What is meant by belief network?

A2)

A belief network is a graph in which the following holds

A set of random variables

A set of directive links or arrows connects pairs of nodes.

The conditional probability table for each node

The graph has no directed cycles.

Q3) Give the Baye's rule equation

A3)

W.K.T P (A ^ B) = P(A/B) P(B) -------------------------- 1

P (A ^ B) = P(B/A) P(A) -------------------------- 2

DIVIDING BY P(A);

WE GET

P(B/A) = P(A/B) P(B) -------------------- P(A)

Q4) Mention the exercises which broaden the applications of decision trees.?

A4)

i. Missing data

Ii. Multivalued attributes

Iii. Continuous and integer valued input attributes

Iv. Continuous valued output attributes.

Q5) Define RBL.?

A5)

Relevance based Learning; the prior knowledge background concerns the relevance of a set of

Features to the goal predicate. This knowledge together with the observations,

Allows the agent to infer a new, general rule that explains the observations.

Hypothesis ^ Description |= classifications,

Background ^ Description ^ classifications |= Hypothesis

Q6) What is the basic EBL process step?

A6)

i. Construct a proof using the available background knowledge.

Ii. Construct a generalized proof tree for the variabilized goal using the same inference steps as in the original proof.

Iii. Construct a new rule where LHS consists of the leaves of the proof tree and R.H.S is the variabilized goal.

Iv. Drop any conditions that are true

Q7) What are the components of planning system and explain in detail?

A7)

Reasoning is the act of deriving a conclusion from certain premises using a given methodology.

• Reasoning is a process of thinking; reasoning is logically arguing; reasoning is drawing inference.

• When a system is required to do something, that it has not been explicitly told how to do, it must reason. It must figure out what it needs to know from what it already knows.

• Many types of Reasoning have long been identified and recognized, but many questions regarding their logical and computational properties still remain controversial.

• The popular methods of Reasoning include abduction, induction, model based, explanation and confirmation. All of them are intimately related to problems of belief revision and theory development, knowledge assimilation, discovery and learning.

A formal language may be viewed as being analogous to of words or a collection of sentences.

AI – Reasoning: a collection

In computer science, a formal language is defined by precise mathematical or machine process able formulas.

‡ A formal language L is characterized as a set F of finite-length sequences of elements drawn from a specified finite set A of symbols.

‡ Mathematically, it is an unordered pair L = {A, F}

‡ If A is words, then the set A is called alphabet of L, and the elements of F are called words.

‡ If A is sentence, then the set A is called the lexicon or vocabulary of F, and the elements of F are then called sentences.

‡ The mathematical theory that treats formal languages in general is known as formal language theory.

Q8) List out the different Methods of Reasoning?

A8)

Mostly three kinds of logical reasoning: Deduction, Induction, Abduction.

■ Deduction

‡ Example: "When it rains, the grass gets wet. It rains. Thus, the grass is wet."

This means in determining the conclusion; it is using rule and its precondition to make a conclusion.

‡ Applying a general principle to a special case.

‡ Using theory to make predictions

‡ Usage: Inference engines, Theorem provers, Planning.

■ Induction

‡ Example: "The grass has been wet every time it has rained. Thus, when it rains, the grass gets wet."

This means in determining the rule; it is learning the rule after numerous examples of conclusion following the precondition.

‡ Deriving a general principle from special cases

‡ From observations to generalizations to knowledge

‡ Usage: Neural nets, Bayesian nets, Pattern recognition

Get useful study materials from www.rejinpaul.com

■ AI - Reasoning

Abduction

‡ Example: "When it rains, the grass gets wet. The grass is wet, it must have rained."

Means determining the precondition; it is using the conclusion and the rule to support that the precondition could explain the conclusion.

‡ Guessing that some general principle can relate a given pattern of cases

‡ Extract hypotheses to form a tentative theory

‡ Usage: Knowledge discovery, Statistical methods, Data mining.

■ Analogy

‡ Example: "An atom, with its nucleus and electrons, is like the solar system, with its sun and planets."

Means analogous; it is illustration of an idea by means of a more familiar idea that is similar to it in some significant features. And thus, said to be analogous to it.

‡ Finding a common pattern in different cases

‡ Usage: Matching labels, Matching sub-graphs, Matching transformations.

Note: Deductive reasoning and Inductive reasoning are the two most commonly used explicit methods of reasoning to reach a conclusion.

Q9) Describe Bayes’ Theorem?

A9)

Bayesian view of probability is related to degree of belief.

It is a measure of the plausibility of an event given incomplete knowledge.

Bayes' theorem is also known as Bayes' rule or Bayes' law, or called Bayesian reasoning.

The probability of an event A conditional on another event B i.e., P(A|B) is generally different from probability of B conditional on A i.e., P(B|A).

There is a definite relationship between the two, P(A|B) and P(B|A), and Bayes' theorem is the statement of that relationship.

Bayes theorem is a way to calculate P(A|B) from a knowledge of P(B|A).

Bayes' Theorem is a result that allows new information to be used to update the conditional probability of an event

Bayes’ Theorem

Let S be a sample space.

Let A1, A2,…,An be a set of mutually exclusive events from S.

Let B be any event from the same S, such that P(B)>0

Then Bayes’ Theorem describes following two probabilities:

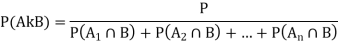
And by invoking the fact 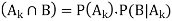the probability

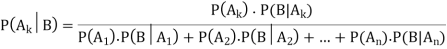
Applying Bayes’ Theorem:

Bayes’ theorem is applied while following conditions exist.

The sample space S is portioned into a set of mutually exclusive events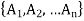

Bayes’ theorem is applied while following conditions exist.

• The sample space S is partitioned into a set of mutually exclusive events
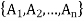
• Within s, there exists an event B, for which
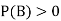
• The goal is to compute a conditional probability of the form:
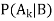
• You know at least one of the two sets probabilities described below 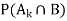for each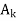

Q10) Discuss in details about Rule Based Systems?

A10)

A rule is an expression of the form "if A then B" where

1. A is an assertion and B can be either an action or another assertion.
2. Example: Trouble shooting of water pumps
3. If pump failure then the pressure is low
4. If pump failure then check oil level
5. If power failure then pump failure
6. Rule based system insists of a library of such rules.
7. Rules reflect essential relationships within the domain.
8. Rules reflect ways to reason about the domain.
9. Rules draw conclusions and points to actions, when specific information about the domain comes in. This is called inference.
10. The inference is a kind of chain reaction like: If there is a power failure then (see rules 1, 2, 3 mentioned above)
11. Rule 3 states that there is a pump failure, and Rule 1 tells that the pressure is low, and
12. Rule 2 gives a (useless) recommendation to check the oil level.

It is very difficult to control such a mixture of inference back and forth in the same session and resolve such uncertainties.

Q11) Explain in details about Bayesian Network?

A11)

Bayesian belief network is key computer technology for dealing with probabilistic events and to solve a problem which has uncertainty. We can define a Bayesian network as:

"A Bayesian network is a probabilistic graphical model which represents a set of variables and their conditional dependencies using a directed acyclic graph."

It is also called a Bayes network, belief network, decision network, or Bayesian model.

Bayesian networks are probabilistic, because these networks are built from a probability distribution, and also use probability theory for prediction and anomaly detection.

Real world applications are probabilistic in nature, and to represent the relationship between multiple events, we need a Bayesian network. It can also be used in various tasks including prediction, anomaly detection, diagnostics, automated insight, reasoning, time series prediction, and decision making under uncertainty.

Bayesian Network can be used for building models from data and experts’ opinions, and it consists of two parts:

Directed Acyclic Graph

Table of conditional probabilities.

The generalized form of Bayesian network that represents and solve decision problems under uncertain knowledge is known as an Influence diagram.

A Bayesian network graph is made up of nodes and Arcs (directed links), where:

• Each node corresponds to the random variables, and a variable can be continuous or discrete.
• Arc or directed arrows represent the causal relationship or conditional probabilities between random variables. These directed links or arrows connect the pair of nodes in the graph.
  These links represent that one node directly influence the other node, and if there is no directed link that means that nodes are independent with each other

In the above diagram, A, B, C, and D are random variables represented by the nodes of the network graph.

If we are considering node B, which is connected with node A by a directed arrow, then node A is called the parent of Node B.

Node C is independent of node A.

Note: The Bayesian network graph does not contain any cyclic graph. Hence, it is known as a directed acyclic graph or DAG.

The Bayesian network has mainly two components:

Causal Component

Actual numbers

Each node in the Bayesian network has condition probability distribution P(Xi |Parent(Xi) ), which determines the effect of the parent on that node.

Bayesian network is based on Joint probability distribution and conditional probability. So, let's first understand the joint probability distribution:

Joint probability distribution:

If we have variables x1, x2, x3,....., xn, then the probabilities of a different combination of x1, x2, x3.. Xn, are known as Joint probability distribution.

P[x1, x2, x3,....., xn], it can be written as the following way in terms of the joint probability distribution.

= P[x1| x2, x3,....., xn]P[x2, x3,....., xn]

= P[x1| x2, x3,....., xn]P[x2|x3,....., xn]....P[xn-1|xn]P[xn].

In general, for each variable Xi, we can write the equation as:

P(Xi|Xi-1,........., X1) = P(Xi |Parents(Xi ))

Explanation of Bayesian network:

Let's understand the Bayesian network through an example by creating a directed acyclic graph:

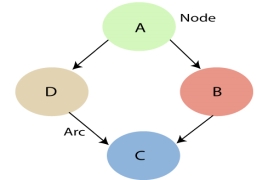
Example: Harry installed a new burglar alarm at his home to detect burglary. The alarm reliably responds at detecting a burglary but also responds for minor earthquakes. Harry has two neighbors David and Sophia, who have taken a responsibility to inform Harry at work when they hear the alarm. David always calls Harry when he hears the alarm, but sometimes he got confused with the phone ringing and calls at that time too. On the other hand, Sophia likes to listen to high music, so sometimes she misses to hear the alarm. Here we would like to compute the probability of Burglary Alarm.

Problem:

Calculate the probability that alarm has sounded, but there is neither a burglary, nor an earthquake occurred, and David and Sophia both called the Harry.

Solution:

• The Bayesian network for the above problem is given below. The network structure is showing that burglary and earthquake is the parent node of the alarm and directly affecting the probability of alarm's going off, but David and Sophia's calls depend on alarm probability.
• The network is representing that our assumptions do not directly perceive the burglary and also do not notice the minor earthquake, and they also not confer before calling.
• The conditional distributions for each node are given as conditional probabilities table or CPT.
• Each row in the CPT must be sum to 1 because all the entries in the table represent an exhaustive set of cases for the variable.
• In CPT, a boolean variable with k boolean parents contains 2K probabilities. Hence, if there are two parents, then CPT will contain 4 probability values

List of all events occurring in this network:

Burglary (B)

Earthquake(E)

Alarm(A)

David Calls(D)

Sophia calls(S)

We can write the events of problem statement in the form of probability: P[D, S, A, B, E], can rewrite the above probability statement using joint probability distribution:

P[D, S, A, B, E]= P[D | S, A, B, E]. P[S, A, B, E]

=P[D | S, A, B, E]. P[S | A, B, E]. P[A, B, E]

= P [D| A]. P [ S| A, B, E]. P[ A, B, E]

= P[D | A]. P[ S | A]. P[A| B, E]. P[B, E]

= P[D | A ]. P[S | A]. P[A| B, E]. P[B |E]. P[E]

Let's take the observed probability for the Burglary and earthquake component:

P(B= True) = 0.002, which is the probability of burglary.

P(B= False)= 0.998, which is the probability of no burglary.

P(E= True)= 0.001, which is the probability of a minor earthquake

P(E= False)= 0.999, Which is the probability that an earthquake not occurred.

We can provide the conditional probabilities as per the below tables:

Conditional probability table for Alarm A:

The Conditional probability of Alarm A depends on Burglar and earthquake:

Conditional probability table for David Calls:

The Conditional probability of David that he will call depends on the probability of Alarm.

Conditional probability table for Sophia Calls:

The Conditional probability of Sophia that she calls is depending on its Parent Node "Alarm."

From the formula of joint distribution, we can write the problem statement in the form of probability distribution:

P(S, D, A, ¬B, ¬E) = P (S|A) *P (D|A)*P (A|¬B ^ ¬E) *P (¬B) *P (¬E).

= 0.75* 0.91* 0.001* 0.998*0.999

= 0.00068045.

Hence, a Bayesian network can answer any query about the domain by using Joint distribution.

The semantics of Bayesian Network:

There are two ways to understand the semantics of the Bayesian network, which is given below:

1. To understand the network as the representation of the Joint probability distribution.

It is helpful to understand how to construct the network.

2. To understand the network as an encoding of a collection of conditional independence statements.

It is helpful in designing inference procedure.

Q12) Describe in details about Fuzzy Logic?

A12)

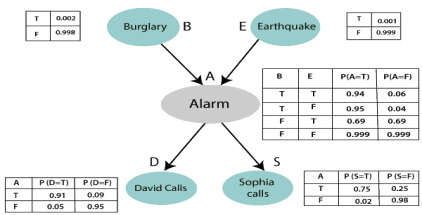
Fuzzy logic was suggested by Zadeh as a method for mimicking the ability of human reasoning using a small number of rules and still producing a smooth output via a process of interpolation.

Description of Fuzzy logic

With fuzzy logic an element could partially belong to a set represented by the set membership. Example, a person of height 1.79 m would belong ot both tall and not of tall sets with a particular degree of membership.

Difference between binary logic and fuzzy logic

• A fuzzy logic system is one that has at least one system component that uses fuzzy logic for its internal knowledge representation.
• Fuzzy system communicates information using fuzzy sets.
• Fuzzy logic is used purely for internal knowledge representation and externally it can be considered as any other system component.

Q13) Define Decision trees?

A13)

Decision Tree is a Supervised learning technique that can be used for both classification and Regression problems, but mostly it is preferred for solving Classification problems. It is a tree-structured classifier, where internal nodes represent the features of a dataset, branches represent the decision rules and each leaf node represents the outcome.

• In a Decision tree, there are two nodes, which are the Decision Node and Leaf Node. Decision nodes are used to make any decision and have multiple branches, whereas Leaf nodes are the output of those decisions and do not contain any further branches.
• The decisions or the test are performed on the basis of features of the given dataset.
• It is a graphical representation for getting all the possible solutions to a problem/decision based on given conditions.
• It is called a decision tree because, similar to a tree, it starts with the root node, which expands on further branches and constructs a tree-like structure.
• In order to build a tree, we use the CART algorithm, which stands for Classification and Regression Tree algorithm.
• A decision tree simply asks a question, and based on the answer (Yes/No), it further split the tree into subtrees.
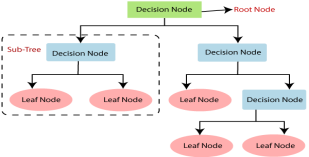
• Below diagram explains the general structure of a decision tree:

Note: A decision tree can contain categorical data (YES/NO) as well as numeric data.

Why use Decision Trees?

There are various algorithms in Machine learning, so choosing the best algorithm for the given dataset and problem is the main point to remember while creating a machine learning model. Below are the two reasons for using the Decision tree:

• Decision Trees usually mimic human thinking ability while making a decision, so it is easy to understand.
• The logic behind the decision tree can be easily understood because it shows a tree-like structure.

Decision Tree Terminologies

1. Root Node: Root node is from where the decision tree starts. It represents the entire dataset, which further gets divided into two or more homogeneous sets.
2. Leaf Node: Leaf nodes are the final output node, and the tree cannot be segregated further after getting a leaf node.
3. Splitting: Splitting is the process of dividing the decision node/root node into sub-nodes according to the given conditions.
4. Branch/Sub Tree: A tree formed by splitting the tree.
5. Pruning: Pruning is the process of removing the unwanted branches from the tree.
6. Parent/Child node: The root node of the tree is called the parent node, and other nodes are called the child nodes

Q14) What do you mean by Statistical learning models?

A14) Statistical Learning is a set of tools for understanding data. These tools broadly come under two classes: supervised learning & unsupervised learning. Generally, supervised learning refers to predicting or estimating an output based on one or more inputs.

Unsupervised learning, on the other hand, provides a relationship or finds a pattern within the given data without a supervised output.

Let, suppose that we observe a response Y and p different predictors X = (X₁, X₂,…., Xp). In general, we can say:

Y =f(X) + ε

Here f is an unknown function, and ε is the random error term.

In essence, statistical learning refers to a set of approaches for estimating f.

In cases where we have set of X readily available, but the output Y, not so much, the error averages to zero, and we can say:

¥ = ƒ(X)

Where ƒ represents our estimate of f and ¥ represents the resulting prediction.

Hence for a set of predictors X, we can say:

E(Y — ¥)² = E[f(X) + ε — ƒ(X)]²=> E(Y — ¥)² = [f(X) - ƒ(X)]² + Var(ε)

Where,

• E(Y — ¥)² represents the expected value of the squared difference between actual and expected result.
• [f(X) — ƒ(X)]² represents the reducible error. It is reducible because we can potentially improve the accuracy of ƒ by better modeling.
• Var(ε) represents the irreducible error. It is irreducible because no matter how well we estimate ƒ, we cannot reduce the error introduced by variance in ε.

Examples of where statistical methods are used in an applied machine learning project.

1. Problem Framing: Requires the use of exploratory data analysis and data mining.
2. Data Understanding: Requires the use of summary statistics and data visualization.
3. Data Cleaning. Requires the use of outlier detection, imputation and more.
4. Data Selection. Requires the use of data sampling and feature selection methods.
5. Data Preparation. Requires the use of data transforms, scaling, encoding and much more.
6. Model Evaluation. Requires experimental design and re sampling methods.
7. Model Configuration. Requires the use of statistical hypothesis tests and

Estimation statistics.

Q15) Write the Advantages and Disadvantage of Naive Bayes Classifier?

A15) Advantages of Naive Bayes Classifier:

• Naive Bayes is one of the fast and easy ML algorithms to predict a class of datasets.
• It can be used for Binary as well as Multi-class Classifications.
• It performs well in multi-class predictions as compared to the other Algorithms.
• It is the most popular choice for text classification problems.

Disadvantages of Naive Bayes Classifier:

• Naive Bayes assumes that all features are independent or unrelated, so it cannot learn the relationship between features.

Q16) Explain various types of   Naive Bayes Model?

A16) There are three types of Naive Bayes Model, which are given below.

• Gaussian: The Gaussian model assumes that features follow a normal distribution. This means if predictors take continuous values instead of discrete, then the model assumes that these values are sampled from the Gaussian distribution.
• Multinomial: The Multinomial Naive Bayes classifier is used when the data is multinomial distributed. It is primarily used for document classification problems, it means a particular document belongs to which category such as Sports, Politics, education, etc.
  The classifier uses the frequency of words for the predictors.
• Bernoulli: The Bernoulli classifier works similar to the Multinomial classifier, but the predictor variables are the independent Booleans variables. Such as if a particular word is present or not in a document. This model is also famous for document classification tasks.

Q17) Write EM Algorithm?

A17)

a. Wants to find θ to maximize PRD(θ)

To find theta (θ) that maximizes the probability of data for given θ

b. Instead find θ, 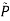to maximize, wher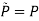e tilde

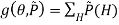log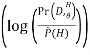

Where 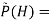Probability distribution over hidden variables, H=Hidden Variables

c. Find Optimum value for g

• Holding θ fixed and optimizing
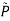
• Holding 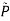fixed and optimizing θ
• And repeat the procedure over and over again

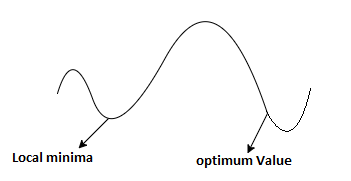
d. g has some local and global optima as PR(D/θ)

e. Example

i. Pick initial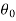

Ii. Probability of hidden variables given the observed data and the current model.

Loop until it converges

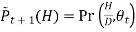
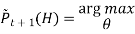
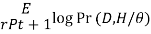
We find the maximum likelihood model for the “expected data” using the distribution over H to generate expected counts for different case.

Iii. Increasing likelihood.

Iv.   Convergence is determined (but difficult)

v.     Process with local optima i.e., sometime it converges quite effectively to the maximum model that’s near the one it started with, but there’s much better model somewhere else in the space.

Q18) Explain Reinforcement learning?

A18) Reinforcement is feedback from which the agent comes to know that something good has happened when it wins and that something bad has happened when it loses. This is also called as reward.

For Example:

In chess game, the reinforcement is received only at the end of the game.

In ping-pong, each point scored can be considered a reward; when learning to crawl, any forward motion is an achievement.

The framework for agents regards the reward as part of the input percept, but the agent must be hardwired to recognize that part as a reward rather than as just another sensory input.

Rewards served to define optimal policies in Markov decision processes.

An optimal policy is a policy that maximizes the expected total reward.

The task of reinforcement learning is to use observed rewards to learn an optimal policy for the environment.

Learning from these reinforcements or rewards is known as reinforcement learning

In reinforcement learning an agent is placed in an environment, the following are the agents.

1. Utility-based agent
2. Q-Learning agent
3. Reflex agent

The following are the types of Reinforcement Learning:

Passive Reinforcement Learning

In this learning, the agent’s policy is fixed and the task is to learn the utilities of states.

• It could also involve learning a model of the environment.
• In passive learning, the agent’s policy 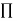is fixed(i.e.) in state s, it always executes the action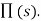
• Its goal is simply to learn the utility function
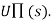
• For example: Consider the 4×3 world.
• The following table shows the policy for that world.

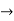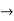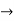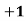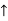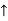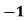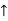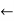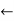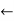The following table shows the corresponding utilities

• Clearly, the passive learning task is similar to the policy evaluation task.
• The main difference is that the passive learning agent does not know
• Neither the transition model T (s, a, s*), which specifies the probability of reaching states from state’s after doing action a:
• Nor does it know the reward function R(s), which specifies the reward for each state.
• The agent executes a set of trials in the environment using its policy
• In each trial, the agent starts in state (1,1) and experiences a sequence of state transitions until it reaches one of the terminal states (4,2) or (4,3)
• Its percept’s supply both current state and the reward received in the state.
• Typical trials might look like this:

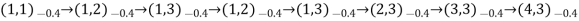
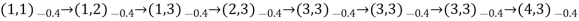
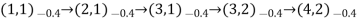
• Note that each state percept is subscripted with the reward received.
• The object is to use the information about rewards to learn the expected utility 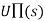associated with each nonterminal state s.
• The utility is defined ot be the expected sum of (discounted rewards obtained if policy is 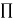followed, the utility function is written as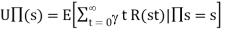
• 
• For the 4×3 world set =1

Active Reinforcement Learning

• A passive learning agent has a fixed policy that determine its behaviour
• “An active agent must decide what actions to do”
• An ADP agent can be taken an considered how it must be modified to handle this new freedom.
• The following are the required modifications:

• First the agent will need to learn a complete model with outcome probabilities for an action. The simple learning mechanism used by PASSIVE-ADP-AGENT will do just fine for this.
• Next, take into account the fact that the agent has a choice of actions. The utilities it needs to learn are those defined by the optimal policy

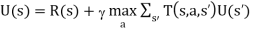
• These equations can be solved to obtain the utility function U using he value iteration or policy algorithms.
• Having obtained a utility fucntion U that is optimal for the learned model, the agent can extract an optimal action by one-step look ahead to maximize the expected utility;
• Alternatively, if it uses policy iteration, the optimal policy is already available, so it should simply execute the action the optimal policy recommends.

Q19) What is Active Reinforcement Learning?

A19)

• A passive learning agent has a fixed policy that determine its behaviour
• “An active agent must decide what actions to do”
• An ADP agent can be taken an considered how it must be modified to handle this new freedom.
• The following are the required modifications:

• First the agent will need to learn a complete model with outcome probabilities for an action. The simple learning mechanism used by PASSIVE-ADP-AGENT will do just fine for this.
• Next, take into account the fact that the agent has a choice of actions. The utilities it needs to learn are those defined by the optimal policy

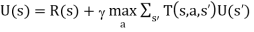
• These equations can be solved to obtain the utility function U using he value iteration or policy algorithms.
• Having obtained a utility fucntion U that is optimal for the learned model, the agent can extract an optimal action by one-step look ahead to maximize the expected utility;
• Alternatively, if it uses policy iteration, the optimal policy is already available, so it should simply execute the action the optimal policy recommends.