Q1) State the principle of operation of a carry look-ahead adder.

A1)

The input carry needed by a stage is directly computed from carry signals obtained from all the preceding stages i-1, i-2…..0, rather than waiting for normal carries to supply slowly from stage to stage. An adder that uses this principle is called carry look-ahead adder.

Q2) What are the main features of Booth’s algorithm?

A2)

1) It handles both positive and negative multipliers uniformly.

2) It achieves some efficiency in the number of addition required when the multiplier has a few large blocks of 1s.

Q3) How can we speed up the multiplication process?

A3)

There are two techniques to speed up the multiplication process:

1) The first technique guarantees that the maximum number of summands that must be added is n/2 for n-bit operands.

2) The second technique reduces the time needed to add the summands.

A4) What is bit pair recoding? Give an example.

A4)

Bit pair recoding halves the maximum number of summands. Group the Booth-recoded multiplier bits in pairs and observe the following: The pair (+1 -1) is equivalent to the pair (0 +1). That is instead of adding -1 times the multiplicand m at shift position i to +1 (M at position i+1, the same result is obtained by adding +1 (M at position i.

E.g.: 11010 – Bit Pair recoding value is 0 -1 -2

Q4) What is the advantage of using Booth algorithm?

A5)

1) It handles both positive and negative multiplier uniformly.

2) It achieves efficiency in the number of additions required when the multiplier has a few large blocks of 1’s.

3) The speed gained by skipping 1’s depends on the data.

Q5) Write the algorithm for restoring division.

A6)

Do the following for n times:

1) Shift A and Q left one binary position.

2) Subtract M and A and place the answer back in A.

3) If the sign of A is 1, set q0 to 0 and add M back to A.

Where A- Accumulator, M- Divisor, Q- Dividend.

Q6) Write the algorithm for non-restoring division.

A7)

Do the following for n times:

Step 1: Do the following for n times:

1) If the sign of A is 0, shift A and Q left one bit position and subtract M from A; otherwise, shift A and Q left and add M to A.

2) Now, if the sign of A is 0, set q0 to 1; otherwise, set q0 to0.

Step 2: if the sign of A is 1, add M to A.

Q7) When can you say that a number is normalized?

A8)

When the decimal point is placed to the right of the first (nonzero) significant digit, the number is said to be normalized.

Q8) Explain about the special values in floating point numbers.

A9)

The end values 0 to 255 of the excess-127 exponent E (are used to represent special values such as:

When E (= 0 and the mantissa fraction M is zero the value exact 0 is represented.

When E (= 255 and M=0, the value (is represented.

When E (= 0 and M (0, denormal values are represented.

When E (= 2555 and M (0, the value represented is called Not a number.

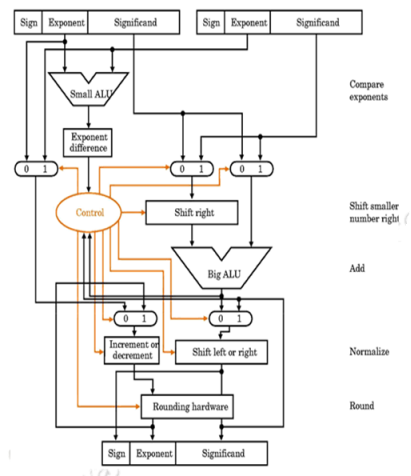
Q9) Write the Add/subtract rule for floating point numbers.

A10)

1) Choose the number with the smaller exponent and shift its mantissa right a number of steps equal to the difference in exponents.

2) Set the exponent of the result equal to the larger exponent.

3) Perform addition/subtraction on the mantissa and determine the sign of the result

4) Normalize the resulting value, if necessary.

Q10) Write the multiply rule for floating point numbers.

A11)

1) Add the exponent and subtract 127.

2) Multiply the mantissa and determine the sign of the result.

3) Normalize the resulting value, if necessary.

Q11) What is the purpose of guard bits used in floating point arithmetic

A12)

Although the mantissa of initial operands are limited to 24 bits, it is important to retain extra bits, called as guard bits.

Q12) What are the ways to truncate the guard bits?

A13)

There are several ways to truncate the guard bits:

1) Chopping

2) Von Neumann rounding

3) Rounding

Q13) Define carry save addition (CSA) process.

A14)

Instead of letting the carries ripple along the rows, they can be saved and introduced into the next roe at the correct weighted position. Delay in CSA is less than delay through the ripple carry adder.

Q14) What are generate and propagate function?

A15)

The generate function is given by

Gi=xiyi    and

The propagate function is given as

Pi=xi+yi.

Q15) What is floating point numbers?

A16)

In some cases, the binary point is variable and is automatically adjusted as computation proceeds. In such case, the binary point is said to float and the numbers are called floating point numbers.

Q16) In floating point numbers when so you say that an underflow or overflow has occurred?

A17)

In single precision numbers when an exponent is less than -126 then we say that an underflow has occurred. In single precision numbers when an exponent is less than +127 then we say that an overflow has occurred.

Q17) What are the difficulties faced when we use floating point arithmetic?

A18)

Mantissa overflow: The addition of two mantissas of the same sign may result in a carryout of the most significant bit

Mantissa underflow: In the process of aligning mantissas, digits may flow off the right end of the mantissa.

Exponent overflow: Exponent overflow occurs when a positive exponent exceeds the maximum possible value.

Exponent underflow: It occurs when a negative exponent exceeds the maximum possible exponent value.

Q18) In conforming to the IEEE standard mention any four situations under which a processor sets exception flag.

A19)

Underflow: If the number requires an exponent less than -126 or in a double precision, if the number requires an exponent less than -1022 to represent its normalized form the underflow occurs.

Overflow: In a single precision, if the number requires an exponent greater than -127 or in a double precision, if the number requires an exponent greater than +1023 to represent its normalized form the underflow occurs.

Divide by zero: It occurs when any number is divided by zero.

Invalid: It occurs if operations such as 0/0 are attempted.

Q19) Why floating-point number is more difficult to represent and process than integer?

A20)

An integer value requires only half the memory space as an equivalent. IEEE double-precision floating point value. Applications that use only integer-based arithmetic will therefore also have significantly smaller memory requirement

A floating-point operation usually runs hundreds of times slower than an equivalent integer based arithmetic operation.

Q20) Give the booth’s recoding and bit-pair recoding of the computer.

1000111101000101

A21)

Booth’s recoding

1     0     0      0    1     1     1     1     0     1     0     0     0      1      0     1     0

-1     0     0    +1     0    0     0    -1   +1    -1     0     0    +1   -1    +1    -1 

Bit-Pair recoding:

1     0     0      0    1     1     1     1     0     1     0     0     0      1      0     1     0

-2            +1         0            -1           +1          0             +1           1

Q21) Draw the full adder circuit and give the truth table?

A22)

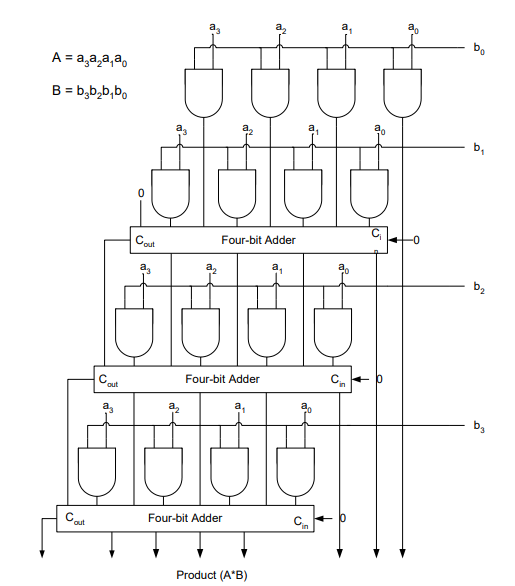
Q22) Define Array Multiplier?

A23)

An array multiplier is a digital combinational circuit used for multiplying two binary numbers by employing an array of full adders and half adders. This array is used for the nearly simultaneous addition of the various product terms involved. To form the various product terms, an array of AND gates is used before the Adder array.

Array multiplier is well known due to its regular structure. Multiplier circuit is based on add and shift algorithm. Each partial product is generated by the multiplication of the multiplicand with one multiplier bit. The partial product is shifted according to their bit orders and then added. The addition can be performed with normal carry propagate adder. N-1 adders are required where N is the multiplier length.

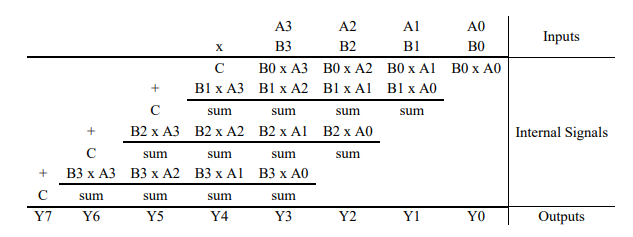
An example of 4-bit multiplication method is shown below:

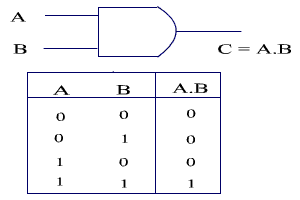
Q23) Define AND, OR and XOR gate?

A24)

AND

The AND logic operation returns true only if either of its inputs are true. If either of the inputs is false, the output is also false.

OR

The OR logic operation returns true if either of its inputs are true. If all inputs are false, the output is also false.

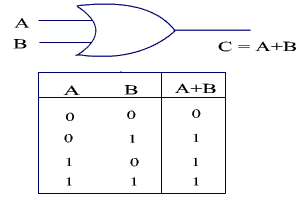
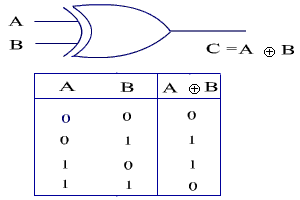
XOR

The XOR logic operation (which stands for "Exclusive OR”) returns true if either of its inputs differ, and false if they are all the same. In other words, if its inputs are a combination of true and false, the output of XOR is true. If its inputs are all true or all false, the output of XOR is false.

Q24) Define organization of a floating-point adder unit?

A25)

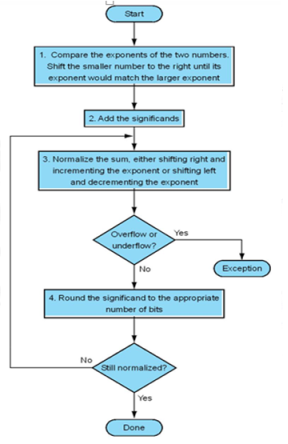
The floating-point multiplication algorithm is given below. A similar algorithm based on the steps discussed before can be used for division.