Unit - 2
Algebraic Structures
Q1) What is algebraic structure?
A1) An algebraic structure is a non-empty set G that contains one or more binary operations. Let's pretend that * is a binary operation on G. The structure (G, *) is then algebraic. The algebraic structure is represented by (N, *), (1, +), and (1, -). (R, +,.) is an algebraic structure with two operations in this case.
Property of algebraic structure
A property of an algebraic structure is one that any of its operations possesses. The following are some of the most important properties of an algebraic system:
1. Associative and commutative laws
If any of the members a, b, c in S meet the associative law, then an operation * on the set is said to be associative or to satisfy the associative law (a * b) * c = a * (b * c).
If a * b = b * a for any element a, b in S, the operation * is said to be commutative or meet the commutative law.
2. Identity element and inverse
Consider the following operation * on the set S. If any element an in S - a * e = e * a = a, an element e in S is called an identity element.
A left identity or a right identity for an element e is defined as e *a or a * e = a, where an is any element in S.
Let's pretend that an operation * on a set S has an identity element e. An element b is the inverse of an element in S, such that a * b = b * a = e.
3. Cancellation laws
If a * b = a * c implies b = c, an operation * on a set S is said to meet the left cancellation law, and if b * a = c * an implies b = c, it is said to satisfy the right cancellation law.
Q2) What do you understand by groups?
A2) A group is an algebraic structure (G, *) in which the binary operation * on G satisfies the following conditions:
Condition-1: For all a, b, c, ∈G
a* (b * c) = (a * b) * c (associativity)
Condition-2: There exists an elements e ∈G such that for any a ∈G
a* e= e * a = a (existence of identity)
Condition-3: For every a ∈G, there exists an element denoted by 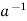 in G such that
in G such that
a* 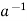 =
= 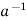 * a = e
* a = e
 is called the inverse of a in G.
is called the inverse of a in G.
Example: (Z, +) is a group where Z denote the set of integers.
Example: (R, +) is a group where R denote the set of real numbers.
Q3) Define subgroup and order?
A3) H is a subgroup of G if a non-void subset H of a group G is itself a group under the operation of G.
Theorem: A group G's subset H is a subgroup of G if and only if:
● a∈ H is the identity element.
● H is closed under G, i.e., if a, b ∈ H, then a, b H, and
● H is closed under inverses, i.e., if an H, then a-1 ∈H.
Cyclic subgroup
A cyclic subgroup K of a group G exists if an element x ∈ G exists such that every element of K can be expressed in the form xn for some n ∈Z.
The element x is referred to as the K generator, and we write K= <x>.
Order
The number of components in the group G determines its order. |G| is the symbol for it. Only the identity element, (e *), is present in an order 1 group.
A group of order 2 consists of two members, one of which is the identity element and the other of which is some other element.
Example 1: Consider the order 2 group (e, x, *). The operation table is displayed.
* | e | x |
e | e | x |
x | x | e |
Three items make up the order 3 group: one identity element and two other elements.
Q4) Explain a cyclic graph?
A4) A cyclic group is one that can be made up of only one element. Every member of a cyclic group is a power of a generator, which is a specific element. A generator 'g' can create a cyclic group in which every other element of the group can be represented as a power of the generator 'g'.
When G=, we say that G is cyclic and that x is a generator of G. That is, if there is an element x ∈ G such that every element of G can be written in the form xn for any n ∈ Z, the group G is said to be cyclic.
Under ordinary multiplication, the group G=1, -1, i, -i is a finite cyclic group with I as generator, thus i1=i, i2=-1, i3=-i and i4=1
Although every cyclic group is an abelian group, not every abelian group is cyclic. The rational numbers under addition are abelian, not cyclic.
Abelian group
Consider the algebraic system (G, *), in which * represents a binary operation on G. The system (G, *) is therefore considered to be an abelian group if it satisfies all of the group's properties plus the following property:
(1) The operation * is commutative i.e.,
a * b = b * a ∀ a, b ∈G
Example - Consider the algebraic system (G, *), in which G represents the set of all non-zero real numbers and * represents a binary operation defined by
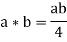
Demonstrate that the group (G, *) is an abelian one.
Solution:
Closure property - Because a * b 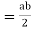 Subgroup is a real number, the set G is closed by the operation *. As a result, it belongs to G.
Subgroup is a real number, the set G is closed by the operation *. As a result, it belongs to G.
Associative property - * is an associative operation. If we use a, b, c∈G, we get
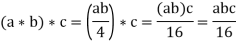
Similarly,
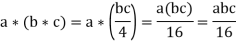
Identity - Assume that e is a +ve real number to get the identity element. Then e * a = a, with a being G.
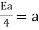 or
or 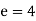
Similarly,

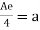 or
or 
As a result, G's identification element is 4.
Inverse - Let's pretend that a ∈G. If the inverse of an is a-1∈Q, then a * a-1=4.
Therefore  or
or 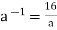
Similarly, 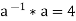
Therefore, 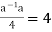 or
or 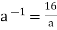
As a result, in G, the inverse of element an is  .
.
Commutative - * on G is a commutative operation.
Since 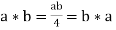
G, * is thus a closed, associative, identity element, inverse, and commutative algebraic system. As a result, the system (G, *) belongs to the abelian group.
Q5) Define cosets?
A5) Assume that H is a subgroup of G. For each x G, a left coset of H in G is a subset of G whose elements may be represented as xH= {xh | h ∈ H}. A representation of the coset is the element x. Similarly, for any x∈ G, a right coset of H in G is a subset that can be represented as Hx= {hx | h∈ H}. As a result, the complexes xH and Hx are referred to as a left coset and a right coset, respectively.
A left coset is denoted by x + H= {x+h | h ∈ H} if the group operation is additive (+), while a right coset is denoted by H + x = {h+x | h ∈ H} if the group operation is subtractive (-).
If G is a finite group, H is a subgroup of G, and g is an element of G, then in group theory;
The left coset of H in G with regard to the element of G is gH = gh: h an element of H.
And
The right coset of H in G with regard to the element of G is Hg = hg: h an element of H.
Let us now consider the lemmas that aid in the proof of the Lagrange theorem.
Lemma 1: If G is a group with a subgroup H, then H and any coset of H have a one-to-one relationship.
Lemma 2: If G is a group with subgroup H, then the left coset relation, g1∼g2, is an equivalence relation if and only if g1 ∗ H = g2 ∗ H.
Let S be a set and be an equivalence relation on S. Lemma 3: Let S be a set and be an equivalence relation on S. If A and B are two equivalence classes, then A ∩ B =∅,
A = B.
Q6) Explain Lagrange's theorem?
A6) One of the most important theorems in abstract algebra is the Lagrange theorem. It asserts that in group theory, the order of subgroup H of group G splits the order of G for any finite group G. The number of elements is represented by the group's order. Joseph-Louis Lagrange proved this theorem. Let us look at the statement and proof of the Lagrange theorem in Group theory, as well as the three lemmas that were utilized to prove this theorem with examples.
Lagrange Theorem Statement
The order of the subgroup H separates the order of the group G, according to the assertion. This can be written as:
|G| = |H|
The important terminologies and three lemmas that aid in the proof of the Lagrange theorem must be understood before proceeding with the proof.
Lagrange Theorem Proof
We may simply prove the Lagrange statement using the three lemmas presented before.
Proof of Lagrange Statement:
Let H be any subgroup of a finite group G of order m of order n. Take a look at G's cost breakdown in relation to H.
Let us now imagine that each coset of aH consists of n distinct items.
Let H = {h1,h2,…,hn}, then ah1,ah2,…,ahn are the n distinct members of aH.
Suppose, ahi=ahj⇒hi=hj be the cancellation law of G.
Because G is a finite group, there will be a finite number of discrete left cosets, say p. As a result, m=np since the total number of elements in all cosets equals np, which is equal to the total number of elements in G.
p = m/n
This proves that n, H's order, is a divisor of m, the finite group G's order. We can also observe that the index p is a divisor of the group's order.
Hence, proved, |G| = |H|
Q7) What is a normal subgroup?
A7) Let G stand for a group. If for any h ∈ H and x ∈ G, x h x-1∈ H, a subgroup H of G is said to be a normal subgroup of G.
If x H x-1 = {x h x-1| h ∈ H} then H is normal in G if and only if xH x-1⊆H, ∀ x∈ G.
Statement - Every subgroup H of G is normal in G if G is an abelian group.
Proof: Allow any h ∈ H, x ∈ G, and then
x h x-1= x (h x-1)
x h x-1= (x x-1) h
x h x-1 = e h
x h x-1 = h∈ H
As a result, H is a normal subgroup of G.
Q8) Describe Permutation and Symmetric groups?
A8) The set of all bijections from the set to itself with composition of functions as the group action is called a symmetric group on a set. The set of all permutations of the set's elements is known as the permutation group.
A "permutation group" is a group that acts (faithfully) on a set; this includes both symmetric groups (which are the groups of all permutations of the set) and subgroups of symmetric groups.
Although all groups can be realized as permutation groups (by acting on themselves), this type of action is rarely useful in studying the group; on the other hand, special types of actions (irreducible, faithful, transitive, doubly transitive, etc.) can provide a wealth of information about the group. Jordan, for example, established that A7, S6, S5, and the Mathieu group M12 are the only finite sharply five transitive groups.
(A "sharply five transitive group" is a group G acting on a set X with five or more components, such that there exists one and only one g ∈ G such that g. ai=bi for every ten elements a1,...,a5, b1,...,b5 ∈ X, with ai ≠ aj for i ≠ j and bi ≠ bj for i ≠ j.)
(In fact, Jordan showed that the only finite sharply 𝑘-transitive groups for 𝑘≥4 are 𝑆k, 𝑆k+1, 𝐴k+2, 𝑀11, and 𝑀12.
A permutation group is composed of a group G and a faithful action: G×X →X on a set X (faithful here implies that if gx=x for all x, then g=e). Cayley's Theorem states that any group G can be thought of as a permutation group if X is the underlying set of G and multiplication is performed. However, because the set on which G acts is enormous, this results in an embedding of G into a very large symmetric group. If the set you're acting on is "small"-ish, you'll usually get additional information.
Cayley's Theorem was developed because, in the past, people only examined permutation groups: collections of functions that acted on sets (the sets of roots of a polynomial, the points on the plane via symmetries, etc.). Cayley was attempting to abstract the concept of group; however, he pointed out that his more abstract definition included all of the things that people were already thinking about, and that it did not introduce any new ones in the sense that any abstract group could be considered a permutation group.
Q9) Write about Group Homomorphisms?
A9) A homomorphism is a mapping f: G →G' that has the properties f (xy) =f(x) f(y), ∀ x, y ∈ G. Despite the fact that the binary operations of the groups G and G' are different, the mapping f preserves the group operation. The homomorphism condition is the one described above.
Kernel of Homomorphism: - The set {x∈ G | f(x) =e'} is the Kernel of a homomorphism f from a group G to a group G' with identity e'.
Ker f stands for the kernel of f.
If f: G→G' is a homomorphism of G into G', then f's image set is the range of the map f, indicated by f (G). Thus
Im (f) = f (G) = {f(x)∈ G'| x ∈G}
G' is considered a homomorphic image of G if f (G) =G'
Isomorphism
Let's consider two algebraic systems, (G1, *) and (G2,0), where * and 0 are both binary operations. If there is an isomorphic mapping f: G1→G2, the systems (G1, *) and (G2,0) are said to be isomorphic.
When two algebraic systems are structurally comparable, one can be produced from the other by merely keeping the elements and operations the same.
Example, consider the two algebraic systems (A1, *) and (A2, ⊡) illustrated in fig. Determine the isomorphism of the two algebraic systems.
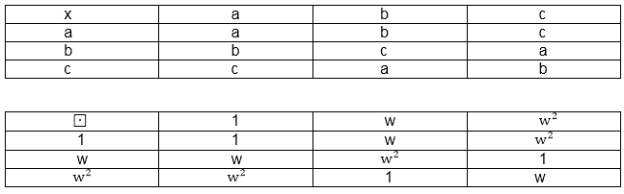
Solution - The two algebraic systems (A1, *) and (A2, ⊡), respectively, are isomorphic, and (A2, ⊡) is an isomorphic image of A1.
f (a)=1
f (b)=w
f (c)= w2
Automorphism
Let's consider two algebraic systems, (G1, *) and (G2,0), where * and 0 are binary operations on G1 and G2, respectively. If G1= G2, then an isomorphism from (G1, *) to (G2,0) is known as an automorphism.
Q10) Describe rings and its types?
A10) A ring is an algebraic system (R, +,) that satisfies the following conditions: R is a set with two arbitrary binary operations + and.
- (R, +) is an abelian group.
- (R, ∙) is a semigroup.
- The addition operation is distributive over the multiplication operation, i.e.,
a (b+c) =ab +ac and (b+c) a = ba + ca for all a, b, c ∈ R.
Example - Under the addition and multiplication modulo 9 operations, the set Z9 = 0, 1, 2, 3, 4, 5, 6, 7, 8 forms a ring.
Types of Rings
1. Commutative Rings:
A commutative ring (R, +,) is defined as one that holds the commutative law under multiplication, i.e., a. b = b. a, for any a, b ∈ R.
Example, Consider a set E of all even numbers that is subjected to addition and multiplication operations. A commutative ring is formed by the set E.
2. Ring with Unity:
If a ring (R, +,) has a multiplicative identity, it is called a ring with unity.
Example, Consider a set M of all 2 x 2 matrices over integers that are subjected to matrix multiplication and addition. With unity 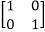 , the set M forms a ring.
, the set M forms a ring.
3. Ring with Zero Divisions:
If a.b=0, and a and b are any two non-zero R elements in the ring (R, +), then a and b are known as divisions of zero, and the ring (R, +) is known as ring with zero division.
4. Rings without Zero Division:
A ring without divisors of zero is an algebraic system (R, +) in which R is a set with two arbitrary binary operations + and we have a.b≠0 ⟹a≠0 and b ≠0 a for any a, b ∈ R.
Q11) If G = {1, -1, i, -i} where i=  , then show that G is an abelian group with respect to multiplication as a binary operation.
, then show that G is an abelian group with respect to multiplication as a binary operation.
A11) First we will construct a composition table-
. | 1 | -1 | i | -i |
1 | 1 | -1 | i | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | i | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties hold.
∴Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus, all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied
Hence (G, ⋅) is an abelian group.
Q12) Prove that every cyclic group is abelian.
A12) Suppose (G, *) be a cyclic group
Generated by a
x, y 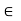 G
G
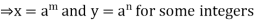
m and n
x * y = 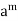 *
*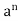
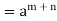
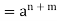
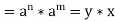
Q13) If (H, *) is a sub-group (G, *), then a * H = H if and only if a ∈H.
A13)
Let a * H = H
Since e ∈H then a = a * e ∈a * H
Hence a ∈H
Conversely
Let a ∈H then a * H ⊆H
(H, *) is a sub-group.
∴a∈H, h ∈H ⇒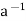 * h ∈H.
* h ∈H.
Now h ∈H
⇒h = a * (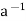 * h) ∈a * H
* h) ∈a * H
∴h∈H ⇒h ∈a * H
⇒H ⊆a * H
Hence a * H = H
Q14) If (R, +, .) is a ring with unity then for all a  R
R
(i) (-1) . a = - a
(ii) (-1) . (-1) = 1
A14)
(i) (-1) . a = - (1 . a) = - a
(ii) R is a ring with unity element, then 1 . a = a ∀ a 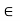 R
R
We have (1)a + (-1) . a = 1 . a + (-1) . a
= (1 + (-1)) . a
= 0 . a
= 0
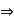 a + (–1) a = 0
a + (–1) a = 0
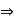 (-1) . a = - a
(-1) . a = - a
If a = –1, then (-1) . (-1) = - (-1)
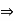 (-1) . (-1) = 1
(-1) . (-1) = 1