Unit - 3

Lattices

Q1) What are lattices?

A1) A lattice L can be defined in two ways. One method is to express L as a partially ordered set. For any pair of elements a, b L, a lattice L can be defined as a partially ordered set in which inf (a, b) and sup (a, b) exist. Another option is to axiomatically define a lattice L.

Let L be a non-empty set that can be closed using the binary operations meet and join, which are denoted by ∧ and ∨. If the following axioms hold, and a, b, and c are elements in L, then L is termed a lattice:

1) Commutative Law: -

(a) a ∧ b = b ∧ a           (b) a ∨ b = b ∨ a

2) Associative Law: -

(a) (a ∧ b) ∧ c = a ∧ (b∧ c)           (b) (a ∨ b) ∨ c = a ∨ (b ∨ c)

3) Absorption Law: -

(a) a ∧ (a ∨ b) = a          (b) a ∨ (a ∧ b) = a

Duality

Any statement in a lattice (L, ∧, ∨) has a dual, which is defined as a statement derived by interchanging ∧ an ∨.

Example: The dual of a ∧ (b ∨ a) = a ∨ a is a ∨ (b ∧ a) = a ∧ a

Q2) Write the properties of lattices?

A2) If a lattice L has a greatest element 1 and a least element 0, it is termed a bounded lattice.

Example

1. Because is the least element of P(S) and the set S is the greatest element of P, the power set P(S) of the set S under the operations of intersection and union is a bounded lattice ∅.
2. Because it has a least element 1 but no largest element, the set of +ve integer I+ in the normal order of ≤ is not a bounded lattice.

Properties of bounded lattice

If L is a bounded lattice, then we have the following identities for any element a ∈ L:

1. a ∨ 1 = 1
2. a ∧1= a
3. a ∨0=a
4. a ∧0=0

Theorem: Demonstrate that each finite lattice L = a1, a2, a3,...an is bounded.

Proof: We have given the finite lattice:

L = {a1,a2,a3....an}

Thus, the greatest element of Lattices L is a1∨ a2∨ a3∨....∨an.

Also, the least element of lattice L is a1∧ a2∧a3∧....∧an.

Since every finite lattice has the greatest and least elements. As a result, L is constrained.

Complemented lattice

Let L be a bounded lattice with lower and upper bounds of o and I, respectively. If L is true, let a be an element. If a ∨ x = I and a ∧ x = 0, an element x in L is considered a complement of a.

If a lattice L is bounded and every element in L has a complement, it is said to be complemented.

Determine the complement of a and c in the following example:

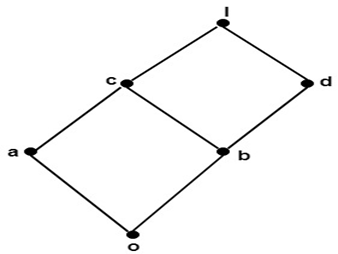
Fig: Example

Solution - The complement of the letter an is d. Because a ∨ d = 1 and a ∧ d = 0

There is no such thing as a complement of c. Since there is no element c with the properties c ∨ c'=1 and c ∧ c'=0,

Modular lattice

If a lattice satisfies the following property, it is called a modular lattice.

a^(b∨(a^d)) = (a^b) (a^d).

Fig: Example

Complete lattice

If all of a poset's subsets have both a join and a meet, it is called a complete lattice. Every full lattice, in particular, is a bounded lattice. Complete lattice homomorphisms are necessary to preserve arbitrary joins and meetings, whereas bounded lattice homomorphisms only retain finite joins and meets.

Every full semilattice poset is also a complete lattice. This finding is complicated by the fact that different definitions of homomorphism exist for this class of posets, depending on whether they are considered complete lattices, complete join-semilattices, complete meet-semilattices, or join-complete or meet-complete lattices.

It's worth noting that "partial lattice" isn't the polar opposite of "complete lattice"; rather, "partial lattice," "lattice," and "complete lattice" are all increasingly limited definitions.

Q3) What do you mean by boolean algebra?

A3) A Boolean Algebra is a supplemented distributive lattice. It is indicated as (B, ∧, ∨,',0,1), where B is a set that defines two binary operations ∧ (*) and ∨ (+) as well as a unary operation (complement). In this case, B has two unique elements: 0 and 1.

Each element of B has a unique complement since (B, ∧, ∨) is a complemented distributive lattice.

●      It deals with binary numbers & variables.

●      Therefore, also known as Binary Algebra or logical Algebra.

●      A mathematician named George Boole had developed this algebra in 1854.

●      The variables that are used in this algebra are known as Boolean variables.

●      Considering the range of voltages as logic ‘High’ is represented with ‘1’ and logic ‘Low’ is represented with ‘0’.

Postulates and Basic Laws of Boolean algebra

Here, the Boolean postulates and basic laws that are used are given underneath.

Boolean Postulates

●      Considering the binary numbers 0 and 1, Boolean variable (x) and its complement (x’).

●      They know as literal.

●      The possible logical OR operations are:

x + 0 = x

x + 1 = 1

x + x = x

x + x’ = 1

●      Similarly, the possible logical AND operations are:

x.1 = x

x.0 = 0

x.x = x

x.x’ = 0

●      These are the simple Boolean postulates and verification can be done by substituting the Boolean variable with ‘0’ or ‘1’.

Q4) Describe Axioms and Theorems of Boolean algebra?

A4) Basic Laws of Boolean algebra

●      The three basic laws of Boolean Algebra are:

●      Commutative law

●      Associative law

●      Distributive law

Commutative Law

●      The logical operation carried between two Boolean variables gives the same result irrespective of the order of the two variables, then that operation is said to be Commutative. The logical OR & logical AND operations between x & y are shown below

x + y = y + x

x.y=y.x

●      The symbol ‘+’ and ‘.’ indicates logical OR operation and logical AND operation.

●      Commutative law holds logical OR & logical AND operations.

Associative Law

●      If a logical OR operation of any two Boolean variables is performed first and then the same operation is performed with the remaining variable providing the same result, then that operation is said to be Associative. The logical OR & logical AND operations of x, y & z are:

x + (y + z) = (x + y) + z

x. (y.x) = (x.y).z

●      Associative law holds well for logical OR & logical AND operations.

Distributive Law

●      If a logical OR operation of any two Boolean variables is performed first and then AND operation is performed with the remaining variable, then that logical operation is said to be Distributive. The distribution of logical OR & logical AND operations between variables x, y & z are:

x. (y + z) = x.y + x.z

x + (y.x) = (x + y). (x + z)

●      Distributive law holds well for logical OR and logical AND operations.

●      These are the Basic laws of Boolean algebra and we can verify them by substituting the Boolean variables with ‘0’ or ‘1’.

Numerical

●      Simplify the Boolean function,

f = p’qr + pq’r + pqr’ + pqr

Method 1 -

Given f = p’qr + pq’r + pqr’ +pqr.

In first and second term r is common and in third and fourth terms pq is common.

So, taking out the common terms by using Distributive law we get,

⇒ f = (p’q + pq’) r + pq (r’ + r)

The terms present in first parenthesis can be simplified by using Ex-OR operation.

The terms present in second parenthesis is equal to ‘1’ using Boolean postulate we get

⇒ f = (p ⊕q) r + Pq (1)

The first term can’t be simplified further.

But, the second term is equal to pq using Boolean postulate.

⇒ f = (p ⊕q) r + pq

Therefore, the simplified Boolean function is f = (p⊕q) r + pq

Method 2

Given f = p’qr + pq’r + pqr’ + pqr.

Using the Boolean postulate, x + x = x.

Hence we can write the last term pqr two more times.

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Now using the Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms we get.

⇒ f = qr (p’ + p) + pr (q’ + q) + pq (r’ + r)

Using Boolean postulate, x + x’ = 1 and x.1 = x for further simplification.

⇒ f = qr (1) + pr (1) + pq (1)

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

Therefore, the simplified Boolean function is f = pq + qr + pr.

Hence, we got two different Boolean functions after simplification of the given Boolean function. Functionally, these two functions are same. As per requirement, we can choose one of them.

Numerical

Find the complement of the Boolean function,

f = p’q + pq’.

Solution:

Using Demerger’s theorem, (x + y)’ = x’.y’ we get

⇒ f’ = (p’q)’.(pq’)’

Then by second law, (x.y)’ = x’ + y’ we get

⇒ f’ = {(p’)’ + q’}. {p’ + (q’)’}

Then by using, (x’)’=x we get

⇒ f’ = {p + q’}. {p’ + q}

⇒ f’ = pp’ + pq + p’q’ + qq’

Using x.x’=0 we get

⇒ f = 0 + pq + p’q’ + 0

⇒ f = pq + p’q’

Therefore, the complement of Boolean function, p’q + pq’ is pq + p’q’.

Q5) What is Algebraic manipulation of Boolean expressions?

A5) Standard forms of Boolean expressions

●      Four product combinations are obtained by combining two variables x and y with logical AND operation. They are called as min terms or standard product terms. The min terms are given as x’y’, x’y, xy’ and xy.

●      In the same way, four Boolean sum terms are obtained by combining two variables x and y with logical OR operation. They are called as Max terms or standard sum terms. The Max terms are given as x + y, x + y’, x’ + y and x’ + y’.

The following table represents the min terms and MAX terms for 2 variables.

●      If the binary variable is ‘0’, then it is represented as complement of variable in min term and as the variable itself in Max term.

●      Similarly, if it is ‘1’, then it is represented as complement of variable in Max term and as the variable itself in min term.

●      From the above table, we can easily notice that min terms and Max terms are complement of each other.

●      If there are ‘n’ Boolean variables, then there will be 2n min terms and 2n Max terms.

Canonical SoP and PoS forms

●      A truth table comprises of a set of inputs and output(s).

●      If there are ‘n’ input variables, then there shall be 2n possible combinations comprising of zeros and ones.

●      So, the value of every output variable depends on the combination of input variables.

●      Hence, each output variable has ‘1’ for some combination and ‘0’ for other combination of input variables.

Q6) Explain canonical SoP form, with example?

A6) Canonical SoP form

●      It means Canonical Sum of Products form.

●      In this, each product term contains all literals.

●      So that these product terms are nothing but the min terms.

●      Hence is also known as sum of min terms form.

●      Firstly, identification of the min terms is done and then the logical OR of those min terms is taken in order to get the Boolean expression (function) corresponding to that output variable.

●      This Boolean function will be in sum of min terms form.

●      Then following the same procedure for other output variables too.

Example

Consider the following truth table.

●      Here, the output (f) is ‘1’ for only four combinations of inputs.

●      The corresponding min terms are given as p’qr, pq’r, pqr’, pqr.

●      By doing logical OR, we get the Boolean function of output (f).

●      Hence, the Boolean function of output is,

f = p’qr + pq’r + pqr’ + pqr.

●      This is the desired canonical SoP form of output, f.

●      It can also be represented as:

f=m3+m5+m6+m7f=m3+m5+m6+m7

f=∑m (3, 5, 6, 7) f=∑m (3, 5, 6, 7)

●      First, we represented the function as sum of respective min terms and then, the symbol for summation of those min terms is used.

Q7) Explain canonical PoS form?

A7) Canonical PoS form

●      It means Canonical Product of Sums form.

●      Here In this form, each sum term contains all literals.

●      These sum terms are the Max terms.

●      Hence, canonical PoS form is also known as product of Max terms form.

●      Identification of the Max terms for which the output variable is zero is done and then the logical AND of those Max terms is done in order to get the Boolean expression corresponding to that output variable.

●      This Boolean function is in the form of product of Max terms.

●      Following the same procedure for other output variables too.

Standard SoP and PoS forms

Standard SoP form

●      It stands for Standard Sum of Products form.

●      In this, each product term need not contain all literals.

●      So, the product terms can or cannot be the min terms.

●      Therefore, it is therefore the simplified form of canonical SoP form.

Standard SoP of output variable can be obtained by two steps.

●      Getting the canonical SoP form of output variable

●      Simplification the above Boolean function.

The same procedure is followed for other output variables too, if there is more than one output variable.

Numerical

Convert the Boolean function into Standard SoP form.

f = p’qr + pq’r + pqr’ + pqr

Solution:

Step 1 – By using the Boolean postulate, x + x = x and also writing the last term pqr two more times we get

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Step 2 – By Using Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms.

⇒ f = qr (p’ + p) + pr (q’ + q) + pq (r’ + r)

Step 3 – Then Using Boolean postulate, x + x’ = 1 we get

⇒ f = qr (1) + pr (1) + pq (1)

Step 4 – hence using Boolean postulate, x.1 = x we get

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

This is the required Boolean function.

Standard PoS form

●      It stands for Standard Product of Sum form.

●      Here, each sum term need not contain all literals.

●      So, the sum terms can or cannot be the Max terms.

●      Therefore, it is the desired simplified form of canonical PoS form.

Standard PoS form of output variable is obtained by two steps.

●      Getting the canonical PoS form of output variable

●      Simplification of the above Boolean function.

The same procedure is followed for other output variables too.

Numerical

Convert the Boolean function into Standard PoS form.

f = (p + q + r). (p + q + r’). (p + q’ + r). (p’ + q + r)

Solution:

Step 1 – By using the Boolean postulate, x.x = x and writing the first term p+q+r two more times we get

⇒ f = (p + q + r). (p + q + r). (p + q + r). (p + q + r’). (p +q’ + r). (p’ + q + r)

Step 2 – Now by using Distributive law, x + (y.x) = (x + y). (x + z) for 1st and 4th parenthesis, 2nd and 5th parenthesis, 3rd and 6th parenthesis.

⇒ f = (p + q + rr’). (p + r + qq’). (q + r + pp’)

Step 3 − Applying Boolean postulate, x.x’=0 for simplifying of the terms present in each parenthesis.

⇒ f = (p + q + 0). (p + r + 0). (q + r + 0)

Step 4 − Using Boolean postulate, x + 0 = x we get

⇒ f = (p + q). (p + r). (q + r)

⇒ f = (p + q). (q + r). (p + r)

This is the simplified Boolean function.

Hence, both Standard SoP and Standard PoS forms are Dual to one another.

Q8) How to simplify the boolean function?

A8) One Boolean statement is minimized into an equivalent expression using Boolean identities in this method.

Problem 1:

Minimize the following Boolean expression using Boolean identities −

F (A, B, C) =(A+B) (A+C)

Solution:

Given, F (A, B, C) =(A+B) (A+C)

Or, F (A, B, C) =A. A+A.C+B. A+B.C

[Applying distributive Rule]

Or, F (A, B, C) =A+A.C+B. A+B.C

[Applying Idempotent Law]

Or, F (A, B, C) =A(1+C) +B. A+B.C

[Applying distributive Law]

Or, F (A, B, C) =A+B.A+B.C

[Applying dominance Law]

Or, F (A, B, C) =(A+1). A+B.C

[Applying distributive Law]

Or, F (A, B, C) =1. A+B.C

[Applying dominance Law]

Or, F (A, B, C) =A+B.C

[Applying dominance Law]

So, F (A, B, C) =A+BC  is the minimized form.

Q9) Reduce the following Boolean expression to its simplest form using Boolean identities:

F (A, B, C) =A′B+BC′+BC+AB′C′

A9) Given, F (A, B, C) =A′B+BC′+BC+AB′C′

Or, F (A, B, C) =A′B+(BC′+BC′) +BC+AB′C′

[By idempotent law, BC’ = BC’ + BC’]

Or, F (A, B, C) =A′B+(BC′+BC) +(BC′+AB′C′)

Or, F (A, B, C) =A′B+B(C′+C) +C′(B+AB′)

[By distributive laws]

Or, F (A, B, C) =A′B+B.1+C′(B+A)

[ (C' + C) = 1 and absorption law (B + AB’) = (B + A)]

Or, F (A, B, C) =A′B+B+C′(B+A)

[ B.1 = B]

Or, F (A, B, C) =B(A′+1) +C′(B+A)

Or, F (A, B, C) =B.1+C′(B+A)

[ (A' + 1) = 1]

Or, F (A, B, C) =B+C′(B+A)

[ As, B.1 = B]

Or, F (A, B, C) =B+BC′+AC′

Or, F (A, B, C) =B(1+C′) +AC′

Or, F (A, B, C) =B.1+AC′

[As, (1 + C') = 1]

Or, F (A, B, C) =B+AC′

[As, B.1 = B]

So, F (A, B, C) =B+AC′ is the minimized form.

Q10) Describe Karnaugh map?

A10) Karnaugh map method or K-map method is the pictorial representation of the Boolean equations and Boolean manipulations are used to reduce the complexity in solving them. These can be considered as a special or extended version of the ‘Truth table’.

●      Karnaugh map can be explained as “An array containing 2k cells in a grid like format, where k is the number of variables in the Boolean expression that is to be reduced or optimized”. As it is evaluated from the truth table method, each cell in the K-map will represent a single row of the truth table and a cell is represented by a square.

●      The cells in the k-map are arranged in such a way that there are conjunctions, which differ in a single variable, are assigned in adjacent rows. The K-map method supports the elimination of potential race conditions and permits the rapid identification.

●      By using Karnaugh map technique, we can reduce the Boolean expression containing any number of variables, such as 2-variable Boolean expression, 3-variable Boolean expression, 4-variable Boolean expression and even 7-variable Boolean expressions, which are complex to solve by using regular Boolean theorems and laws.

Minimization with Karnaugh Maps and advantages of K-map:

●      K-maps are used to convert the truth table of a Boolean equation into minimized SOP form.

●      Easy and simple basic rules for the simplification.

●      The K-map method is faster and more efficient than other simplification techniques of Boolean algebra.

●      All rows in the K-map are represented by using square shaped cells, in which each square in that will represent a minterms.

●      It is easy to convert a truth table to k-map and k-map to Sum of Products form equation.

There are 2 forms in converting a Boolean equation into K-map:

Un-optimized form

Optimized form

●      Un-optimized form: It involves in converting the number of 1’s into equal number of product terms (min terms) in an SOP equation.

●      Optimized form: It involves in reducing the number of min terms in the SOP equation.

Q11) Define logic gates?

A11) The basic gates are namely AND gate, OR gate & NOT gate.

AND gate

It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.

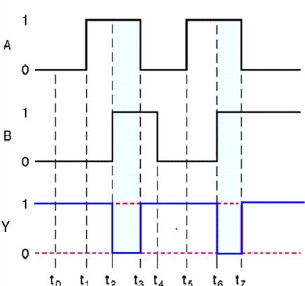
The following is the truth table of 2-input AND gate.

Here A, B are the inputs and Y is the output of two input AND gate.

If both inputs are ‘1’, then only the output, Y is ‘1’. For remaining combinations of inputs, the output, Y is ‘0’.

The figure below shows the symbol of an AND gate, which is having two inputs A, B and one output, Y.

Fig.: AND gate

Timing Diagram:

OR gate

It is a digital circuit which has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.

The truth table of 2-input OR gate is:

Here A, B are the inputs and Y is the output of two input OR gate.

When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.

The figure below shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

Fig: OR gate

Timing Diagram:

NOT gate

It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called as an inverter.

The truth table of NOT gate is:

Here A and Y are the corresponding input and output of NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.

The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.

Fig: NOT gate

Timing Diagram:

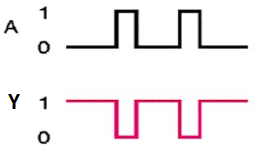
NAND gate

It is a digital circuit which has two or more inputs and single output and it is the inversion of logical AND gate.

The truth table of 2-input NAND gate is:

Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the inputs is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.

The image shows the symbol of NAND gate:

Fig: NAND gate

NAND gate works same as AND gate followed by an inverter.

Timing Diagram:

NOR gate

It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.

The truth table of 2-input NOR gate is:

Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If any one of the inputs is ‘1’, then the output is ‘0’. This is exactly opposite to two input OR gate operation.

The symbol of NOR gate is:

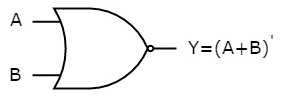
Fig: NOR gate

NOR gate works exactly same as that of OR gate followed by an inverter.

Timing Diagram:

Ex-OR gate

It stands for Exclusive-OR gate. Its function varies when the inputs have even number of ones.

The truth table of 2-input Ex-OR gate is:

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.

The symbol of Ex-OR gate is as follows:

Fig: XOR gate

It is similar to that of OR gate with an exception for few combination(s) of inputs. Hence, the output is also known as an odd function.

Timing Diagram:

Ex-NOR gate

It stands for Exclusive-NOR gate. Its function neither is same as that of NOR gate except when the inputs having even number of ones.

The truth table of 2-input Ex-NOR gate is:

Here A, B are the inputs and Y is the output. It is same as Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0, when both the inputs are one.

Hence the output of Ex-NOR gate is ‘1’, when both inputs are same and 0, when both the inputs are different.

The symbol of Ex-NOR gate is:

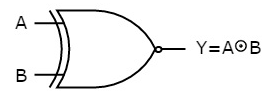
Fig: XNOR gate

It neither is similar to NOR gate except for few combinations of inputs. Here the output is ‘1’, when even number of 1 is present at the inputs. Hence is also called as an even function.

Timing Diagram:

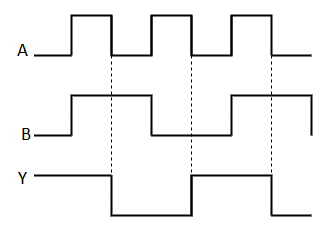
Q12) Define digital circuit and Boolean algebra?

A12) The truth tables for the OR, AND, and NOT gates are identical to the truth tables for the propositions p ∨ q (disjunction, "p or q"), p ∧ q (conjunction, "p and q"), and ¬p (negation, "not p"), respectively. The only change is that instead of T and F, 1 and 0 are utilized. As a result, logic circuits obey the same principles as propositions, forming a Boolean algebra. This is a formal statement of the result.

Theorem: Logic circuits form a Boolean Algebra

As a result, any Boolean algebra words, such as complements, literals, fundamental products, minterms, sum-of-products, and complete sum-of-products, can be employed with our logic circuits.

AND - OR circuits

An AND-OR circuit is a logic circuit that correlates to a Boolean sum-of-products statement.

(1) Some of the inputs or their complements are fed into each AND gate in a circuit L with multiple inputs.

(2) All of the AND gates' outputs are fed into a single OR gate.

(3) The circuit L's output is the output of the OR gate.

This type of logic circuit is seen in the diagram below.

An example AND-OR circuit with three inputs, A, B, C, and output Y is shown in Figure 15-12. In the inputs A, B, and C, we can easily express Y as a Boolean expression as follows. First, we need to figure out what each AND gate's output is.

(a) The first AND gate inputs are A, B, and C, hence the output is A. B. C.

(b) The second AND gate's inputs are A, B’, and C, hence the output is A. B’. C.

(c) The third AND gate's inputs are A’ and B; so, the output is A’. B.

The output of the OR gate, which is the circuit's output Y, is the total of the AND gates' outputs. Thus:

Y = A · B · C + A · B’· C + A’.  B

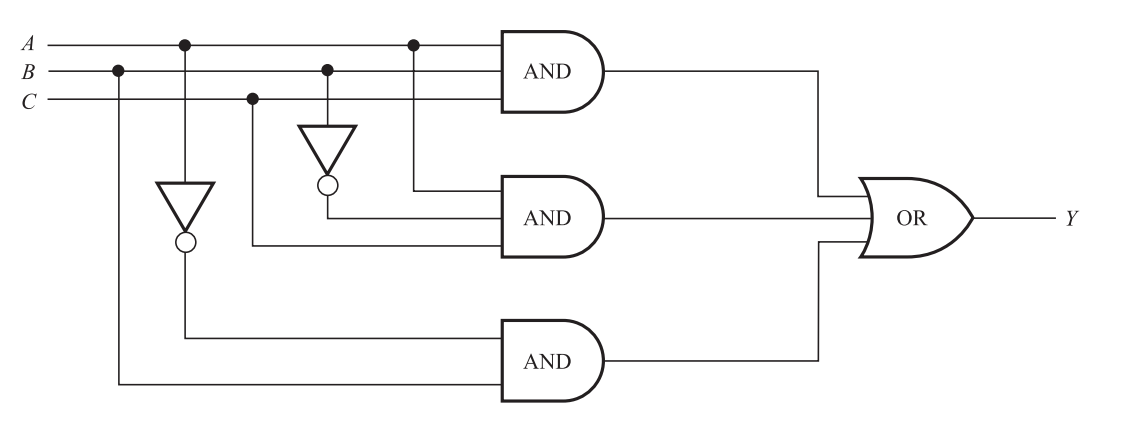
Fig: AND-OR circuit

NAND and NOR Gates

There are two more gates that are equal to combinations of the fundamental gates listed above.

(a) A NAND gate is the same as an AND gate followed by a NOT gate, as shown in Fig.(a).

(b) A NOR gate is the same as an OR gate followed by a NOT gate, as shown in Fig.(b).

Figure shows the truth tables for these gates (with two inputs A and B) (c). The NAND and NOR gates, like the corresponding AND and OR gates, can have two or more inputs. Furthermore, a NAND gate's output is 0 if and only if all of its inputs are 1, while a NOR gate's output is 1 if and only if all of its inputs are 0.

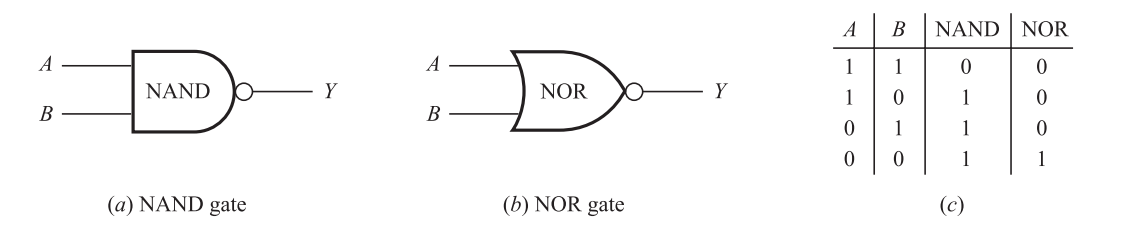
Fig: NAND and NOR Gates

The only difference between the AND and NAND gates and the OR and NOR gates is that the NAND and NOR gates both have a circle following them. A tiny circle is also used in some manuscripts to denote a complement before a gate. The Boolean expressions for two logic circuits in Fig., for example, are as follows:

(a) Y = (A’ B)’, (b) Y = (A’ + B’ + C)’ 

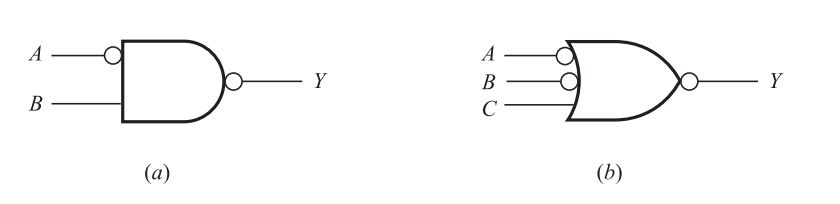
Fig: Two logic circuit

Q13) Minimize the following Boolean function-

F (A, B, C, D) = Σm (0, 1, 2, 5, 7, 8, 9, 10, 13, 15)

A13) Since the given Boolean expression has 4 variables, so we draw a 4 x 4 K Map.

We fill the cells of K Map in accordance with the given Boolean function.

Then, we form the groups in accordance with the above rules.

Then,

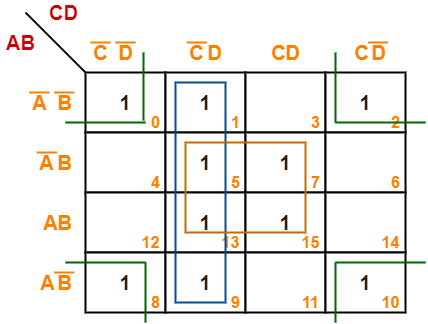
Now,

F (A, B, C, D)

= (A’B + AB) (C’D + CD) + (A’B’ + A’B + AB + AB’) C’D + (A’B’ + AB’) (C’D’ + CD’)

= BD + C’D + B’D’

Thus, minimized Boolean expression is-

F (A, B, C, D) = BD + C’D + B’D’

Q14) Minimize the following Boolean function-

F(A, B, C, D) = Σm(1, 3, 4, 6, 8, 9, 11, 13, 15) + Σd(0, 2, 14)

A14) Since the given Boolean expression has 4 variables, so we draw a 4 x 4 K Map.

We fill the cells of K Map in accordance with the given Boolean function.

Then, we form the groups in accordance with the above rules.

After that,

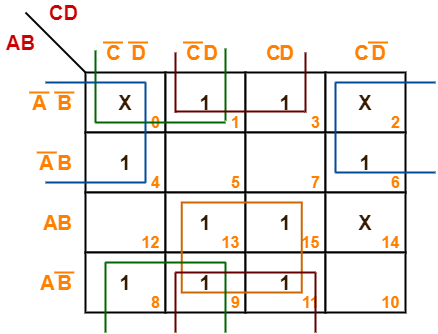
Now,

F (A, B, C, D)

= (AB + AB’) (C’D + CD) + (A’B’ + AB’) (C’D + CD) + (A’B’ + AB’) (C’D’ + C’D) + (A’B’ + A’B) (C’D’ + CD’)

= AD + B’D + B’C’ + A’D’

Thus, minimized Boolean expression is-

F (A, B, C, D) = AD + B’D + B’C’ + A’D’

Q15) Write the difference between SoP and PoS?

A15) Difference between SoP and PoS