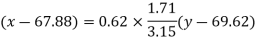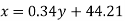Unit - 3

Statistical techniques-1

Q1) Find the arithmetic mean of the following dataset.

A1)

Let the assumed mean (a) = 25,

Q2) Find the mode of the following dataset-

A2)

Here the highest frequency is 9. So that the modal class is 40-50,

Put the values in the given data-

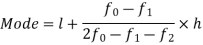
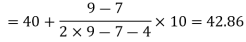
Hence the mode is 42.86

Q3) Define skewness and kurtosis.

A3) Skewness-

The word skewness means lack of symmetry-

The examples of the symmetric curve, positively skewed, and negatively skewed curves are given as follows-

1. Symmetric curve-

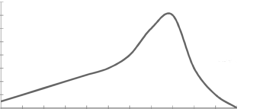
2. Positively skewed-

3. Negatively skewed-

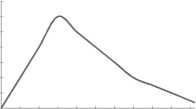
To measure the skewness we use Karl Pearson’s coefficient of skewness.

Then the formula is as follows-

Note- the value of Karl Pearson’s coefficient of skewness lies between -1 to +1.

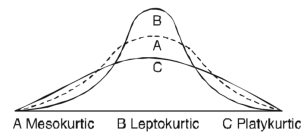
Kurtosis-

It is the measurement of the degree of peakedness of a distribution

Kurtosis is measured as-

Calculation of kurtosis-

The second and fourth central moments are used to measure kurtosis.

We use Karl Pearson’s formula to calculate kurtosis-

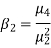
Now, three conditions arise-

1. If 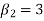, then the curve is mesokurtic.

2. If 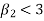, then the curve is platykurtic

3. If 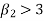 , then the curve is said to be leptokurtic.

Q4) Calculate Karl Pearson’s coefficient of skewness of marks obtained by 150 students.

A4)

Mode is not well defined so that first we calculate mean and median-

Class	f	x	CF		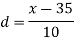Fd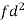
0-10	10	5	10	-3	-30	90
10-20	40	15	50	-2	-80	160
20-30	20	25	70	-1	-20	20
30-40	0	35	70	0	0	0
40-50	10	45	80	1	10	10
50-60	40	55	120	2	80	160
60-70	16	65	136	3	48	144
70-80	14	75	150	4	56	244

Now,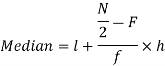
 

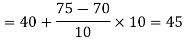
And

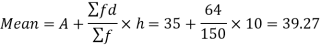
Standard deviation-

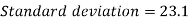
Then-

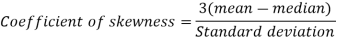
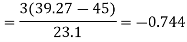
Q5) Calculate the median, quartiles, and the quartile coefficient of skewness from the following data:

A5) Here total frequency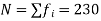

The cumulative frequency table is

Now, N/2 =230/2= 115th item which lies in the 110 – 120 group.

Median or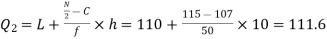

Also, 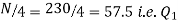is 57.5th or 58th item which lies in the 90-100 group.

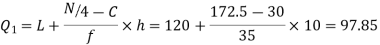
Similarly 3N/4 = 172.5 i.e. 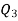is 173rd item which lies in the 120-130 group.

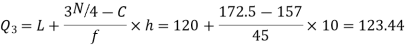
Hence quartile coefficient of skewness =

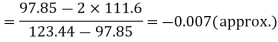
Q6) Find the best values of a and b so that y = a + bx fits the data given in the table

A6)

y = a + bx

x	y	Xy
0	1.0	0	0
1	2.9	2.0	1
2	4.8	9.6	4
3	6.7	20.1	9
4	8.6	13.4	16
x = 10	y ,= 24.0	xy = 67.0

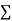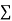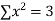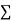Normal equations, y= na+ bx  (2)

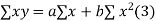
On putting the values of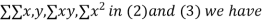

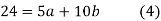
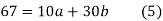
On solving (4) and (5) we get,

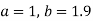
On substituting the values of a and b in (1) we get

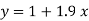
Q7) Find the straight line that best fits the following data by using the method of least square.

A7)

Suppose the straight line

y = a + bx…….. (1)

Fits the best-

Then-

x	y	Xy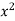
1	14	14	1
2	27	54	4
3	40	120	9
4	55	220	16
5	68	340	25
Sum = 15	204	748	55

Normal equations are-

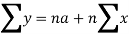
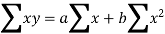
Put the values from the table, we get two normal equations-

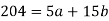
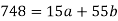
On solving the above equations, we get-

So that the best fit line will be- (on putting the values of a and b in equation (1))

Q8) Fit the curve 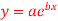by using the method of least square.

A8)

Here-

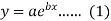
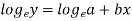
Now put-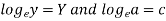

Then we get-

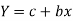
x	Y		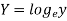XY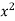
1	7.209	1.97533	1.97533	1
2	5.265	1.66108	3.32216	4
3	3.846	1.34703	4.04109	9
4	2.809	1.03283	4.13132	16
5	2.052	0.71881	3.59405	25
6	1.499	0.40480	2.4288	36
Sum = 21		7.13988	19.49275	91

Normal equations are-

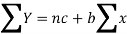
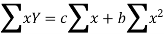
Putting the values form the table, we get-

7.13988 = 6c + 21b

19.49275 = 21c + 91b

On solving, we get-

b = -0.3141 and c = 2.28933

c =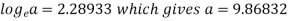

Now put these values in equations (1), we get-

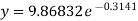
Q9) Find the correlation coefficient between the values X and Y of the dataset given below by using the short-cut method-

A9)

X	Y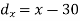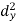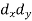
10	90	-20	400	20	400	-400
20	85	-10	100	15	225	-150
30	80	0	0	10	100	0
40	60	10	100	-10	100	-100
50	45	20	400	-25	625	-500
Sum = 150	360	0	1000	10	1450	-1150

Short-cut method to calculate correlation coefficient-

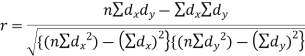
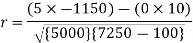
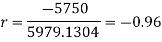
Q10) The correlation table given below shows that the ages of husband and wife of 53 married couples living together on the census night of 1991. Calculate the coefficient of correlation between the age of the husband and that of the wife.

A10)

Age of husband				Age of wife x series							Suppose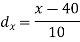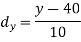
				15-25	25-35	35-45	45-55	55-65	65-75	Total    f
Years			Midpoint      x	20	30	40	50	60	70
Age group	Midpoint    y			-20	-10	0	10	20	30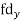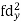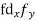
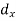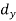				-2	-1	0	1	2	3
15-25	20	-20	-2	4 1	2 1					2	-4	8	6
25-35	30	-10	-1	4 2	12 12	0 1				15	-15	15	16
35-45	40	0	0		0 4	0 10	0 1			15	0	0	0
45-55	50					0 3	6 6	2 1		10	10	10	8
55-65	60						4 2	16 4	12 2	8	16	32	32
65-75	70							6 1	18 2	3	9	27	24
Total   f				3	17	14	9	6	4	53 = n	16	92	86
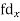				-6	-17	0	9	12	12	10	Thick figures in small sqs. For Check: 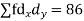From both sides
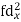				12	17	0	9	24	36	98
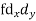				8	14	0	10	24	30	86

With the help of the above correlation table, we have

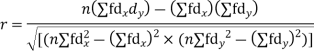
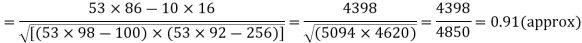
Q11) Three judges A,B,C give the following ranks. Find which pair of judges has common approach

A11) Here n = 10

A (=x)	Ranks by B(=y)	C (=z)	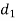x-y	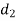y - z	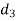z-x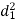
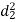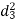1	3	6	-2	-3	5	4	9	25
6	5	4	1	1	-2	1	1	4
5	8	9	-3	-1	4	9	1	16
10	4	8	6	-4	-2	36	16	4
3	7	1	-4	6	-2	16	36	4
2	10	2	-8	8	0	64	64	0
4	2	3	2	-1	-1	4	1	1
9	1	10	8	-9	1	64	81	1
7	6	5	1	1	-2	1	1	4
8	9	7	-1	2	-1	1	4	1
Total			0	0	0	200	214	60

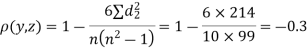
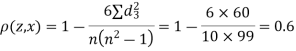
Since 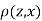is maximum, the pair of judge A and C have the nearest common approach.

Q12) Two variables X and Y are given in the dataset below, find the two lines of regression.

A12)

The two lines of regression can be expressed as-

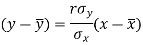
And

x	y		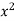	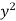Xy
65	66	4225	4356	4290
66	68	4356	4624	4488
67	65	4489	4225	4355
67	69	4489	4761	4623
68	74	4624	5476	5032
69	73	4761	5329	5037
70	72	4900	5184	5040
71	70	5041	4900	4970
Sum = 543	557	36885	38855	37835

Now-

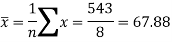
And

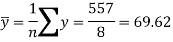
The standard deviation of x-

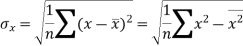
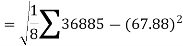
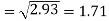
Similarly-

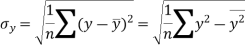
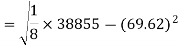
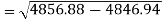
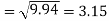
Correlation coefficient-

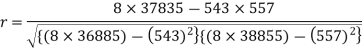
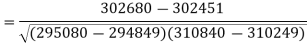
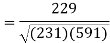
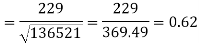
Put these values in the regression line equation, we get

Regression line y on x-

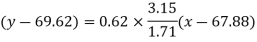
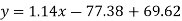
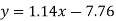
Regression line x on y-