Unit - 5
Statistical techniques-3
Q1) Define the population and sample.
A1)
Population-
The population is the collection or group of observations under study.
The total number of observations in a population is known as population size, and it is denoted by N.
Types of the population-
- Finite population – the population contains finite numbers of observations is known as finite population
- Infinite population- it contains an infinite number of observations.
- Real population- the population which comprises the items which are all present physically is known as the real population.
- Hypothetical population- if the population consists of the items which are not physically present but their existence can be imagined, is known as a hypothetical population.
Sample –
To extract the information from all the elements or units or items of a large population may be, in general, time-consuming, expensive, and difficult., and also if the elements or units of the population are destroyed under investigation then gathering the information from all the units is not make a sense. For example, to test the blood, doctors take a very small amount of blood. Or to test the quality of a certain sweet we take a small piece of sweet. In such situations, a small part of the population is selected from the population which is called a sample
Complete survey-
When each, and every element or unit of the population is investigated or studied for the characteristics under study then we call it a complete survey or census.
Sample Survey
When only a part of a small number of elements or units (i.e. sample) of the population are investigated or studied for the characteristics under study then we call it sample survey or sample enumeration Simple Random Sampling or Random Sampling
The simplest and most common method of sampling is simple random sampling. In simple random sampling, the sample is drawn in such a way that each element or unit of the population has an equal, and independent chance of being included in the sample. If a sample is drawn by this method then it is known as a simple random sample or random sample
Q2) Define the null and alternative hypothesis.
A2)
Simple and composite hypotheses-
If a hypothesis specifies only one value or exact value of the population parameter then it is known as a simple hypothesis., and if a hypothesis specifies not just one value but a range of values that the population parameter may assume is called a composite hypothesis.
The null and alternative hypothesis
The hypothesis is to be tested as called the null hypothesis.
The hypothesis which complements the null hypothesis is called the alternative hypothesis.
In the example of a car, the claim is 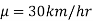 , and its complement is
, and its complement is 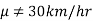 .
.
The null and alternative hypothesis can be formulated as-
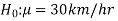
And
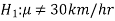
Q3) Define two types of error.
A3)
Type-1 and Type-2 error-
Type-1 error-
The decision relating to the rejection of null hypo. When it is true is called a type-1 error.
The probability of type-1 error is called the size of the test, it is denoted by 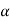 , and defined as-
, and defined as-
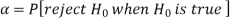
Note-
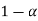 is the probability of a correct decision.
is the probability of a correct decision.
Type-2 error-
The decision relating to the non-rejection of null hypo. When it is false is called a type-1 error.
It is denoted by 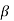 and defined as-
and defined as-
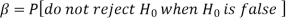
Decision |
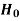 | 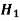 |
Reject 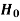 | Type-1 error | Correct decision |
Do not reject 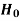 | Correct decision | Type-2 error |
Q4) How do we test the hypothesis for the population mean by using Z-test.
A4)
For testing the null hypothesis, the test statistic Z is given as-
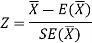
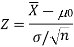
The sampling distribution of the test statistics depends upon variance 
So that there are two cases-
Case-1: when 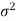 is known -
is known -
The test statistic follows the normal distribution with mean 0, and variance unity when the sample size is large as the population under study is normal or non-normal. If the sample size is small then test statistic Z follows the normal distribution only when the population under study is normal. Thus,
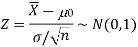
Case-2: when 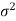 is unknown –
is unknown –
We estimate the value of 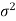 by using the value of sample variance
by using the value of sample variance
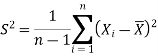
Then the test statistic becomes-
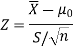
After that, we calculate the value of the test statistic as may be the case (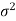 is known or unknown), and compare it with the critical value at the prefixed level of significance α.
is known or unknown), and compare it with the critical value at the prefixed level of significance α.
Q5) A manufacturer of ballpoint pens claims that a certain pen manufactured by him has a mean writing-life of at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with a standard deviation of 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at a 1% level of significance?
A5)
It is given that-
The specified value of the population mean = 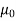 = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25
The null and alternative hypothesis will be-
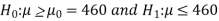
Also, the alternative hypothesis left-tailed so that the test is left tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should use a t-test for if the writing-life of the pen follows a normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by
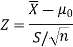
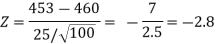
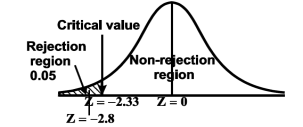
We get the critical value of left tailed Z test at 1% level of significance is 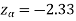
Since the calculated value of test statistic Z (= ‒2.8,) is less than the critical value
(= −2.33), that means the calculated value of test statistic Z lies in the rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at a 1% level of significance.
Q6) A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has an average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with a standard deviation of 90 hours. Should the company accept the new brand at a 5% level of significance?
A6)
Here we have-
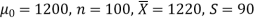
The company may accept the new CFL light when the average life of
CFL light is greater than 1200 hours. So the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So our claim is 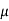 > 1200 and its complement is
> 1200 and its complement is 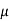 ≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
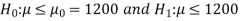
Since the alternative hypothesis is right-tailed so the test is right-tailed.
Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use a t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for a Z-test instead of a t-test.
Therefore, the test statistic is given by
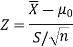
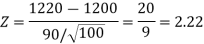
The critical values for a right-tailed test at a 5% level of significance is
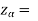 1.645
1.645
Since the calculated value of test statistic Z (= 2.22) is greater than the critical value (= 1.645), that means it lies in the rejection region so we reject the null hypothesis and support the alternative hypothesis i.e. we support our claim at a 5% level of significance
Thus, we conclude that the sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs
Q7) Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted from extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
A7)
We compute the mean and the S.D. Of the difference between the marks of the two tests as under:

Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.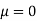
Then,  nearly and df v=11-1=10
nearly and df v=11-1=10
Students | 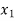 | 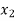 | 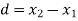 | 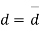 | 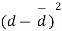 |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
| 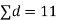 |
| 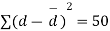 |
From Table IV, we find that 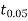 (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of 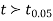 , the value of t is not significant at a 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at a 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
Q8) From a random sample of 10 pigs fed on diet A, the increase in weight in certain period were 10,6,16,17,13,12,8,14,15,9 lbs. For another random sample of 12 pigs fed on diet B, the increase in the same period were 7,13,22,15,12,14,18,8,21,23,10,17 lbs. Test whether diets A and B differ significantly as regards their effect on weight increases?
A8)
We calculate the means and standard derivations of the samples as follows
| Diet A |
|
| Diet B |
|
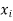 | 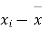 | 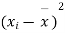 | 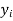 | 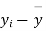 | 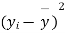 |
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 13 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 17 | 2 | 4 |
|
|
|
|
|
|
120 |
|
| 180 | 0 | 314 |
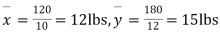
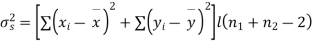
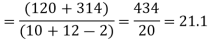
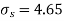
Assuming that the samples do not differ in weight so far as the two diets are concerned i.e. 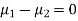
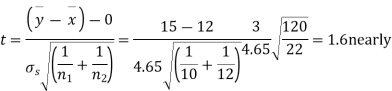
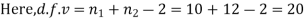
For v=20, we find 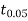 =2.09
=2.09
The calculated value of 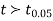
Hence the difference between the sample's means is not significant i.e. the two diets do not differ significantly as regards their effects on the increase in weight.
Q9) A college conducts both face-to-face and distance mode classes for a particular course intended both to be identical. A sample of 50 students of face to face mode yields examination results mean and SD respectively as-

And other samples of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:

Are both educational methods statistically equal at the 5% level?
A9)
Here we have-
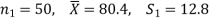
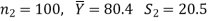
Here we wish to test that both educational methods are statistically equal. If 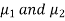 denote the average marks of face to face and distance mode students respectively then our claim is
denote the average marks of face to face and distance mode students respectively then our claim is 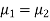 and its complement is
and its complement is 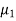 ≠
≠  . Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,

Since the alternative hypothesis is two-tailed so the test is two-tailed.
We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So we should go for a t-test if the population of difference is known to be normal. But it is not the case.
Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.
For testing the null hypothesis, the test statistic Z is given by
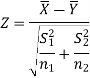
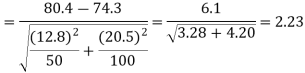
The critical (tabulated) values for a two-tailed test at a 5% level of significance are-
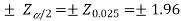
Since the calculated value of Z (= 2.23) is greater than the critical values
(= ±1.96), that means it lies in the rejection region so we
Reject the null hypothesis i.e. we reject the claim at a 5% level of significance
Q10) A tyre manufacturer claims that the average life of a particular category of his tyre is 18000 km when used under normal driving conditions. A random sample of 16 tyres was tested. The mean and SD of life of the tyres in the sample were 20000 km and 6000 km respectively.
Assuming that the life of the tyres is normally distributed, test the claim of the manufacturer at a 1% level of significance using the appropriate test.
A10)
Here we have-
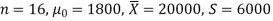
We want to test that manufacturer’s claim is true that the average
Life ( ) of tyres is 18000 km. So claim is μ = 18000 and its complement
) of tyres is 18000 km. So claim is μ = 18000 and its complement
Is μ ≠ 18000. Since the claim contains the equality sign so we can take
The claim as the null hypothesis and complement as the alternative
Hypothesis. Thus,
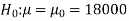
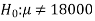
Here, population SD is unknown and the population under study is given to
Be normal.
So here can use t-test-
For testing the null hypothesis, the test statistic t is given by-

The critical value of test statistic t for two-tailed test corresponding (n-1) = 15 df at 1% level of significance are 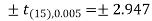
Since the calculated value of test statistic t (= 1.33) is less than the critical (tabulated) value (= 2.947) and greater than that critical value (= − 2.947), that means the calculated value of test statistic lies in the non-rejection region, so we do not reject the null hypothesis. We conclude that the sample fails to provide sufficient evidence against the claim so we may assume that manufacturer’s claim is true.
Q11) Two sources of raw materials are under consideration by a bulb manufacturing company. Both sources seem to have similar characteristics but the company is not sure about their respective uniformity. A sample of 12 lots from source A yields a variance of 125 and a sample of 10 lots from source B yields a variance of 112. Is it likely that the variance of source A significantly differs from the variance of source B at significance level α = 0.01?
A11)
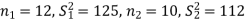
The null and alternative hypothesis will be-
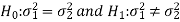
Since the alternative hypothesis is two-tailed so the test is two-tailed.
Here, we want to test the hypothesis about two population variances and sample sizes  = 12(< 30) and
= 12(< 30) and 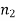 = 10 (< 30) are small. Also, populations under study are normal and both samples are independent.
= 10 (< 30) are small. Also, populations under study are normal and both samples are independent.
So we can go for F-test for two population variances.
The test statistic is-

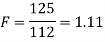
The critical (tabulated) value of test statistic F for the two-tailed test corresponding 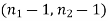 = (11, 9) df at 5% level of significance are
= (11, 9) df at 5% level of significance are  and
and
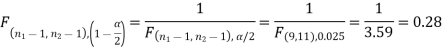
Since the calculated value of test statistic (= 1.11) is less than the critical value (= 3.91) and greater than the critical value (= 0.28), that means the calculated value of test statistic lies in the non-rejection region, so we do not reject the null hypothesis and reject the alternative hypothesis. We conclude that samples provide us sufficient evidence against the claim so we may assume that the variances of source A and B differ.
Q12) A set of five similar coins is tossed 320 times and the result is
Number of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
A12)
For v = 5, we have 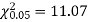
P, probability of getting a head=1/2; q, probability of getting a tail=1/2.
Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion 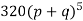


Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.
Hence, 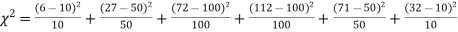

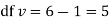
Since the calculated value of 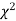 is much greater than
is much greater than 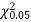 the hypothesis that the data follow the binomial law is rejected.
the hypothesis that the data follow the binomial law is rejected.
Q13) In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
A13)
The corresponding frequencies are
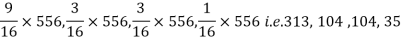
Hence,
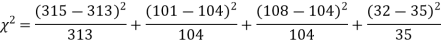
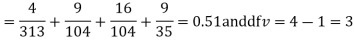
For v = 3, we have 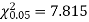
Since the calculated value of 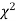 is much less than
is much less than 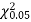 there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
For v = 3, we have 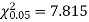
Since the calculated value of 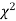 is much less than
is much less than 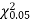 there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
Q14) An investigator is interested to know the quality of certain electronic products in four different shops.
He takes 5, 6, 7, 6 products and gives them a score out of 10 as given in the table-
Shop-1 | 8 6 7 5 9 |
Shop-2 | 6 4 6 5 6 7 |
Shop-3 | 6 5 5 6 7 8 5 |
Shop-4 | 5 6 6 7 6 7 |
A14)
If 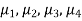 denote the average score of electronic products of 4 shops then-
denote the average score of electronic products of 4 shops then-
Null hypothesis-

Alternative hypothesis-

S. No. | 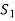 |  | 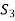 | 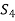 | 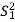 | 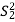 | 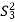 | 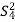 |
1 | 8 | 6 | 6 | 5 | 64 | 36 | 36 | 25 |
2 | 6 | 4 | 5 | 6 | 36 | 16 | 25 | 36 |
3 | 7 | 6 | 5 | 6 | 49 | 36 | 25 | 36 |
4 | 5 | 5 | 6 | 7 | 25 | 25 | 36 | 49 |
5 | 9 | 6 | 7 | 6 | 81 | 36 | 49 | 36 |
6 |
| 7 | 8 | 7 |
| 49 | 64 | 49 |
7 |
|
| 5 |
|
|
| 25 |
|
Total | 35 | 34 | 42 | 37 | 255 | 198 | 260 | 231 |
Total = 148
Correction factor = 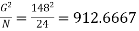
The raw sum of squares (RSS) =

Total sum of squares (TSS) = RSS – CF = 944 – 912.6667 = 31.3333
Sum of squares due to treatment (SST)-
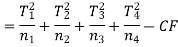
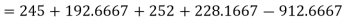
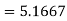
Sum of squares due to error (SSE) = TSS – SST = 31.3333 – 5.1667 = 26.1666
Now-

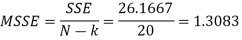
ANOVA TABLE
Sources of variation | Df | SS | MSS | F |
Between shops | 3 | 5.1667 | 1.7222 | F = 1.7222 / 1.3083 = 1.3164 |
Within shops | 20 | 26.1666 | 1.3083 |
|
Here calculated F = 1.3164
Tabulated F at 5% level of significance with (3, 20) degree of freedom is 3.10.
Conclusion: Since Calculated F < Tabulated F, so we may accept H0 and conclude that the quality of shops does not differ significantly.
Q15) The following figures relate to production in kg. Of three varieties P, Q, R of wheat shown in 12 plots
P 14 16 18
Q 14 13 15 22
R 18 16 19 15 20
Is there any significant difference in the production of these varieties?
A15)
The null hypothesis is-
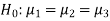
And the alternative hypothesis is-
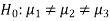
Grand total = 14+16+18+14+13+15+22+18+16+19+19+20 = 204
N = Total number of observations = 12
Correction factor-
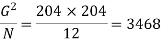
The raw sum of squares (RSS) =
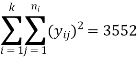
Total sum of squares (TSS) = RSS – CF = 3552 – 3468 = 84
Sum of squares due to treatment (SST)-
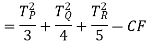
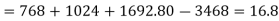
Sum of squares due to error (SSE) = TSS – SST = 84 – 16.8 = 67.2
Now-
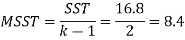

So that-
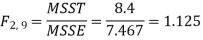
Sources of variation | Df | SS | MSS | F |
Between varities | 2 | 16.8 | 8.4 | F = 8.4/7.46 = 1.12 |
Due to error | 12 | 67.20 | 7.467 |
|
Total | 14 | 84 |
|
|
For 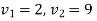 the tabulated value of F at 5% level significance is 4.261. Since the calculated value F is less than the table value of F, we accept the null hypotheses and conclude that there is no significant difference in their mean productivity of three varieties P, Q, and R.
the tabulated value of F at 5% level significance is 4.261. Since the calculated value F is less than the table value of F, we accept the null hypotheses and conclude that there is no significant difference in their mean productivity of three varieties P, Q, and R.