Unit -1

Basic Concepts and Automata Theory

Q .1) Difference between DFA and NFA?

Sol:

Q.2) what is the application of Finite Automata ?

Sol : Application of Finite Automata is :

1. Finite Automata (FA) –

●      Used in text editors.

●      For the implementation of spell checkers.

2. Push Down Automata (PDA) –

●      For designing the parsing phase of a compiler (Syntax Analysis).

●      For evaluating the arithmetic expressions.

3. Linear Bounded Automata (LBA) –

●      For implementation of genetic programming.

●      For constructing syntactic parse trees for semantic analysis of the compiler.

4. Turing Machine (TM) –

●      For implementation of neural networks and Robotics Applications.

●      For implementation of artificial intelligence.

Q.3)  How to convert NFA to DFA ?

Sol : In NFA, the device goes to multiple states when a particular input is given to the current state. On a given input symbol, it can have zero, one or more than a move. On the other hand, in DFA, the program goes to only one state when a particular input is given to the current state. On a given input symbol, a DFA has only one move.

Let, M = (Q, ∑, δ, q0, F) is an NFA which accepts the language L(M). There should be equivalent DFA denoted by M' = (Q', ∑', q0', δ', F') such that L(M) = L(M')

Steps for Converting NFA to DFA -

Step 1: Initially Q' = ϕ

Step 2: Add q0 of NFA to Q'. Then find the transitions from this start state.

Step 3: In Q', find the possible set of states for each input symbol. If this set of states is not in Q', then add it to Q'.

Step 4: In DFA, the final state will be all the states which contain F(final states of NFA)

Q.4) Write the steps for converting from Mealy Machine to Moore Machine ?

Sol: The output is connected with each state in the Moore machine and the output is given across the edge with an input symbol in the Mealy machine. State output symbols are distributed to the input symbol paths to convert the Moore machine to the Mealy machine. But we will create a separate state for and new output symbol when converting the Mealy machine to Moore machine and are distributed according to incoming and outgoing edges.

The following steps are used for converting Mealy machine to the Moore machine:

Step 1: For each state(Qi), calculate the number of different outputs that are available in the transition table of the Mealy machine.

Step 2: Copy state Qi, if all the outputs of Qi are the same. Break qi into n states as Qin, if it has n distinct outputs where n = 0, 1, 2....

Step 3: If the output of initial state is 0, insert a new initial state at the starting which gives 1 output.

Q.5) For the given set make Transition Diagram and Transition Table for DFA ?

1.     Q = {q0, q1, q2} 

2.     ∑ = {0,1} 

3.     q0 = {q0} 

4.     F = {q2} 

Sol :  Transition Diagram :

Transition Table :

Q.6) Convert the given Moore machine into its equivalent Mealy machine?

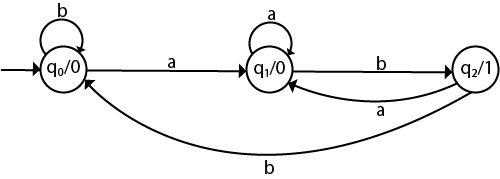
Sol : The transition table of given Moore machine is as follows:

The equivalent Mealy machine can be obtained as follows:

λ' (q0, a) = λ(δ(q0, a)) 

                = λ(q1) 

                = 0 

λ' (q0, b) = λ(δ(q0, b)) 

                = λ(q0) 

                = 0

The λ for state q1 is as follows:

λ' (q1, a) = λ(δ(q1, a)) 

                = λ(q1) 

                = 0 

λ' (q1, b) = λ(δ(q1, b)) 

                = λ(q2) 

                = 1 

The λ for state q2 is as follows:

λ' (q2, a) = λ(δ(q2, a)) 

                = λ(q1) 

                = 0 

λ' (q2, b) = λ(δ(q2, b)) 

                = λ(q0) 

                = 0 

Hence the transition table for the Mealy machine can be drawn as follows:

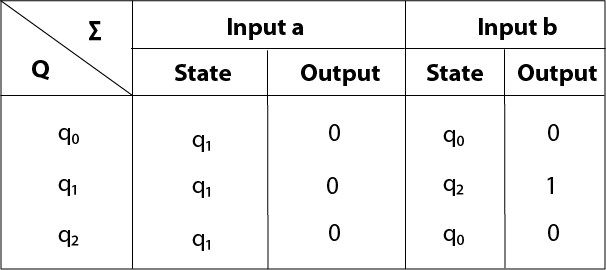
The equivalent Mealy machine will be

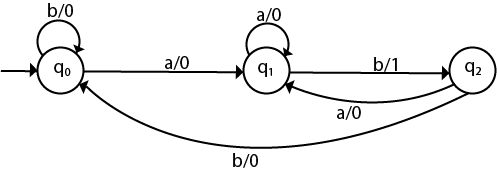
Q.7) What are the advantages and disadvantages of Deterministic Finite Automata (DFA)?

Sol: There are some advantages and disadvantages of DFA,

❖      The union/intersection of the languages recognized by two given DFAs.

❖      The complement of the language recognized by a given DFA.

❖      DFAs were invented to model of a Turing machine, which was too general to study properties of real world machines.

❖      DFAs are one of the most practical models of computation, since there is a trivial linear time, constant-space, online algorithm there are efficient algorithms to find a DFA recognizing.

❖      The classical example of a simply described language that no DFA can recognize is bracket language, i.e language that consists of properly paired brackets such as word "(( )( ))".

❖      On the other hand, finite state automata are of strictly limited power in the

Languages they can recognize; many simple languages, including any

Problem that requires more than constant space to solve, cannot be

Recognized by a DFA.

Q.8) Define Finite Automata in detail  and also define their types ?

Sol:finite automata is :

A finite automaton is a collection of 5-tuple (Q, ∑, δ, q0, F), where:

Finite Automata model are as: - Finite automata can be represented by input tape and finite control.

Finite control: The finite control decides the next state on receiving particular input from input tape. The tape reader reads the cells one by one from left to right, and at a time only one input symbol is read.

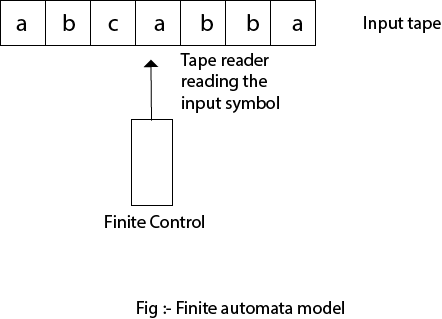
Types of Automata:-

There are two types of finite automata:

Some important points about DFA and NFA:

Q.9) what is the simulation of DFA and NFA ?

Sol : Let N = (QN , Σ, δN , qN0 , FN ) be a NFA. The equivalent DFA D1 is obtained from the so-called subset construction (also called “power construction”).

  We define D = (QD, Σ, δD, qD0 , FD),

Where

●      The alphabet of D is that of N.

●      The states of D are sets of states of N:

QD = P(QN )

●      The initial state qD0 of D is {qN0 }.

●      The final states of D are those sets that contain the final state of N:

FD = {S ∈ P(QN )|  S ∩ FN 6= ∅}

●      The transition function of D arises from the transition function of N as follows:

δD(S, a) = Uq∈S δN (q, a)

That is, δD(S, a) is the set of all states of N that are reachable from some state q via a.

Proposition. For every NFA N, there is a DFA D such that L(D) = L(N)

Q.10) Describe Transition table n Transition diagram ?

Sol : Transition Table :- The transition table is basically a tabular representation of the transition function. It takes two arguments (a state and a symbol) and returns a state (the "next state").

A transition table is represented by the following things:

Transition Diagram :- A transition diagram or state transition diagram is a directed graph which can be constructed as follows:

Unit -1

Basic Concepts and Automata Theory

Q .1) Difference between DFA and NFA?

Sol:

Q.2) what is the application of Finite Automata ?

Sol : Application of Finite Automata is :

1. Finite Automata (FA) –

●      Used in text editors.

●      For the implementation of spell checkers.

2. Push Down Automata (PDA) –

●      For designing the parsing phase of a compiler (Syntax Analysis).

●      For evaluating the arithmetic expressions.

3. Linear Bounded Automata (LBA) –

●      For implementation of genetic programming.

●      For constructing syntactic parse trees for semantic analysis of the compiler.

4. Turing Machine (TM) –

●      For implementation of neural networks and Robotics Applications.

●      For implementation of artificial intelligence.

Q.3)  How to convert NFA to DFA ?

Sol : In NFA, the device goes to multiple states when a particular input is given to the current state. On a given input symbol, it can have zero, one or more than a move. On the other hand, in DFA, the program goes to only one state when a particular input is given to the current state. On a given input symbol, a DFA has only one move.

Let, M = (Q, ∑, δ, q0, F) is an NFA which accepts the language L(M). There should be equivalent DFA denoted by M' = (Q', ∑', q0', δ', F') such that L(M) = L(M')

Steps for Converting NFA to DFA -

Step 1: Initially Q' = ϕ

Step 2: Add q0 of NFA to Q'. Then find the transitions from this start state.

Step 3: In Q', find the possible set of states for each input symbol. If this set of states is not in Q', then add it to Q'.

Step 4: In DFA, the final state will be all the states which contain F(final states of NFA)

Q.4) Write the steps for converting from Mealy Machine to Moore Machine ?

Sol: The output is connected with each state in the Moore machine and the output is given across the edge with an input symbol in the Mealy machine. State output symbols are distributed to the input symbol paths to convert the Moore machine to the Mealy machine. But we will create a separate state for and new output symbol when converting the Mealy machine to Moore machine and are distributed according to incoming and outgoing edges.

The following steps are used for converting Mealy machine to the Moore machine:

Step 1: For each state(Qi), calculate the number of different outputs that are available in the transition table of the Mealy machine.

Step 2: Copy state Qi, if all the outputs of Qi are the same. Break qi into n states as Qin, if it has n distinct outputs where n = 0, 1, 2....

Step 3: If the output of initial state is 0, insert a new initial state at the starting which gives 1 output.

Q.5) For the given set make Transition Diagram and Transition Table for DFA ?

1.     Q = {q0, q1, q2} 

2.     ∑ = {0,1} 

3.     q0 = {q0} 

4.     F = {q2} 

Sol :  Transition Diagram :

Transition Table :

Q.6) Convert the given Moore machine into its equivalent Mealy machine?

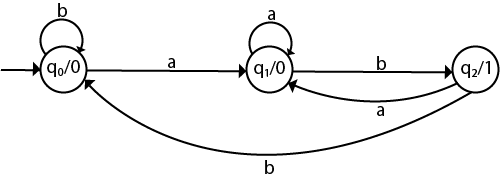
Sol : The transition table of given Moore machine is as follows:

The equivalent Mealy machine can be obtained as follows:

λ' (q0, a) = λ(δ(q0, a)) 

                = λ(q1) 

                = 0 

λ' (q0, b) = λ(δ(q0, b)) 

                = λ(q0) 

                = 0

The λ for state q1 is as follows:

λ' (q1, a) = λ(δ(q1, a)) 

                = λ(q1) 

                = 0 

λ' (q1, b) = λ(δ(q1, b)) 

                = λ(q2) 

                = 1 

The λ for state q2 is as follows:

λ' (q2, a) = λ(δ(q2, a)) 

                = λ(q1) 

                = 0 

λ' (q2, b) = λ(δ(q2, b)) 

                = λ(q0) 

                = 0 

Hence the transition table for the Mealy machine can be drawn as follows:

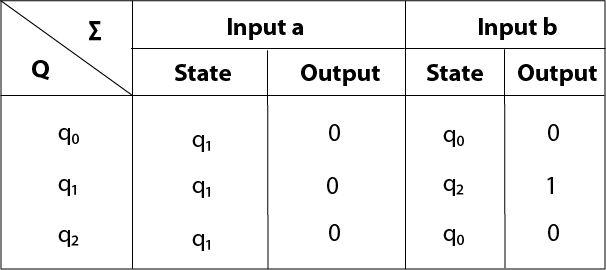
The equivalent Mealy machine will be

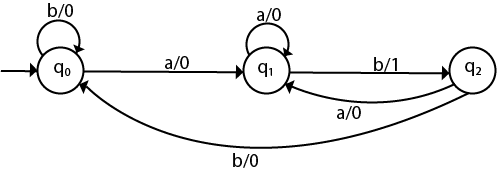
Q.7) What are the advantages and disadvantages of Deterministic Finite Automata (DFA)?

Sol: There are some advantages and disadvantages of DFA,

❖      The union/intersection of the languages recognized by two given DFAs.

❖      The complement of the language recognized by a given DFA.

❖      DFAs were invented to model of a Turing machine, which was too general to study properties of real world machines.

❖      DFAs are one of the most practical models of computation, since there is a trivial linear time, constant-space, online algorithm there are efficient algorithms to find a DFA recognizing.

❖      The classical example of a simply described language that no DFA can recognize is bracket language, i.e language that consists of properly paired brackets such as word "(( )( ))".

❖      On the other hand, finite state automata are of strictly limited power in the

Languages they can recognize; many simple languages, including any

Problem that requires more than constant space to solve, cannot be

Recognized by a DFA.

Q.8) Define Finite Automata in detail  and also define their types ?

Sol:finite automata is :

A finite automaton is a collection of 5-tuple (Q, ∑, δ, q0, F), where:

Finite Automata model are as: - Finite automata can be represented by input tape and finite control.

Finite control: The finite control decides the next state on receiving particular input from input tape. The tape reader reads the cells one by one from left to right, and at a time only one input symbol is read.

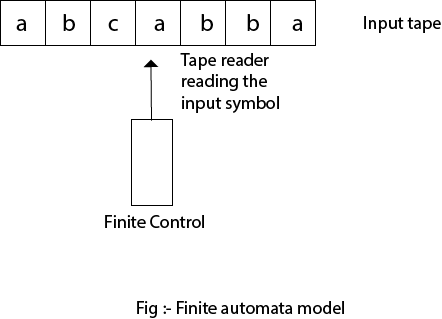
Types of Automata:-

There are two types of finite automata:

Some important points about DFA and NFA:

Q.9) what is the simulation of DFA and NFA ?

Sol : Let N = (QN , Σ, δN , qN0 , FN ) be a NFA. The equivalent DFA D1 is obtained from the so-called subset construction (also called “power construction”).

  We define D = (QD, Σ, δD, qD0 , FD),

Where

●      The alphabet of D is that of N.

●      The states of D are sets of states of N:

QD = P(QN )

●      The initial state qD0 of D is {qN0 }.

●      The final states of D are those sets that contain the final state of N:

FD = {S ∈ P(QN )|  S ∩ FN 6= ∅}

●      The transition function of D arises from the transition function of N as follows:

δD(S, a) = Uq∈S δN (q, a)

That is, δD(S, a) is the set of all states of N that are reachable from some state q via a.

Proposition. For every NFA N, there is a DFA D such that L(D) = L(N)

Q.10) Describe Transition table n Transition diagram ?

Sol : Transition Table :- The transition table is basically a tabular representation of the transition function. It takes two arguments (a state and a symbol) and returns a state (the "next state").

A transition table is represented by the following things:

Transition Diagram :- A transition diagram or state transition diagram is a directed graph which can be constructed as follows: