Unit - 3
Regular and non regular grammar
Q.1) Consider the following statements about the context free grammar
G = {S->SS, S->ab, S->ba, S->ɛ}
I G is ambiguous
II G produces all strings with equal number of a’s and b’s
III G can be accepted by a deterministic PDA
Which combination below expresses all the true statements about G?
1. I only
2. I and III only
3. II and III only
4. I, II and III
Sol: There are different LMD’s for string abab which can be
S =>SS =>SSS =>abSS =>ababS =>abab
S =>SS =>abS =>abab
So the grammar is ambiguous. So statement I is true.
Statement II states that the grammar G produces all strings with equal number of a’s
And b’s but it can’t generate aabb string. So statement II is incorrect.
Statement III is also correct as it can be accepted by deterministic PDA. So correct
Option is (B).
Q.2) Construct a CFG for a given language
L = {wcwR | where w € (a, b)*}
Sol : The string that can be generated for a given language is {aacaa, bcb, abcba, bacab, abbcbba, ....}
The grammar could be:
1. S → aSa rule 1
2. S → bSb rule 2
3. S → c rule 3
Now if we want to derive a string "abbcbba", we can start with start symbols.
1. S → aSa
2. S → abSba from rule 2
3. S → abbSbba from rule 2
4. S → abbcbba from rule 3
Thus any of this kind of string can be derived from the given production rules.
Q.3) Find a reduced grammar equivalent to the grammar G, having production rules, P: S → AC | B, A → a, C → c | BC, E → aA | e
Sol: Phase 1 −
T = { a, c, e }
W1 = { A, C, E } from rules A → a, C → c and E → aA
W2 = { A, C, E } U { S } from rule S → AC
W3 = { A, C, E, S } U ∅
Since W2 = W3, we can derive G’ as −
G’ = { { A, C, E, S }, { a, c, e }, P, {S}}
Where P: S → AC, A → a, C → c , E → aA | e
Phase 2 -
Y1 = { S }
Y2 = { S, A, C } from rule S → AC
Y3 = { S, A, C, a, c } from rules A → a and C → c
Y4 = { S, A, C, a, c }
Since Y3 = Y4, we can derive G” as −
G” = { { A, C, S }, { a, c }, P, {S}}
Where P: S → AC, A → a, C → c
Q.4) Write an algorithm to convert CFG into GNF ?
Sol : Algorithm to convert CFG into GNF, are -
Step 1 − If the start symbol S occurs on some right side, create a new start
Symbol S’ and a new production S’ → S.
Step 2 − Remove Null productions. (Using the Null production removal algorithm
Discussed earlier)
Step 3 − Remove unit productions. (Using the Unit production removal algorithm
Discussed earlier)
Step 4 − Remove all direct and indirect left-recursion.
Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.
Q.5) Convert the following CFG into CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
Sol : Here, S does not appear on the right side of any production and there are no unit or
Null productions in the production rule set. So, we can skip Step 1 to Step 3.
Step 4
Now after replacing
X in S → XY | Xo | p
With
MX | m
We obtain
S → mXY | mY | mXo | mo | p.
And after replacing
X in Y → X n | o
With the right side of
X → mX | m
We obtain
Y → mXn | mn | o.
Two new productions O → o and P → p are added to the production set and then
We came to the final GNF as the following −
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
Q.6) Define the context free grammar(CFG) ?
Sol: A context free grammar (CFG) is in Chomsky normal form (CNF) if all production rules satisfy one of the following conditions:
➔ A non-terminal generating a terminal (e.g.; X->x)
➔ A non-terminal generating two non-terminals (e.g.; X->YZ)
➔ Start symbol generating ε. (e.g.; S->ε)
Consider the following grammars,
G1 = {S->a, S->AZ, A->;a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
❏ CNF is a pre-processing step used in various algorithms.
❏ For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.
Context-free grammar G can be defined as:
G = (V, T, P, S)
Where
G - grammar, used for generate string,
V - final set of non terminal symbol, which are denoted by capital letters,
T - final set of terminal symbol, which are denoted be small letters,
P - set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)
S - start symbol, which is used for derive the string
Q.7) What is the Ambiguity in CFG ?
Sol: Suppose we have a context free grammar G with production rules: S->aSb|bSa|SS|ɛ
Left most derivation (LMD) and Derivation Tree:
Leftmost derivation of a string from staring symbol S is done by replacing leftmost
Non-terminal symbol by RHS of corresponding production rule.
For example: The leftmost derivation of string abab from grammar G above is done
As:
S =>aSb =>abSab =>abab
The symbols in bold are replaced using production rules.
Right most derivation (RMD):
It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.
For Example: The rightmost derivation of string abab from grammar G above
Is done as:
S =>SS =>SaSb =>Sab =>aSbab =>abab
The symbols in bold are replaced using production rules.
A derivation can be either LMD or RMD or both or none. For Example:
S =>aSb =>abSab =>abab is LMD as well as RMD
But S =>SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.
Q.8) Draw a derivation tree for the string "bab" from the CFG given by
S → bSb | a | b
Sol : Now, the derivation tree for the string "bbabb" is as follows:
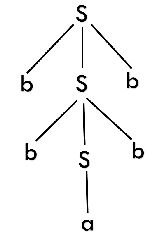
The above tree is a derivation tree drawn for deriving a string bbabb. By simply reading the leaf nodes, we can obtain the desired string. The same tree can also be denoted by
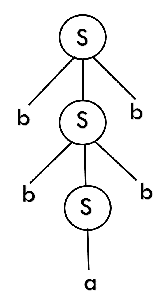
Q.9) what is the unambiguous grammar ?
Sol: A grammar can be unambiguous if the grammar does not contain ambiguity that means if it does not contain more than one leftmost derivation or more than one rightmost derivation or more than one parse tree for the given input string.
To convert ambiguous grammar to unambiguous grammar, we will apply the following rules:
- If the left associative operators (+, -, *, /) are used in the production rule, then apply left recursion in the production rule. Left recursion means that the leftmost symbol on the right side is the same as the non-terminal on the left side. For example,
X → Xa
B. If the right associative operates(^) is used in the production rule then apply right recursion in the production rule. Right recursion means that the rightmost symbol on the left side is the same as the non-terminal on the right side. For example,
X → aX
Q.10) Construct the CFG for the language having any number of a's over the set ∑={a}
Sol: As we know the regular expression for the above language is
r.e. = a*
Production rule for the Regular expression is as follows:
1. S → aS rule 1
2. S → ε rule 2
Now if we want to derive a string "aaaaaa", we can start with start symbols.
S
AS
AaS rule 1
AaaS rule 1
AaaaS rule 1
AaaaaS rule 1
AaaaaaS rule 1
Aaaaaaε rule 2
Aaaaaa
The r.e. = a* can generate a set of strings {ε, a, aa, aaa,.....}. We can have a null string because S is a start symbol and rule 2 gives S → ε.
Q.11) describe the different normal forms ?
Sol : different normal forms -
➢ Chomsky Normal Form(CNF)
A context free grammar (CFG) is in Chomsky normal form (CNF) if all production rules satisfy one of the following conditions:
➔ A non-terminal generating a terminal (e.g.; X->x)
➔ A non-terminal generating two non-terminals (e.g.; X->YZ)
➔ Start symbol generating ε. (e.g.; S->ε)
Consider the following grammars,
G1 = {S->a, S->AZ, A->;a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
➢ Greibach Normal Form (GNF)
A CFG is in Greibach Normal Form if the Productions are in the following forms −
A → b
A → bD 1 …D n
S → ε
Where A, D 1 ,....,D n are non-terminals and b is a terminal.
Algorithm to Convert a CFG into Greibach Normal Form
Step 1 − If the start symbol S occurs on some right side, create a new start
Symbol S’ and a new production S’ → S.
Step 2 − Remove Null productions.
Step 3 − Remove unit productions.
Step 4 − Remove all direct and indirect left-recursion.
Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.
Unit - 3
Regular and non regular grammar
Q.1) Consider the following statements about the context free grammar
G = {S->SS, S->ab, S->ba, S->ɛ}
I G is ambiguous
II G produces all strings with equal number of a’s and b’s
III G can be accepted by a deterministic PDA
Which combination below expresses all the true statements about G?
1. I only
2. I and III only
3. II and III only
4. I, II and III
Sol: There are different LMD’s for string abab which can be
S =>SS =>SSS =>abSS =>ababS =>abab
S =>SS =>abS =>abab
So the grammar is ambiguous. So statement I is true.
Statement II states that the grammar G produces all strings with equal number of a’s
And b’s but it can’t generate aabb string. So statement II is incorrect.
Statement III is also correct as it can be accepted by deterministic PDA. So correct
Option is (B).
Q.2) Construct a CFG for a given language
L = {wcwR | where w € (a, b)*}
Sol : The string that can be generated for a given language is {aacaa, bcb, abcba, bacab, abbcbba, ....}
The grammar could be:
1. S → aSa rule 1
2. S → bSb rule 2
3. S → c rule 3
Now if we want to derive a string "abbcbba", we can start with start symbols.
1. S → aSa
2. S → abSba from rule 2
3. S → abbSbba from rule 2
4. S → abbcbba from rule 3
Thus any of this kind of string can be derived from the given production rules.
Q.3) Find a reduced grammar equivalent to the grammar G, having production rules, P: S → AC | B, A → a, C → c | BC, E → aA | e
Sol: Phase 1 −
T = { a, c, e }
W1 = { A, C, E } from rules A → a, C → c and E → aA
W2 = { A, C, E } U { S } from rule S → AC
W3 = { A, C, E, S } U ∅
Since W2 = W3, we can derive G’ as −
G’ = { { A, C, E, S }, { a, c, e }, P, {S}}
Where P: S → AC, A → a, C → c , E → aA | e
Phase 2 -
Y1 = { S }
Y2 = { S, A, C } from rule S → AC
Y3 = { S, A, C, a, c } from rules A → a and C → c
Y4 = { S, A, C, a, c }
Since Y3 = Y4, we can derive G” as −
G” = { { A, C, S }, { a, c }, P, {S}}
Where P: S → AC, A → a, C → c
Q.4) Write an algorithm to convert CFG into GNF ?
Sol : Algorithm to convert CFG into GNF, are -
Step 1 − If the start symbol S occurs on some right side, create a new start
Symbol S’ and a new production S’ → S.
Step 2 − Remove Null productions. (Using the Null production removal algorithm
Discussed earlier)
Step 3 − Remove unit productions. (Using the Unit production removal algorithm
Discussed earlier)
Step 4 − Remove all direct and indirect left-recursion.
Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.
Q.5) Convert the following CFG into CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
Sol : Here, S does not appear on the right side of any production and there are no unit or
Null productions in the production rule set. So, we can skip Step 1 to Step 3.
Step 4
Now after replacing
X in S → XY | Xo | p
With
MX | m
We obtain
S → mXY | mY | mXo | mo | p.
And after replacing
X in Y → X n | o
With the right side of
X → mX | m
We obtain
Y → mXn | mn | o.
Two new productions O → o and P → p are added to the production set and then
We came to the final GNF as the following −
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
Q.6) Define the context free grammar(CFG) ?
Sol: A context free grammar (CFG) is in Chomsky normal form (CNF) if all production rules satisfy one of the following conditions:
➔ A non-terminal generating a terminal (e.g.; X->x)
➔ A non-terminal generating two non-terminals (e.g.; X->YZ)
➔ Start symbol generating ε. (e.g.; S->ε)
Consider the following grammars,
G1 = {S->a, S->AZ, A->;a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
❏ CNF is a pre-processing step used in various algorithms.
❏ For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.
Context-free grammar G can be defined as:
G = (V, T, P, S)
Where
G - grammar, used for generate string,
V - final set of non terminal symbol, which are denoted by capital letters,
T - final set of terminal symbol, which are denoted be small letters,
P - set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)
S - start symbol, which is used for derive the string
Q.7) What is the Ambiguity in CFG ?
Sol: Suppose we have a context free grammar G with production rules: S->aSb|bSa|SS|ɛ
Left most derivation (LMD) and Derivation Tree:
Leftmost derivation of a string from staring symbol S is done by replacing leftmost
Non-terminal symbol by RHS of corresponding production rule.
For example: The leftmost derivation of string abab from grammar G above is done
As:
S =>aSb =>abSab =>abab
The symbols in bold are replaced using production rules.
Right most derivation (RMD):
It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.
For Example: The rightmost derivation of string abab from grammar G above
Is done as:
S =>SS =>SaSb =>Sab =>aSbab =>abab
The symbols in bold are replaced using production rules.
A derivation can be either LMD or RMD or both or none. For Example:
S =>aSb =>abSab =>abab is LMD as well as RMD
But S =>SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.
Q.8) Draw a derivation tree for the string "bab" from the CFG given by
S → bSb | a | b
Sol : Now, the derivation tree for the string "bbabb" is as follows:
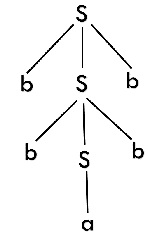
The above tree is a derivation tree drawn for deriving a string bbabb. By simply reading the leaf nodes, we can obtain the desired string. The same tree can also be denoted by
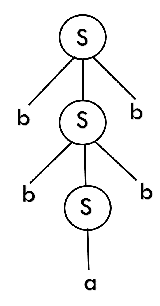
Q.9) what is the unambiguous grammar ?
Sol: A grammar can be unambiguous if the grammar does not contain ambiguity that means if it does not contain more than one leftmost derivation or more than one rightmost derivation or more than one parse tree for the given input string.
To convert ambiguous grammar to unambiguous grammar, we will apply the following rules:
- If the left associative operators (+, -, *, /) are used in the production rule, then apply left recursion in the production rule. Left recursion means that the leftmost symbol on the right side is the same as the non-terminal on the left side. For example,
X → Xa
B. If the right associative operates(^) is used in the production rule then apply right recursion in the production rule. Right recursion means that the rightmost symbol on the left side is the same as the non-terminal on the right side. For example,
X → aX
Q.10) Construct the CFG for the language having any number of a's over the set ∑={a}
Sol: As we know the regular expression for the above language is
r.e. = a*
Production rule for the Regular expression is as follows:
1. S → aS rule 1
2. S → ε rule 2
Now if we want to derive a string "aaaaaa", we can start with start symbols.
S
AS
AaS rule 1
AaaS rule 1
AaaaS rule 1
AaaaaS rule 1
AaaaaaS rule 1
Aaaaaaε rule 2
Aaaaaa
The r.e. = a* can generate a set of strings {ε, a, aa, aaa,.....}. We can have a null string because S is a start symbol and rule 2 gives S → ε.
Q.11) describe the different normal forms ?
Sol : different normal forms -
➢ Chomsky Normal Form(CNF)
A context free grammar (CFG) is in Chomsky normal form (CNF) if all production rules satisfy one of the following conditions:
➔ A non-terminal generating a terminal (e.g.; X->x)
➔ A non-terminal generating two non-terminals (e.g.; X->YZ)
➔ Start symbol generating ε. (e.g.; S->ε)
Consider the following grammars,
G1 = {S->a, S->AZ, A->;a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
➢ Greibach Normal Form (GNF)
A CFG is in Greibach Normal Form if the Productions are in the following forms −
A → b
A → bD 1 …D n
S → ε
Where A, D 1 ,....,D n are non-terminals and b is a terminal.
Algorithm to Convert a CFG into Greibach Normal Form
Step 1 − If the start symbol S occurs on some right side, create a new start
Symbol S’ and a new production S’ → S.
Step 2 − Remove Null productions.
Step 3 − Remove unit productions.
Step 4 − Remove all direct and indirect left-recursion.
Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.