Unit - 4

Push Down Automata and Properties of Context Free Languages

Q. 1) write the properties of CFL ?

Sol :  They are closed under −

●      Union

●      Concatenation

●      Kleene Star operation

Union

Let A 1  and A 2  be two context free languages. Then A 1  ∪ A 2  is also context free.

Example

Let A 1  = { x n y n  , n > 0}. Corresponding grammar G 1  will have P: S1 →aAb|ab

Let A 2  = { c m d m  , m ≥ 0}. Corresponding grammar G 2  will have P: S2 → cBb| ε

Union of A 1  and A 2 , A = A 1  ∪ A 2  = { x n y n  } ∪ { c m d m  }

The corresponding grammar G will have the additional production S → S1 | S2

Concatenation

If A 1  and A 2  are context free languages, then A 1 A 2  is also context free.

Example

Union of the languages A  and A2 , A = A1 A2  = { an bn cm dm }

The corresponding grammar G will have the additional production S → S1 S2

Kleene Star

If A is a context free language, then A* is also context free.

Example

Let A = { xn yn  , n ≥ 0}. Corresponding grammar G will have P: S → aAb| ε

Kleene Star L 1  = { xn yn  }*

The corresponding grammar G 1  will have additional productions S1 → SS 1  | ε

Context-free languages are not closed under −

●      Intersection − If A1 and A2 are context free languages, then A1 ∩ A2 is not necessarily context free.

●      Intersection with Regular Language − If A1 is a regular language and A2 is a context free language, then A1 ∩ A2 is a context free language.

●      Complement − If A1 is a context free language, then A1’ may not be context free.

Q.2 ) Convert the following grammar to a PDA that accepts the same language.

1.     S → 0S1 | A 

2.     A → 1A0 | S | ε 

Sol : The CFG can be first simplified by eliminating unit productions:

S → 0S1 | 1S0 |  ε 

Now we will convert this CFG to GNF:

S → 0SX | 1SY |  ε 

X → 1 

Y → 0 

The PDA can be:

R1: δ(q, ε, S) = {(q, 0SX) | (q, 1SY) | (q, ε)}

R2: δ(q, ε, X) = {(q, 1)}

R3: δ(q, ε, Y) = {(q, 0)}

R4: δ(q, 0, 0) = {(q, ε)}

R5: δ(q, 1, 1) = {(q, ε)}

Q. 3) Construct PDA for the given CFG, and test whether 0104 is acceptable by this PDA.

1.     S → 0BB 

2.     B → 0S | 1S | 0

Sol : The PDA can be given as:

A = {(q), (0, 1), (S, B, 0, 1), δ, q, S, ?} 

The production rule δ can be:

R1: δ(q, ε, S) = {(q, 0BB)}

R2: δ(q, ε, B) = {(q, 0S) | (q, 1S) | (q, 0)}

R3: δ(q, 0, 0) = {(q, ε)}

R4: δ(q, 1, 1) = {(q, ε)}

Testing 0104 i.e. 010000 against PDA:

δ(q, 010000, S) ⊢ δ(q, 010000, 0BB) 

                ⊢ δ(q, 10000, BB)              R1 

                ⊢ δ(q, 10000,1SB)              R3   

                ⊢ δ(q, 0000, SB)               R2       

                ⊢ δ(q, 0000, 0BBB)             R1    

                ⊢ δ(q, 000, BBB)               R3       

                ⊢ δ(q, 000, 0BB)               R2     

                ⊢ δ(q, 00, BB)                 R3    

                ⊢ δ(q, 00, 0B)                 R2   

                ⊢ δ(q, 0, B)                   R3   

                ⊢ δ(q, 0, 0)                   R2 

                ⊢ δ(q, ε)                      R3   

                ACCEPT 

Thus 0104 is accepted by the PDA .

Q. 4) Define Pushdown automata (PDA) in detail ?

Sol : It is a way to implement a context-free grammar as we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.

Basically a pushdown automaton is -

“Finite state machine” + “a stack”

A pushdown automaton has three components −

●      an input tape,

●      a control unit, and

●      a stack with infinite size.

The stack head scans the top symbol of the stack.

A stack does two operations −

●      Push − a new symbol is added at the top.

●      Pop − the top symbol is read and removed.

A PDA may or may not read an input symbol, but it has to read the top of the stack in every transition.

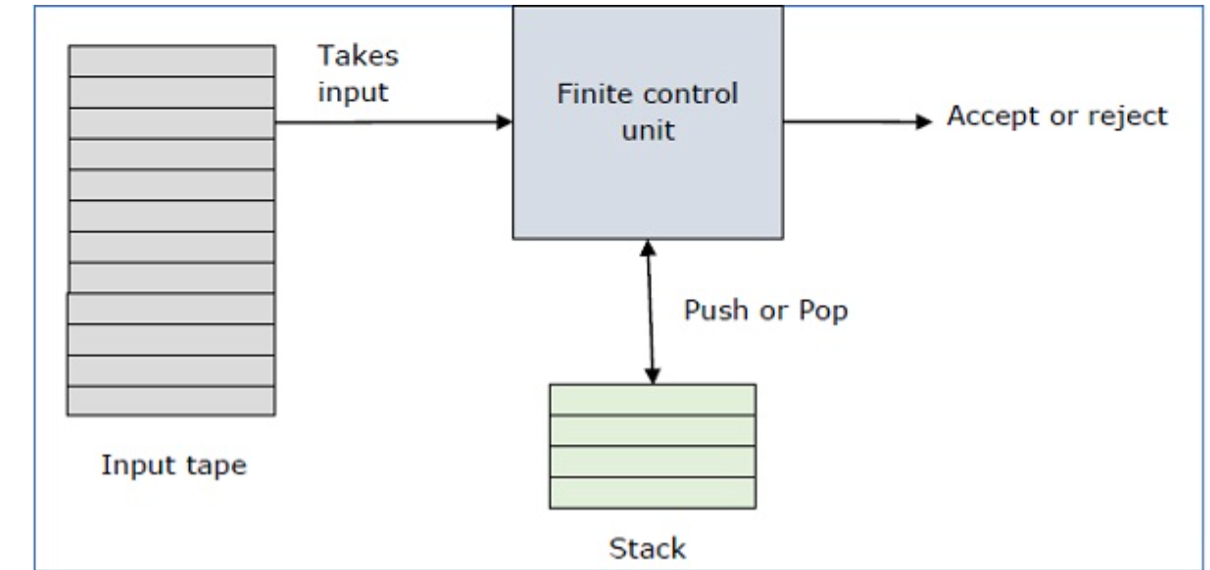
A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q 0 , I, F) −

●      Q is the finite number of states

●      ∑ is input alphabet

●      S is stack symbols

●      δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S*

●      q 0  is the initial state (q 0  ∈ Q)

●      I is the initial stack top symbol (I ∈ S)

●      F is a set of accepting states (F ∈ Q)

The following diagram shows a transition in a PDA from a state q 1  to state q 2 , labeled as a,b → c −

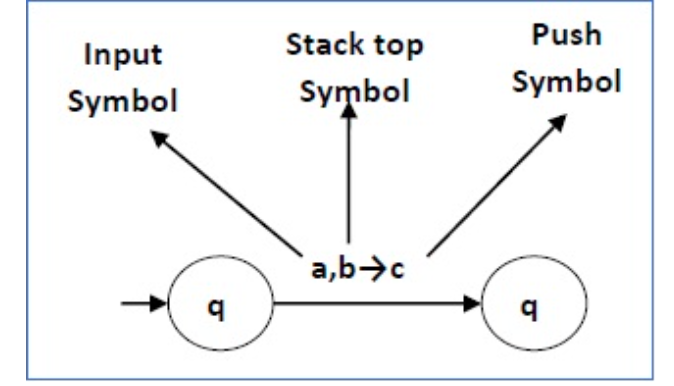
This means at state q 1 , if we encounter an input string ‘a’ and top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q 2 .

Q.5 ) What is Deterministic PDA’s  ?

Sol : Deterministic PDA -

●      Machine transitions are based on the current state and input symbol, and also the current topmost symbol of the stack.

●      Symbols lower in the stack are not visible and have no immediate effect. Machine actions include pushing, popping, or replacing the stack top.

●      A deterministic pushdown automaton has at most one legal transition for the same combination of input symbol, state, and top stack symbol.

●      This is where it differs from the nondeterministic pushdown automaton.

A PDA M can be defined as 7 tuples -

M = (Q, ∑, T, q0, Z0, A, δ)

Where,

●      Q is finite set of states,

●      ∑ is finite set of input symbol,

●      T is a finite set of stack symbol,

●      q0 ∈ Q is a start state,

●      Z0 ∈ T is the starting stack symbol,

●      A ⊆ Q, where A is a set of accepting states,

●      δ is a transition function, where :

δ :(Q X ( ∑ U {ε }) X  T ) ➝ p(Q  X T* )

Q.6 ) What is the two stack automata, explain ?

Sol : Two stack automata -

A computational model based on the generalization of Pushdown Automata(PDA) is the Two-Stack PDA.

A deterministic two-stack PDA is equal to a non-deterministic two-stack PDA.

The move of the Two-Stack PDA is based on

●      The state of the finite control.

●      The input symbol read.

●      The top stack symbol on each of its stacks.

A Turing machine can accept languages not accepted by any PDA with one stack.

The strength of pushdown automata can be increased by adding additional (extra) stacks.

Actually, a PDA with two stacks has the same computation power as a Turing Machine.

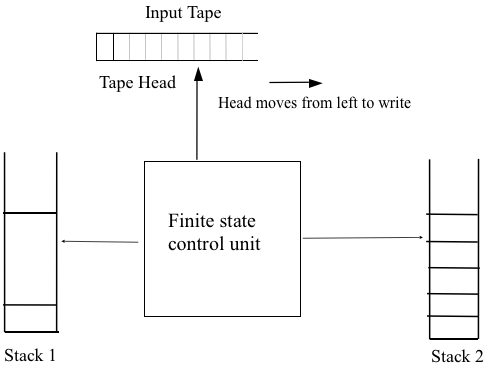
Fig : two stack PDA

Q.7 ) what do you mean by context free grammar ?

Sol : We may construct an equivalent non-deterministic PDA if a grammar G is context-free, which accepts the language generated by the context-free grammar G. For Grammar G, a parser can be constructed.

When P is a pushdown automata, and G is context free grammar can be constructed, where

L(G) = L(P)

Algorithm to find PDA corresponding to a given CFG

Input − A CFG, G = (V, T, P, S)

Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F)

Step 1 − Convert the productions of the CFG into GNF.

Step 2 − The PDA will have only one state {q}.

Step 3 − The start symbol of CFG will be the start symbol in the PDA.

Step 4 − All non-terminals of the CFG will be the stack symbols of the PDA and all the terminals of the CFG will be the input symbols of the PDA.

Step 5 − For each production in the form A → aX where a is terminal and A, X are combination of terminal and non-terminals, make a transition δ (q, a, A)

Q.8 ) Design PDA for Palindrome strips ?

Sol : Suppose the language consists of string

L = {aba, aa, bb, bab, bbabb, aabaa, ......].

The string can be odd palindrome or even palindrome. The logic for constructing

PDA is that we will push a symbol onto the stack till half of the string then we will

Read each symbol and then perform the pop operation. We will compare to see

Whether the symbol which is popped is similar to the symbol which is read. Whether

When we reach the end of the input, we expect the stack to be empty.

This PDA is a non-deterministic PDA because finding the mid for the given string and

Reading the string from left and matching it with from right (reverse) direction leads to non-deterministic moves.

Here is the ID

1. δ(q1, a, Z) = (q1, aZ)   
2. δ(q0, b, Z) = (q1,bZ)
3. δ(q0, a, a) = (q1,aa)
4. δ(q1, a, b) = (q1, ab)
5. δ(q1, a, b) = (q1, ba)
6. δ(q1, b, b) = (q1, bb)

(pushing the symbol onto the stack)

7.     δ(q1, a, a) =  (q2, ε)

8.     δ(q1, b, b) = (q2, ε)

9.     δ(q2, a, a) = (q2, ε)

10. δ(q2, b, b) = (q2, ε)

11. δ(q2, ε, Z) = (q2, ε)

(popping the symbol on reading the same kind of symbol)

Simulation of abaaba

1. δ(q1, abaaba, Z)            Apply rule 1 
2. ⊢ δ(q1, baaba, aZ)          Apply rule 5 
3. ⊢ δ(q1, aaba, baZ)          Apply rule 4 
4. ⊢ δ(q1, aba, abaZ)          Apply rule 7 
5. ⊢ δ(q2, ba, baZ)            Apply rule 8 
6. ⊢ δ(q2, a, aZ)              Apply rule 7 
7. ⊢ δ(q2, ε, Z)               Apply rule 11 
8. ⊢ δ(q2, ε)                  Accept

Q.9 ) Convert the given grammar to a PDA that accepts the same language.

1.     S → 0S1 | A 

2.     A → 1A0 | S | ε 

Sol : To simplify the above grammar eliminating unit production in CFG :

S → 0S1 | 1S0 |  ε

Here , we convert the CFG to GNF :

1.     S → 0SX | 1SY |  ε 

2.     X → 1 

3.     Y → 0 

The final PDA can be :

R1: δ(q, ε, S) = {(q, 0SX) | (q, 1SY) | (q, ε)}

R2: δ(q, ε, X) = {(q, 1)}

R3: δ(q, ε, Y) = {(q, 0)}

R4: δ(q, 0, 0) = {(q, ε)}

R5: δ(q, 1, 1) = {(q, ε)}

Q.10 ) Define the Non- deterministic pushdown Automata ?

Sol : Non deterministic Pushdown Automata

●      Non deterministic pushdown automata are quite similar to the NFA.

●      Non-deterministic PDAs are also approved by the CFG that accepts deterministic PDAs.

●      Similarly, there are several CFGs that only NPDA and not DPDA can consider. Therefore, NPDA is more efficient than DPDA.

●      Non deterministic pushdown automat is basically an non finite automata (nfa) with a stack added to it.

Nondeterministic pushdown automaton or npda is a 7-tuple -

M = (Q, ∑, T, δ , q0, z, F)

Where

●      Q is a finite set of states,

●      ∑ is a the input alphabet,

●      T is the stack alphabet,

●      δ is a transition function,

●      q0 ∈   Q is the initial state,

●      z  ∈  T is the stack start symbol, and

●      F ⊆ Q is a set of final states.

Unit - 4

Push Down Automata and Properties of Context Free Languages

Q. 1) write the properties of CFL ?

Sol :  They are closed under −

●      Union

●      Concatenation

●      Kleene Star operation

Union

Let A 1  and A 2  be two context free languages. Then A 1  ∪ A 2  is also context free.

Example

Let A 1  = { x n y n  , n > 0}. Corresponding grammar G 1  will have P: S1 →aAb|ab

Let A 2  = { c m d m  , m ≥ 0}. Corresponding grammar G 2  will have P: S2 → cBb| ε

Union of A 1  and A 2 , A = A 1  ∪ A 2  = { x n y n  } ∪ { c m d m  }

The corresponding grammar G will have the additional production S → S1 | S2

Concatenation

If A 1  and A 2  are context free languages, then A 1 A 2  is also context free.

Example

Union of the languages A  and A2 , A = A1 A2  = { an bn cm dm }

The corresponding grammar G will have the additional production S → S1 S2

Kleene Star

If A is a context free language, then A* is also context free.

Example

Let A = { xn yn  , n ≥ 0}. Corresponding grammar G will have P: S → aAb| ε

Kleene Star L 1  = { xn yn  }*

The corresponding grammar G 1  will have additional productions S1 → SS 1  | ε

Context-free languages are not closed under −

●      Intersection − If A1 and A2 are context free languages, then A1 ∩ A2 is not necessarily context free.

●      Intersection with Regular Language − If A1 is a regular language and A2 is a context free language, then A1 ∩ A2 is a context free language.

●      Complement − If A1 is a context free language, then A1’ may not be context free.

Q.2 ) Convert the following grammar to a PDA that accepts the same language.

1.     S → 0S1 | A 

2.     A → 1A0 | S | ε 

Sol : The CFG can be first simplified by eliminating unit productions:

S → 0S1 | 1S0 |  ε 

Now we will convert this CFG to GNF:

S → 0SX | 1SY |  ε 

X → 1 

Y → 0 

The PDA can be:

R1: δ(q, ε, S) = {(q, 0SX) | (q, 1SY) | (q, ε)}

R2: δ(q, ε, X) = {(q, 1)}

R3: δ(q, ε, Y) = {(q, 0)}

R4: δ(q, 0, 0) = {(q, ε)}

R5: δ(q, 1, 1) = {(q, ε)}

Q. 3) Construct PDA for the given CFG, and test whether 0104 is acceptable by this PDA.

1.     S → 0BB 

2.     B → 0S | 1S | 0

Sol : The PDA can be given as:

A = {(q), (0, 1), (S, B, 0, 1), δ, q, S, ?} 

The production rule δ can be:

R1: δ(q, ε, S) = {(q, 0BB)}

R2: δ(q, ε, B) = {(q, 0S) | (q, 1S) | (q, 0)}

R3: δ(q, 0, 0) = {(q, ε)}

R4: δ(q, 1, 1) = {(q, ε)}

Testing 0104 i.e. 010000 against PDA:

δ(q, 010000, S) ⊢ δ(q, 010000, 0BB) 

                ⊢ δ(q, 10000, BB)              R1 

                ⊢ δ(q, 10000,1SB)              R3   

                ⊢ δ(q, 0000, SB)               R2       

                ⊢ δ(q, 0000, 0BBB)             R1    

                ⊢ δ(q, 000, BBB)               R3       

                ⊢ δ(q, 000, 0BB)               R2     

                ⊢ δ(q, 00, BB)                 R3    

                ⊢ δ(q, 00, 0B)                 R2   

                ⊢ δ(q, 0, B)                   R3   

                ⊢ δ(q, 0, 0)                   R2 

                ⊢ δ(q, ε)                      R3   

                ACCEPT 

Thus 0104 is accepted by the PDA .

Q. 4) Define Pushdown automata (PDA) in detail ?

Sol : It is a way to implement a context-free grammar as we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.

Basically a pushdown automaton is -

“Finite state machine” + “a stack”

A pushdown automaton has three components −

●      an input tape,

●      a control unit, and

●      a stack with infinite size.

The stack head scans the top symbol of the stack.

A stack does two operations −

●      Push − a new symbol is added at the top.

●      Pop − the top symbol is read and removed.

A PDA may or may not read an input symbol, but it has to read the top of the stack in every transition.

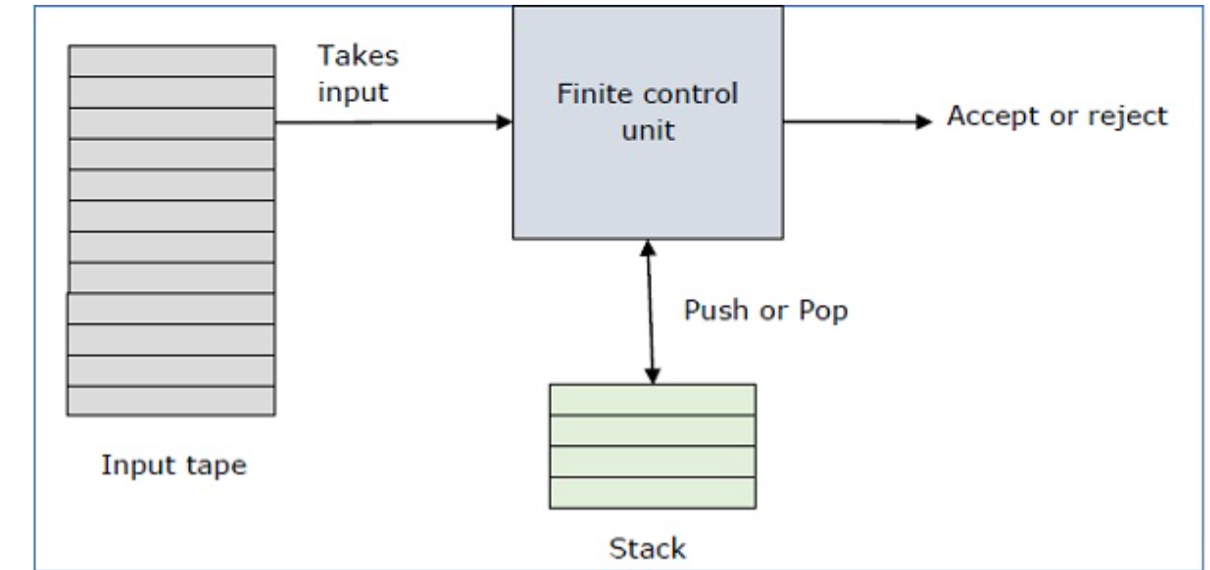
A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q 0 , I, F) −

●      Q is the finite number of states

●      ∑ is input alphabet

●      S is stack symbols

●      δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S*

●      q 0  is the initial state (q 0  ∈ Q)

●      I is the initial stack top symbol (I ∈ S)

●      F is a set of accepting states (F ∈ Q)

The following diagram shows a transition in a PDA from a state q 1  to state q 2 , labeled as a,b → c −

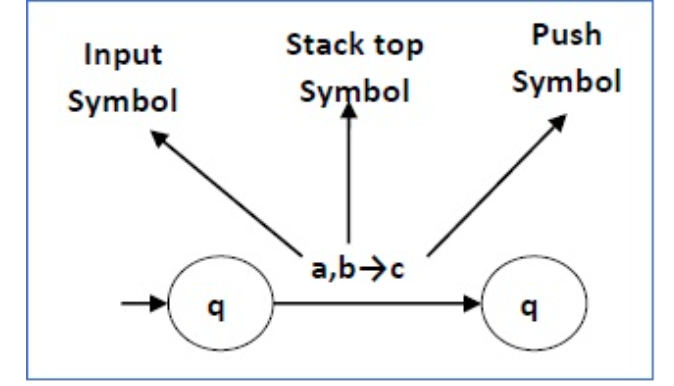
This means at state q 1 , if we encounter an input string ‘a’ and top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q 2 .

Q.5 ) What is Deterministic PDA’s  ?

Sol : Deterministic PDA -

●      Machine transitions are based on the current state and input symbol, and also the current topmost symbol of the stack.

●      Symbols lower in the stack are not visible and have no immediate effect. Machine actions include pushing, popping, or replacing the stack top.

●      A deterministic pushdown automaton has at most one legal transition for the same combination of input symbol, state, and top stack symbol.

●      This is where it differs from the nondeterministic pushdown automaton.

A PDA M can be defined as 7 tuples -

M = (Q, ∑, T, q0, Z0, A, δ)

Where,

●      Q is finite set of states,

●      ∑ is finite set of input symbol,

●      T is a finite set of stack symbol,

●      q0 ∈ Q is a start state,

●      Z0 ∈ T is the starting stack symbol,

●      A ⊆ Q, where A is a set of accepting states,

●      δ is a transition function, where :

δ :(Q X ( ∑ U {ε }) X  T ) ➝ p(Q  X T* )

Q.6 ) What is the two stack automata, explain ?

Sol : Two stack automata -

A computational model based on the generalization of Pushdown Automata(PDA) is the Two-Stack PDA.

A deterministic two-stack PDA is equal to a non-deterministic two-stack PDA.

The move of the Two-Stack PDA is based on

●      The state of the finite control.

●      The input symbol read.

●      The top stack symbol on each of its stacks.

A Turing machine can accept languages not accepted by any PDA with one stack.

The strength of pushdown automata can be increased by adding additional (extra) stacks.

Actually, a PDA with two stacks has the same computation power as a Turing Machine.

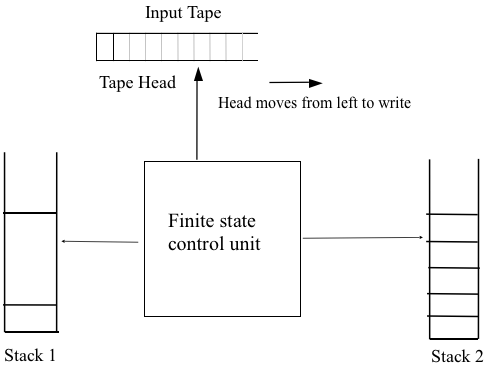
Fig : two stack PDA

Q.7 ) what do you mean by context free grammar ?

Sol : We may construct an equivalent non-deterministic PDA if a grammar G is context-free, which accepts the language generated by the context-free grammar G. For Grammar G, a parser can be constructed.

When P is a pushdown automata, and G is context free grammar can be constructed, where

L(G) = L(P)

Algorithm to find PDA corresponding to a given CFG

Input − A CFG, G = (V, T, P, S)

Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F)

Step 1 − Convert the productions of the CFG into GNF.

Step 2 − The PDA will have only one state {q}.

Step 3 − The start symbol of CFG will be the start symbol in the PDA.

Step 4 − All non-terminals of the CFG will be the stack symbols of the PDA and all the terminals of the CFG will be the input symbols of the PDA.

Step 5 − For each production in the form A → aX where a is terminal and A, X are combination of terminal and non-terminals, make a transition δ (q, a, A)

Q.8 ) Design PDA for Palindrome strips ?

Sol : Suppose the language consists of string

L = {aba, aa, bb, bab, bbabb, aabaa, ......].

The string can be odd palindrome or even palindrome. The logic for constructing

PDA is that we will push a symbol onto the stack till half of the string then we will

Read each symbol and then perform the pop operation. We will compare to see

Whether the symbol which is popped is similar to the symbol which is read. Whether

When we reach the end of the input, we expect the stack to be empty.

This PDA is a non-deterministic PDA because finding the mid for the given string and

Reading the string from left and matching it with from right (reverse) direction leads to non-deterministic moves.

Here is the ID

1. δ(q1, a, Z) = (q1, aZ)   
2. δ(q0, b, Z) = (q1,bZ)
3. δ(q0, a, a) = (q1,aa)
4. δ(q1, a, b) = (q1, ab)
5. δ(q1, a, b) = (q1, ba)
6. δ(q1, b, b) = (q1, bb)

(pushing the symbol onto the stack)

7.     δ(q1, a, a) =  (q2, ε)

8.     δ(q1, b, b) = (q2, ε)

9.     δ(q2, a, a) = (q2, ε)

10. δ(q2, b, b) = (q2, ε)

11. δ(q2, ε, Z) = (q2, ε)

(popping the symbol on reading the same kind of symbol)

Simulation of abaaba

1. δ(q1, abaaba, Z)            Apply rule 1 
2. ⊢ δ(q1, baaba, aZ)          Apply rule 5 
3. ⊢ δ(q1, aaba, baZ)          Apply rule 4 
4. ⊢ δ(q1, aba, abaZ)          Apply rule 7 
5. ⊢ δ(q2, ba, baZ)            Apply rule 8 
6. ⊢ δ(q2, a, aZ)              Apply rule 7 
7. ⊢ δ(q2, ε, Z)               Apply rule 11 
8. ⊢ δ(q2, ε)                  Accept

Q.9 ) Convert the given grammar to a PDA that accepts the same language.

1.     S → 0S1 | A 

2.     A → 1A0 | S | ε 

Sol : To simplify the above grammar eliminating unit production in CFG :

S → 0S1 | 1S0 |  ε

Here , we convert the CFG to GNF :

1.     S → 0SX | 1SY |  ε 

2.     X → 1 

3.     Y → 0 

The final PDA can be :

R1: δ(q, ε, S) = {(q, 0SX) | (q, 1SY) | (q, ε)}

R2: δ(q, ε, X) = {(q, 1)}

R3: δ(q, ε, Y) = {(q, 0)}

R4: δ(q, 0, 0) = {(q, ε)}

R5: δ(q, 1, 1) = {(q, ε)}

Q.10 ) Define the Non- deterministic pushdown Automata ?

Sol : Non deterministic Pushdown Automata

●      Non deterministic pushdown automata are quite similar to the NFA.

●      Non-deterministic PDAs are also approved by the CFG that accepts deterministic PDAs.

●      Similarly, there are several CFGs that only NPDA and not DPDA can consider. Therefore, NPDA is more efficient than DPDA.

●      Non deterministic pushdown automat is basically an non finite automata (nfa) with a stack added to it.

Nondeterministic pushdown automaton or npda is a 7-tuple -

M = (Q, ∑, T, δ , q0, z, F)

Where

●      Q is a finite set of states,

●      ∑ is a the input alphabet,

●      T is the stack alphabet,

●      δ is a transition function,

●      q0 ∈   Q is the initial state,

●      z  ∈  T is the stack start symbol, and

●      F ⊆ Q is a set of final states.