Unit - 5
Turing Machines and Recursive Function Theory
Q.1 ) What is the linear bounded automata ?
Sol : Linear bounded Automata
A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
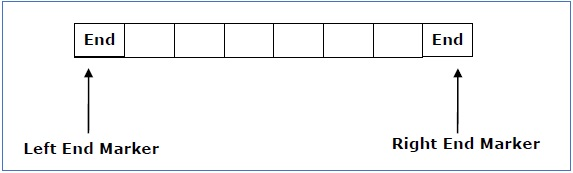
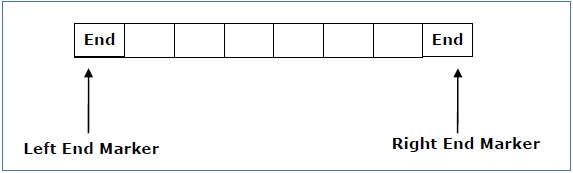
The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.
A linear bounded automata can be defined in 8-tuple -
(Q, X, ∑, q0, ML, MR, δ, F)
Where
● Q is a finite set of states
● X is the tape alphabet
● ∑ is the input alphabet
● q0 is the initial state
● ML is the left end marker
● MR is the right end marker where MR ≠ ML
● δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.
● F is the set of final states.
Q.2 ) Explain the halting problem in turing machine ?
Sol : Halting problem
Input : A turing machine and an input string T.
Problem - Does the Turing machine complete the T-string computation in a finite number of steps? Either yes or no must be the answer.
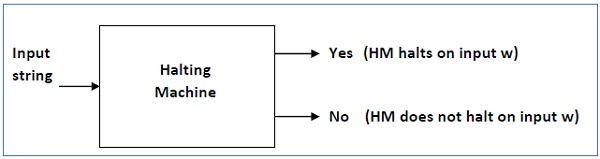
Answer : We will first assume that there is such a Turing machine to solve this problem, and then we will demonstrate that it contradicts itself. This Turing machine would be called a Halting machine that produces in a finite amount of time a 'yes' or no'. The performance comes as 'yes' if the stopping machine finishes in a finite amount of time, otherwise as no'.
The following is a Halting Computer block diagram -
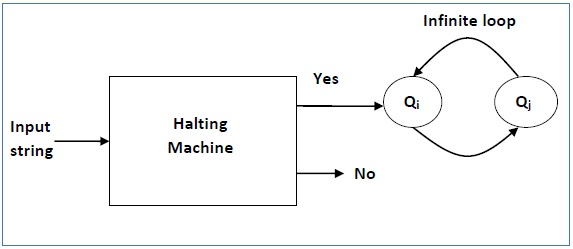
Now we will design an inverted halting machine (HM)’ as -
● If H returns YES, then loop forever.
● If H returns NO, then halt.
Below is the block diagram of inverted halting machine -
In addition, as follows, a machine (HM)2 whose input itself is constructed -
● If - (HM)2 halts on input, loop forever
● Else - halt
Now , we have a contradiction. So , the halting problem is undecidable .
Q.3 ) Describe the church’s thesis ?
Sol : Church’s thesis -
In 1936, a technique named as lambda-calculus was created by Alonzo Church
Within which the Church numerals area unit well outlined, i.e. the encryption of
Natural numbers. Additionally in 1936, mathematician machines (earlier known as
Theoretical model for machines) was created by mathematician, that’s used for
Manipulating the symbols of string with the assistance of tape.
Church mathematician Thesis :
Turing machine is outlined as associate degree abstract illustration of a computer
Like hardware in computers. Mathematician planned Logical Computing Machines
(LCMs), i.e. mathematician’s expressions for Turing Machines. This was done to
Outline algorithms properly. So, Church created a mechanical methodology named
As ‘M’ for manipulation of strings by mistreatment logic and arithmetic.
This methodology M should pass the subsequent statements:
• Number of directions in M should be finite.
• Output ought to be made when playing a finite variety of steps.
• It mustn’t be imagined, i.e. is created in the world.
• It mustn’t need any complicated understanding.
Using these statements Church planned a hypothesis known as Church’s
Mathematician thesis that may be expressed as: “The assumption that the intuitive
Notion of estimable functions is known with partial algorithmic functions.”
In 1930, this statement was initial developed by Alonzo Church and is typically
Brought up as Church’s thesis, or the Church-Turing thesis. However, this hypothesis
Can not be proved.
The algorithmic functions is estimable when taking following assumptions:
- Every and each operate should be estimable.
2. Let ‘F’ be the estimable operate and when playing some elementary operations to ‘F’, it'll rework a replacement operate ‘G’ then this operate ‘G’ mechanically becomes the estimable operate.
3. If any operates that follow on top of 2 assumptions should be states as an estimable function.
Q.4 ) What do you mean by modification of a Turing machine ?
Sol : A typical Turing Machine is a machine that moves either to the left or right when an input is given and it can overwrite the current symbol.
A Turing Machine can be described as a 7-tuple:
( Q, X , * , f, q0 , B, F )
Where,
Q - finite set of state
X - tape alphabet
* - input alphabet
f - transition function
f : Q x X - - > Q x X x { left_shift , right_shift }
q0 - initial state
B - blank symbol
F - set of final state
Some languages, called recursively enumerable languages, can be accepted by a regular Turing machine.
Let's see if we can increase the number of languages recognised by the Turing Machine by doing some form of modification.
- Turing machine with stay option
If the head could still remain in one position without moving anywhere instead of moving left or right on seeing an input, i.e.
f : Q x X - - > Q x X x { left_shift , right_shift }
The number of languages recognised by the Turing machine is still the same.
2. Turing machine with semi - infinite tape
We know that a turing machine has an infinite input tape with extends in both the direction (left or right). So now if we restrict it to extend only in one direction and not in both the directions, i.e. We make the tape semi-infinite, so the number of languages the Turing machine accepts remains the same as well.
3. Offline turing machine
Both the input and output are present on the tape in the traditional turing machine , the head has the power to travel over the input and can alter or change the input , if we don’t want to change the input we can have the input in a separate file, which is ready only then the head can’t make changes to it.
4. Jumping turing machine
The head of the regular Turing machine can move only one step to the right or left, but the head can move not only one step to the left or right if the Turing machine leaps, but it can move more than one step, i.e. 2, 3, 4, 5, 6,... Etc., or it can jump to any cell on the right or left of the input tape.
f : Q x X - - > Q x X x { left_shift , right_shift } x { n }
N is the number of moves we want to pass to the left or right. But the languages accepted by the Turing machine are still similar.
5. Non erasing turing machine
The input symbol can be converted to blank in the regular Turing machine, but if we eliminate this facility to change the input symbol to blank, this type of Turing machine is called a non-erasing Turing machine. We may substitute any other symbol other than blank for the input. The number of languages recognised by the Turing machine remains the same despite this update.
6. Always writing turing machine
Standard Turing machine gives us the power to leave it as it is without making any adjustments when seeing an input, but it is necessary to modify the input once we see it. We can not leave it as it is in always writing Turing machine. But this kind of change did not help to increase the number of languages that the Turing machine approved.
Therefore after making so many changes to the Turing machine, we see that the number of languages recognised by it is still the same. The Turing Machine is thus the most efficient machine.
Q.5 ) What kind of technique is used in a Turing machine construction ?
Sol : There are some technique for turing machine , which are -
● Storage in finite control
Technique: - Using the finite control of a TM to hold a finite amount of data, in addition to the state.
Method: - Assuming the state as [q, A, B, C], for example, when the finite control holds three data elements A, B, and C.
Example:
Design a TM to recognize 01* + 10*. The set of states are of the form [qi, X] where qi = q1, q2; X = 0, 1, B.
• The control portion (state) remembers what the TM is doing (q0 = not read 1st symbol; q1 = reverse).
• The data portion remembers the first symbol seen (0, or 1).
The transition function d is as follows.
• d([q0, B], a) = ([q1, a], a, R) for a = 0, 1. --- Copying the symbol it scanned.
• d([q1, a],a) = ([q1, a],a, R) wherea is the complement of a = 0, 1. --- Skipping symbols which are complements of the 1st symbol read (stored in the state as a).
• d([q1, a], B) = ([q1, B], B, R) for a = 0, 1. --- Entering the accepting state [q, B] when reaching the 1st blank.
● Multi tracks
➢ Assuming the tape of a TM as composed of several tracks.
➢ For example, if there are three tracks, we use the tape symbol as [X, Y, Z]
Example
The TM recognizes the non-CFL language
L = {wcw | w is in (0 + 1)+}.
Que: Why does not the power of the TM increase in this way?
Answer: just a kind of tape symbol labeling.
● Subroutine
Much as a computer programme has a primary procedure and procedure the TM can also be programmed to have subroutines, A core TM and TMs that function as subroutines.
Suppose we're going to make n copies of a word w Input is #w# and the output is #w# w| ww{z. . . w} n times .
In this situation, we can compose the mappings for a TM Msub That ends with #w#xw when launched on #w#x. This is called Msub x times by the key TM.
Likewise, for Multiplying two unary numbers m and n, on m occasions, n must be copied. For copying we can write a sub TM and main TM will name this m times.
The M1 and M2 states must be disjointed in order for a Turing machine M1 to use another Turing machine M2 as a subroutine. The control also goes to the initial state of M2 when M1 wishes to call M2, from the state of M1. When the subroutine stops and returns to M1, from M2's stopping state, the subroutine returns to M2 the computer goes into a certain M1 mode.
Notice that a subroutine TM calls its subroutine another TM (turing machine) This approach helps to construct a TM in a top-down way, separating the job into tasks and writing.
Q.6 ) Explain a Turing machine with some examples ?
Sol : Turing machine -
● A Turing Machine (TM) is a mathematical model which comprises an infinite length tape divided into cells on which input is given.
● It has a head which reads the input tape.
● A state register stores the current state.
● After an input symbol is read, it is replaced by another symbol, its internal state gets changed, and it moves from one cell to the right or left.
● After reaching the final state, the input string is accepted, otherwise rejected.
A TM can be formally described as a 7-tuple (Q, X, ∑, δ, q 0 , B, F)
Where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function; δ : Q × X → Q × X × {Left_shift, Right_shift}.
q 0 is the initial state
B is the blank symbol
F is the set of final states
Example
Turing machine M = (Q, X, ∑, δ, q 0 , B, F) with
Q = {q 0 , q 1 , q 2 , q f }
X = {a, b}
∑ = {1}
q 0 = {q 0 }
B = blank symbol
F = {q f }
δ is given by −
Tape alphabet symbol | Present state ‘q0’ | Present state ‘q1’ | Present state ‘q2’ |
a | 1Rq1 | 1Lq0 | 1Lqf |
b | 1Lq2 | 1Rq1 | 1Rqf |
Here 1Rq 1 write symbol is 1, the tape moves right, and the next state is q 1 . Similarly,
1Lq 2 write symbol is 1, the tape moves left, and the next state is q 2 .
Q.7 ) What do you mean by a Restricted turing machine ?
Sol : Restricted Turing Machine, included -
❖ TM with semi-infinite Tapes
Theorem -
Every language accepted by a TM M2 is also accepted by a TM M1 with the following restriction :
● M1’s head never moves left of it’s initial position
( so the tape is semi - infinite essential)
● M1 never writes a blank.
(M1 and M2 are equivalent .)
❖ Multistack Machine -
● Multistack Machine, which are restricted versions of TM , may be regarded as extension of pushdown automata (PDA’s)
● Actually , a PDA with two stacks has the same computation power as the TM .
● Theorem -
If a language is accepted by TM, then it is accepted by a two - stack machine .
❖ Counter Machine -
● There are two ways to think of a counter machine .
● First , As a multistack machine with each stack replaced by a counter regarded to be on a tape of a TM.
➔ A counter holds any non negative integer.
➔ The machine can only distinguish zero and non zero counters .
➔ The move conduct the following operation :
Changing the state ;
Add or subtract 1 from a counter which cannot become negative.
Q.8 ) What is the undecidable problem about turing machine , give some example also ?
Sol : Undecidable problem about turing machine
The problems for which we cannot make an algorithm that can answer the
Problems correctly in finite time are termed as Undecidable Problems.
- These problems may be partially decidable but they will never be decidable.
- Hence, there will always be a condition that leads the Turing Machine into an
Infinite loop without providing an answer at all.
- This can be explained by Fermat’s Theorem.
- A popular Undecidable Problem which states that no three positive integers a, b
And c for any n>2 can ever satisfy the equation: a^n + b^n = c^n.
- If we feed this problem to a Turing machine to find such a solution which gives a
Contradiction then a Turing Machine might run forever, to find the suitable values
Of n, a, b and c.
- But we are always unsure whether a contradiction exists or not and hence we
Term this problem as an Undecidable Problem.
Example -
These are few important Undecidable Problems:
❏ Whether a CFG generates all the strings or not?
As a CFG generates infinite strings, we can’t ever reach up to the last string and hence it is Undecidable.
❏ Whether two CFG L and M equal?
Since we cannot determine all the strings of any CFG, we can predict that two CFG are equal or not.
❏ Ambiguity of CFG ?
There exist no algorithm which can check whether for the ambiguity of a CFL. We can only check if any particular string of the CFL generates two different parse trees then the CFL is ambiguous.
❏ Is it possible to convert a given ambiguous CFG into corresponding non-ambiguous CFL?
It is also an Undecidable Problem as there doesn’t exist any algorithm for the conversion of an ambiguous CFL to non-ambiguous CFL.
❏ Is a language Learning which is a CFL, regular ?
This is an Undecidable Problem as we can not find from the production rules of the CFL whether it is regular or not.
Q.9 ) Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
Have a Post Correspondence Solution?
Sol : It was introduced by Emil Post and is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x 1 , x 2 , x 3 ,………, x n )
N = (y 1 , y 2 , y 3 ,………, y n )
We can say that there is a Post Correspondence Solution, if for some i 1 ,i 2 ,………… i k ,
Where 1 ≤ i j ≤ n, the condition x i1 …….x ik = y i1 …….y ik satisfies.
According to given question, we make table -
| X1 | X2 | X3 |
M | Abb | Aa | Aaa |
N | Bba | Aaa | Aa |
Here,
x 2 x 1 x 3 = ‘aaabbaaa’
And y 2 y 1 y 3 = ‘aaabbaaa’
We can see that
x 2 x 1 x 3 = y 2 y 1 y 3
Hence, the solution is i = 2, j = 1, and k = 3.
Q.10 ) Explain the Rice’s theorem and discuss the decidable and undecidable issues ?
Sol : Rice’s Theorem -
Every non-trivial (answer isn’t known) downside on algorithmic numerable languages is undecidable.e.g.; If a language is algorithmic numerable, its complement are going to be algorithmic numerable or not is undecidable.
Reducibility and Undecidability
Language A is reducible to language B (represented as A≤B) if there exists a
Perform f which can convert strings in an exceedingly to strings in B as:
w ɛ A <=> f(w) ɛ B
Theorem 1: If A≤B and B is decidable then A is additionally decidable.
Theorem 2: If A≤B and A is undecidable then B is additionally undecidable.
➔ Decidable issues
A problem is decidable if we will construct a information processing system which
Can halt in finite quantity of your time for each input and provides answer as ‘yes’ or
‘no’. A decidable downside has associate degree formula to work out the solution for
a given input.
Examples
• Equivalence of 2 regular languages: Given 2 regular languages, there’s
Associate degree formula and information processing system to make a decision
Whether or not 2 regular languages are equal or not.
• Finiteness of normal language: Given an everyday language, there’s
Associate degree formula and information processing system to make a decision
Whether or not regular language is finite or not.
• Emptiness of context free language: Given a context free language, there’s
Associate degree formula whether or not CFL is empty or not.
➔ Undecidable issues
A problem is undecidable if there’s no information processing system which can
Continuously halt in a finite quantity of your time to provide an answer as ‘yes’ or ‘no’.
Associate degree undecidable downside has no formula to work out the solution for a
Given input.
Examples
• Ambiguity of context-free languages: Given a context-free language, there’s
No information processing system which can continuously halt in finite quantity of
Your time and provides answers whether or not language is ambiguous or not.
• Equivalence of 2 context-free languages: Given 2 context-free languages,
There’s no information processing system which can continuously halt in finite
Quantity of your time and provides answer whether or not 2 context free languages ar
Equal or not.
• Everything or completeness of CFG: Given a CFG and input alphabet,
Whether or not CFG can generate all doable strings of input alphabet (∑*)is
Undecidable.
• Regularity of CFL, CSL, REC and REC: Given a CFL, CSL, REC or REC,
Determinative whether or not this language is regular is undecidable.
Note: 2 in style undecidable issues ar halting downside of metal and angel dust (Post
Correspondence Problem). Semi-decidable issues
A semi-decidable downside is set of undecidable issues that information processing
System can continuously halt in finite quantity of your time for answer as ‘yes’ and
Will or might not halt for an answer as ‘no’.
Q.11) Write the different variants of Turing machine ?
Sol : Variants of Turing machine -
1. Multiple tracks Alan Turing Machine:
• A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
• A k-track information processing system may be simulated by one track
Information processing system.
2. Two-way infinite Tape Alan Turing Machine:
• Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
• Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
• It has multiple tapes and is controlled by one head.
• The Multi-tape information processing system is completely different from k-
Track information processing systems however communicative power is the same.
• Multi-tape information processing system may be simulated by single-tape
Information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
• The multi-tape information processing system has multiple tapes and multiple
Heads.
• Each tape controlled by separate head
• Multi-Tape Multi-head information processing system may be simulated by
Normal information processing system.
5. Multi-dimensional Tape Alan Turing Machine:
• It has multi-dimensional tape wherever head will move any direction that’s left,
Right, up or down.
• Multi-dimensional tape information processing system may be simulated by
One-dimensional information processing system.
6. Multi-head Alan Turing Machine:
• A multi-head information processing system contain 2 or additional heads to
Scan the symbols on constant tape.
• In one step all the heads sense the scanned symbols and move or write
Severally.
• Multi-head information processing system may be simulated by single head
Information processing system.
7. Non-deterministic Alan Turing Machine:
• A non-deterministic information processing system encompasses a single, a
Method infinite tape.
• For a given state and input image has at least one option to move (finite range
Of decisions for consecutive move), every selection many decisions of path that it’d
Follow for a given input string.
• A non-deterministic information processing system is adore settled
Information processing system.
Unit - 5
Turing Machines and Recursive Function Theory
Q.1 ) What is the linear bounded automata ?
Sol : Linear bounded Automata
A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.
A linear bounded automata can be defined in 8-tuple -
(Q, X, ∑, q0, ML, MR, δ, F)
Where
● Q is a finite set of states
● X is the tape alphabet
● ∑ is the input alphabet
● q0 is the initial state
● ML is the left end marker
● MR is the right end marker where MR ≠ ML
● δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.
● F is the set of final states.
Q.2 ) Explain the halting problem in turing machine ?
Sol : Halting problem
Input : A turing machine and an input string T.
Problem - Does the Turing machine complete the T-string computation in a finite number of steps? Either yes or no must be the answer.
Answer : We will first assume that there is such a Turing machine to solve this problem, and then we will demonstrate that it contradicts itself. This Turing machine would be called a Halting machine that produces in a finite amount of time a 'yes' or no'. The performance comes as 'yes' if the stopping machine finishes in a finite amount of time, otherwise as no'.
The following is a Halting Computer block diagram -
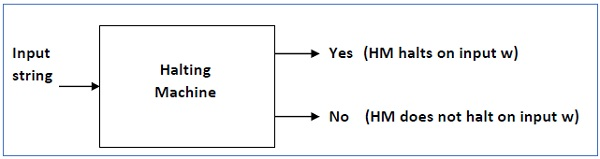
Now we will design an inverted halting machine (HM)’ as -
● If H returns YES, then loop forever.
● If H returns NO, then halt.
Below is the block diagram of inverted halting machine -
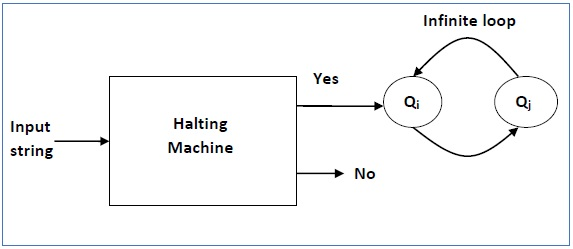
In addition, as follows, a machine (HM)2 whose input itself is constructed -
● If - (HM)2 halts on input, loop forever
● Else - halt
Now , we have a contradiction. So , the halting problem is undecidable .
Q.3 ) Describe the church’s thesis ?
Sol : Church’s thesis -
In 1936, a technique named as lambda-calculus was created by Alonzo Church
Within which the Church numerals area unit well outlined, i.e. the encryption of
Natural numbers. Additionally in 1936, mathematician machines (earlier known as
Theoretical model for machines) was created by mathematician, that’s used for
Manipulating the symbols of string with the assistance of tape.
Church mathematician Thesis :
Turing machine is outlined as associate degree abstract illustration of a computer
Like hardware in computers. Mathematician planned Logical Computing Machines
(LCMs), i.e. mathematician’s expressions for Turing Machines. This was done to
Outline algorithms properly. So, Church created a mechanical methodology named
As ‘M’ for manipulation of strings by mistreatment logic and arithmetic.
This methodology M should pass the subsequent statements:
• Number of directions in M should be finite.
• Output ought to be made when playing a finite variety of steps.
• It mustn’t be imagined, i.e. is created in the world.
• It mustn’t need any complicated understanding.
Using these statements Church planned a hypothesis known as Church’s
Mathematician thesis that may be expressed as: “The assumption that the intuitive
Notion of estimable functions is known with partial algorithmic functions.”
In 1930, this statement was initial developed by Alonzo Church and is typically
Brought up as Church’s thesis, or the Church-Turing thesis. However, this hypothesis
Can not be proved.
The algorithmic functions is estimable when taking following assumptions:
- Every and each operate should be estimable.
2. Let ‘F’ be the estimable operate and when playing some elementary operations to ‘F’, it'll rework a replacement operate ‘G’ then this operate ‘G’ mechanically becomes the estimable operate.
3. If any operates that follow on top of 2 assumptions should be states as an estimable function.
Q.4 ) What do you mean by modification of a Turing machine ?
Sol : A typical Turing Machine is a machine that moves either to the left or right when an input is given and it can overwrite the current symbol.
A Turing Machine can be described as a 7-tuple:
( Q, X , * , f, q0 , B, F )
Where,
Q - finite set of state
X - tape alphabet
* - input alphabet
f - transition function
f : Q x X - - > Q x X x { left_shift , right_shift }
q0 - initial state
B - blank symbol
F - set of final state
Some languages, called recursively enumerable languages, can be accepted by a regular Turing machine.
Let's see if we can increase the number of languages recognised by the Turing Machine by doing some form of modification.
- Turing machine with stay option
If the head could still remain in one position without moving anywhere instead of moving left or right on seeing an input, i.e.
f : Q x X - - > Q x X x { left_shift , right_shift }
The number of languages recognised by the Turing machine is still the same.
2. Turing machine with semi - infinite tape
We know that a turing machine has an infinite input tape with extends in both the direction (left or right). So now if we restrict it to extend only in one direction and not in both the directions, i.e. We make the tape semi-infinite, so the number of languages the Turing machine accepts remains the same as well.
3. Offline turing machine
Both the input and output are present on the tape in the traditional turing machine , the head has the power to travel over the input and can alter or change the input , if we don’t want to change the input we can have the input in a separate file, which is ready only then the head can’t make changes to it.
4. Jumping turing machine
The head of the regular Turing machine can move only one step to the right or left, but the head can move not only one step to the left or right if the Turing machine leaps, but it can move more than one step, i.e. 2, 3, 4, 5, 6,... Etc., or it can jump to any cell on the right or left of the input tape.
f : Q x X - - > Q x X x { left_shift , right_shift } x { n }
N is the number of moves we want to pass to the left or right. But the languages accepted by the Turing machine are still similar.
5. Non erasing turing machine
The input symbol can be converted to blank in the regular Turing machine, but if we eliminate this facility to change the input symbol to blank, this type of Turing machine is called a non-erasing Turing machine. We may substitute any other symbol other than blank for the input. The number of languages recognised by the Turing machine remains the same despite this update.
6. Always writing turing machine
Standard Turing machine gives us the power to leave it as it is without making any adjustments when seeing an input, but it is necessary to modify the input once we see it. We can not leave it as it is in always writing Turing machine. But this kind of change did not help to increase the number of languages that the Turing machine approved.
Therefore after making so many changes to the Turing machine, we see that the number of languages recognised by it is still the same. The Turing Machine is thus the most efficient machine.
Q.5 ) What kind of technique is used in a Turing machine construction ?
Sol : There are some technique for turing machine , which are -
● Storage in finite control
Technique: - Using the finite control of a TM to hold a finite amount of data, in addition to the state.
Method: - Assuming the state as [q, A, B, C], for example, when the finite control holds three data elements A, B, and C.
Example:
Design a TM to recognize 01* + 10*. The set of states are of the form [qi, X] where qi = q1, q2; X = 0, 1, B.
• The control portion (state) remembers what the TM is doing (q0 = not read 1st symbol; q1 = reverse).
• The data portion remembers the first symbol seen (0, or 1).
The transition function d is as follows.
• d([q0, B], a) = ([q1, a], a, R) for a = 0, 1. --- Copying the symbol it scanned.
• d([q1, a],a) = ([q1, a],a, R) wherea is the complement of a = 0, 1. --- Skipping symbols which are complements of the 1st symbol read (stored in the state as a).
• d([q1, a], B) = ([q1, B], B, R) for a = 0, 1. --- Entering the accepting state [q, B] when reaching the 1st blank.
● Multi tracks
➢ Assuming the tape of a TM as composed of several tracks.
➢ For example, if there are three tracks, we use the tape symbol as [X, Y, Z]
Example
The TM recognizes the non-CFL language
L = {wcw | w is in (0 + 1)+}.
Que: Why does not the power of the TM increase in this way?
Answer: just a kind of tape symbol labeling.
● Subroutine
Much as a computer programme has a primary procedure and procedure the TM can also be programmed to have subroutines, A core TM and TMs that function as subroutines.
Suppose we're going to make n copies of a word w Input is #w# and the output is #w# w| ww{z. . . w} n times .
In this situation, we can compose the mappings for a TM Msub That ends with #w#xw when launched on #w#x. This is called Msub x times by the key TM.
Likewise, for Multiplying two unary numbers m and n, on m occasions, n must be copied. For copying we can write a sub TM and main TM will name this m times.
The M1 and M2 states must be disjointed in order for a Turing machine M1 to use another Turing machine M2 as a subroutine. The control also goes to the initial state of M2 when M1 wishes to call M2, from the state of M1. When the subroutine stops and returns to M1, from M2's stopping state, the subroutine returns to M2 the computer goes into a certain M1 mode.
Notice that a subroutine TM calls its subroutine another TM (turing machine) This approach helps to construct a TM in a top-down way, separating the job into tasks and writing.
Q.6 ) Explain a Turing machine with some examples ?
Sol : Turing machine -
● A Turing Machine (TM) is a mathematical model which comprises an infinite length tape divided into cells on which input is given.
● It has a head which reads the input tape.
● A state register stores the current state.
● After an input symbol is read, it is replaced by another symbol, its internal state gets changed, and it moves from one cell to the right or left.
● After reaching the final state, the input string is accepted, otherwise rejected.
A TM can be formally described as a 7-tuple (Q, X, ∑, δ, q 0 , B, F)
Where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function; δ : Q × X → Q × X × {Left_shift, Right_shift}.
q 0 is the initial state
B is the blank symbol
F is the set of final states
Example
Turing machine M = (Q, X, ∑, δ, q 0 , B, F) with
Q = {q 0 , q 1 , q 2 , q f }
X = {a, b}
∑ = {1}
q 0 = {q 0 }
B = blank symbol
F = {q f }
δ is given by −
Tape alphabet symbol | Present state ‘q0’ | Present state ‘q1’ | Present state ‘q2’ |
a | 1Rq1 | 1Lq0 | 1Lqf |
b | 1Lq2 | 1Rq1 | 1Rqf |
Here 1Rq 1 write symbol is 1, the tape moves right, and the next state is q 1 . Similarly,
1Lq 2 write symbol is 1, the tape moves left, and the next state is q 2 .
Q.7 ) What do you mean by a Restricted turing machine ?
Sol : Restricted Turing Machine, included -
❖ TM with semi-infinite Tapes
Theorem -
Every language accepted by a TM M2 is also accepted by a TM M1 with the following restriction :
● M1’s head never moves left of it’s initial position
( so the tape is semi - infinite essential)
● M1 never writes a blank.
(M1 and M2 are equivalent .)
❖ Multistack Machine -
● Multistack Machine, which are restricted versions of TM , may be regarded as extension of pushdown automata (PDA’s)
● Actually , a PDA with two stacks has the same computation power as the TM .
● Theorem -
If a language is accepted by TM, then it is accepted by a two - stack machine .
❖ Counter Machine -
● There are two ways to think of a counter machine .
● First , As a multistack machine with each stack replaced by a counter regarded to be on a tape of a TM.
➔ A counter holds any non negative integer.
➔ The machine can only distinguish zero and non zero counters .
➔ The move conduct the following operation :
Changing the state ;
Add or subtract 1 from a counter which cannot become negative.
Q.8 ) What is the undecidable problem about turing machine , give some example also ?
Sol : Undecidable problem about turing machine
The problems for which we cannot make an algorithm that can answer the
Problems correctly in finite time are termed as Undecidable Problems.
- These problems may be partially decidable but they will never be decidable.
- Hence, there will always be a condition that leads the Turing Machine into an
Infinite loop without providing an answer at all.
- This can be explained by Fermat’s Theorem.
- A popular Undecidable Problem which states that no three positive integers a, b
And c for any n>2 can ever satisfy the equation: a^n + b^n = c^n.
- If we feed this problem to a Turing machine to find such a solution which gives a
Contradiction then a Turing Machine might run forever, to find the suitable values
Of n, a, b and c.
- But we are always unsure whether a contradiction exists or not and hence we
Term this problem as an Undecidable Problem.
Example -
These are few important Undecidable Problems:
❏ Whether a CFG generates all the strings or not?
As a CFG generates infinite strings, we can’t ever reach up to the last string and hence it is Undecidable.
❏ Whether two CFG L and M equal?
Since we cannot determine all the strings of any CFG, we can predict that two CFG are equal or not.
❏ Ambiguity of CFG ?
There exist no algorithm which can check whether for the ambiguity of a CFL. We can only check if any particular string of the CFL generates two different parse trees then the CFL is ambiguous.
❏ Is it possible to convert a given ambiguous CFG into corresponding non-ambiguous CFL?
It is also an Undecidable Problem as there doesn’t exist any algorithm for the conversion of an ambiguous CFL to non-ambiguous CFL.
❏ Is a language Learning which is a CFL, regular ?
This is an Undecidable Problem as we can not find from the production rules of the CFL whether it is regular or not.
Q.9 ) Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
Have a Post Correspondence Solution?
Sol : It was introduced by Emil Post and is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x 1 , x 2 , x 3 ,………, x n )
N = (y 1 , y 2 , y 3 ,………, y n )
We can say that there is a Post Correspondence Solution, if for some i 1 ,i 2 ,………… i k ,
Where 1 ≤ i j ≤ n, the condition x i1 …….x ik = y i1 …….y ik satisfies.
According to given question, we make table -
| X1 | X2 | X3 |
M | Abb | Aa | Aaa |
N | Bba | Aaa | Aa |
Here,
x 2 x 1 x 3 = ‘aaabbaaa’
And y 2 y 1 y 3 = ‘aaabbaaa’
We can see that
x 2 x 1 x 3 = y 2 y 1 y 3
Hence, the solution is i = 2, j = 1, and k = 3.
Q.10 ) Explain the Rice’s theorem and discuss the decidable and undecidable issues ?
Sol : Rice’s Theorem -
Every non-trivial (answer isn’t known) downside on algorithmic numerable languages is undecidable.e.g.; If a language is algorithmic numerable, its complement are going to be algorithmic numerable or not is undecidable.
Reducibility and Undecidability
Language A is reducible to language B (represented as A≤B) if there exists a
Perform f which can convert strings in an exceedingly to strings in B as:
w ɛ A <=> f(w) ɛ B
Theorem 1: If A≤B and B is decidable then A is additionally decidable.
Theorem 2: If A≤B and A is undecidable then B is additionally undecidable.
➔ Decidable issues
A problem is decidable if we will construct a information processing system which
Can halt in finite quantity of your time for each input and provides answer as ‘yes’ or
‘no’. A decidable downside has associate degree formula to work out the solution for
a given input.
Examples
• Equivalence of 2 regular languages: Given 2 regular languages, there’s
Associate degree formula and information processing system to make a decision
Whether or not 2 regular languages are equal or not.
• Finiteness of normal language: Given an everyday language, there’s
Associate degree formula and information processing system to make a decision
Whether or not regular language is finite or not.
• Emptiness of context free language: Given a context free language, there’s
Associate degree formula whether or not CFL is empty or not.
➔ Undecidable issues
A problem is undecidable if there’s no information processing system which can
Continuously halt in a finite quantity of your time to provide an answer as ‘yes’ or ‘no’.
Associate degree undecidable downside has no formula to work out the solution for a
Given input.
Examples
• Ambiguity of context-free languages: Given a context-free language, there’s
No information processing system which can continuously halt in finite quantity of
Your time and provides answers whether or not language is ambiguous or not.
• Equivalence of 2 context-free languages: Given 2 context-free languages,
There’s no information processing system which can continuously halt in finite
Quantity of your time and provides answer whether or not 2 context free languages ar
Equal or not.
• Everything or completeness of CFG: Given a CFG and input alphabet,
Whether or not CFG can generate all doable strings of input alphabet (∑*)is
Undecidable.
• Regularity of CFL, CSL, REC and REC: Given a CFL, CSL, REC or REC,
Determinative whether or not this language is regular is undecidable.
Note: 2 in style undecidable issues ar halting downside of metal and angel dust (Post
Correspondence Problem). Semi-decidable issues
A semi-decidable downside is set of undecidable issues that information processing
System can continuously halt in finite quantity of your time for answer as ‘yes’ and
Will or might not halt for an answer as ‘no’.
Q.11) Write the different variants of Turing machine ?
Sol : Variants of Turing machine -
1. Multiple tracks Alan Turing Machine:
• A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
• A k-track information processing system may be simulated by one track
Information processing system.
2. Two-way infinite Tape Alan Turing Machine:
• Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
• Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
• It has multiple tapes and is controlled by one head.
• The Multi-tape information processing system is completely different from k-
Track information processing systems however communicative power is the same.
• Multi-tape information processing system may be simulated by single-tape
Information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
• The multi-tape information processing system has multiple tapes and multiple
Heads.
• Each tape controlled by separate head
• Multi-Tape Multi-head information processing system may be simulated by
Normal information processing system.
5. Multi-dimensional Tape Alan Turing Machine:
• It has multi-dimensional tape wherever head will move any direction that’s left,
Right, up or down.
• Multi-dimensional tape information processing system may be simulated by
One-dimensional information processing system.
6. Multi-head Alan Turing Machine:
• A multi-head information processing system contain 2 or additional heads to
Scan the symbols on constant tape.
• In one step all the heads sense the scanned symbols and move or write
Severally.
• Multi-head information processing system may be simulated by single head
Information processing system.
7. Non-deterministic Alan Turing Machine:
• A non-deterministic information processing system encompasses a single, a
Method infinite tape.
• For a given state and input image has at least one option to move (finite range
Of decisions for consecutive move), every selection many decisions of path that it’d
Follow for a given input string.
• A non-deterministic information processing system is adore settled
Information processing system.