Unit 2 | unit 2 basic parsing techniques

Unit - 2

Basic Parsing Techniques

Q1) Define top-down parsing with its types?

A1) Top-down parsing

Recursive or predictive parsing is known as top-down parsing.

The parsing begins with the start symbol in the top-down parsing and transforms it into the input symbol.

The top-down parser is the parser that, by expanding the non-terminals, generates a parse for the given input string with the aid of grammar productions, i.e., it begins from the start symbol and ends on the terminals.

Parse Tree The input string representation of acdb is as follows:

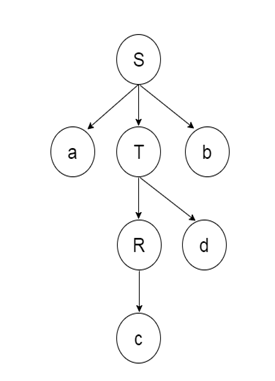
There are 2 types of additional Top-down parsers: Recursive descent parser, and Non-recursive descent parser.

Recursive descent parser:

It is also known as Brute force parser or the backtracking parser. Basically, by using brute force and backtracking, it produces the parse tree.

A top-down parsing technique that builds the parse tree from the top and reads the input from left to right is recursive descent. For any terminal and non-terminal entity, it uses procedures.

The input is recursively parsed by this parsing technique to make a parse tree, which may or may not require back-tracking. But the related grammar (if not left-faced) does not prevent back-tracking. Predictive is considered a type of recursive-descent parsing that does not require any back-tracking.

As it uses context-free grammar that is recursive, this parsing technique is called recursive.

II. Non-recursive descent parser:

It is also known with or without a backtracking parser or dynamic parser, LL (1) parser, or predictive parser. It uses the parsing table instead of backtracking to create the parsing tree.

Q2) Define parsers and their types?

A2) Parser

The parser is a compiler used to break down the information from the lexical analysis process into smaller components.

A parser receives input in the form of a token sequence and generates output in the form of a parse tree.

The parser is the compiler level, which uses a token string as input and transforms it into the corresponding parse tree with the aid of existing grammar. Often known as Syntax Analyzer.

Parsing consists of two types: parsing top-down and parsing bottom up.

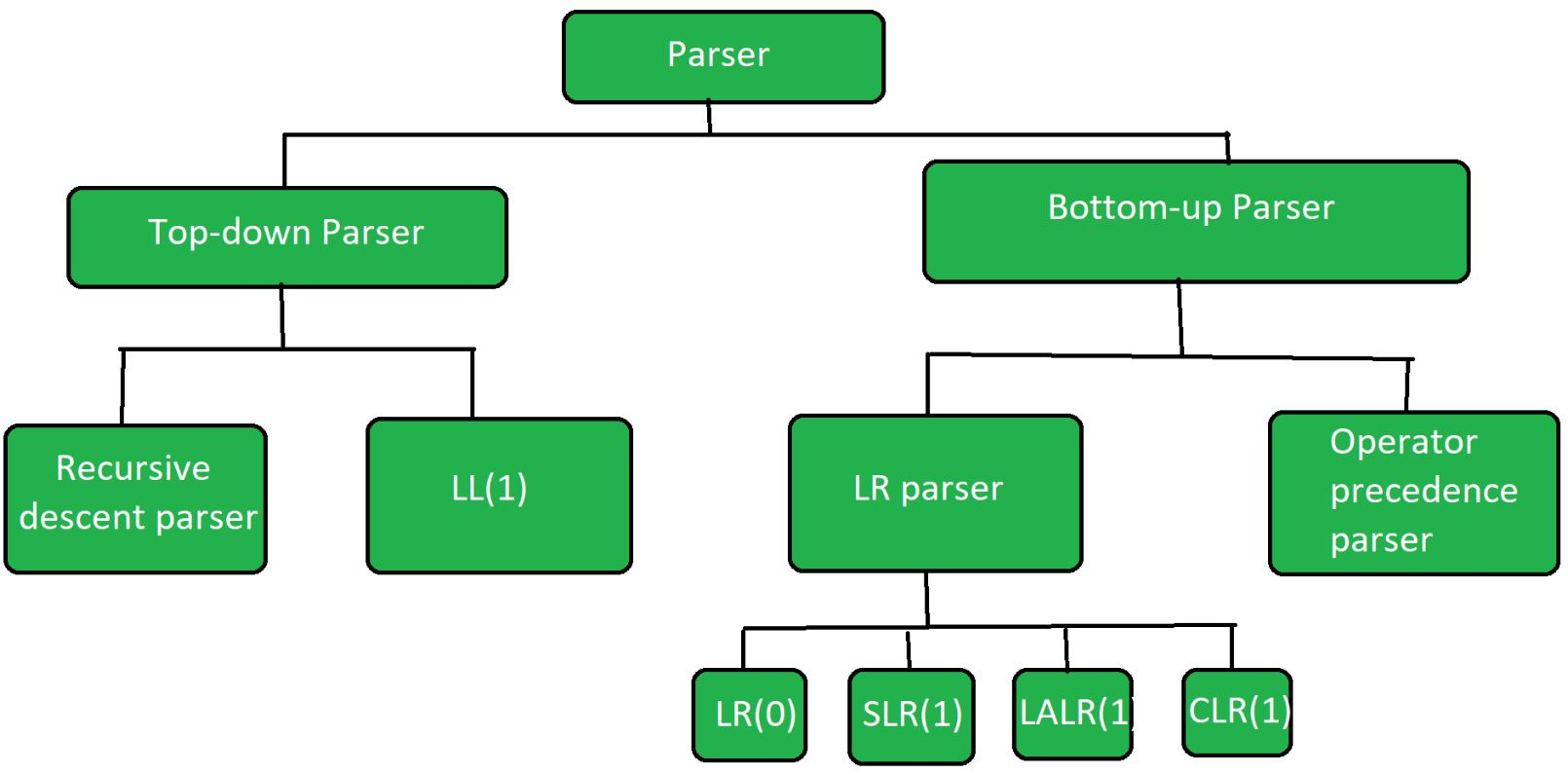
Q3) Define bottom-up praising and its types?

A3) Bottom-up parsing

Bottom-up parsing is also known as parsing for shift-reduce.

Bottom-up parsing is used to build an input string parsing tree.

The parsing begins with the input symbol in the bottom-up parsing and builds the parse tree up to the start symbol by tracing the rightmost string derivations in reverse.

Parsing from the bottom up is known as multiple parsing. Those are like the following:

Shift-Reduce Parsing

Operator Precedence Parsing

Table Driven LR Parsing

LR (1)

SLR (1)

CLR (1)

LALR (1)

Q4) What do you mean by Shift-Reduce Parsing and its types? Describe with example?

A4) Shift reduce parsing

● Shift reduction parsing is a mechanism by which a string is reduced to the beginning symbol of a grammar.

● Using a stack to hold the grammar and an input tape to hold the string, Shift reduces parsing.

● The two acts are done by Sift Decrease Parsing: move and decrease. This is why it is considered that shift-reduce parsing.

● The current symbol in the input string is moved into the stack for the shift operation.

● The symbols will be substituted by the non-terminals at each reduction. The mark is the right side of manufacturing and the left side of output is non-terminal.

Example:

Grammar:

S → S+S

S → S-S

S → (S)

S → a

Input string:

a1-(a2+a3)

Parsing table:

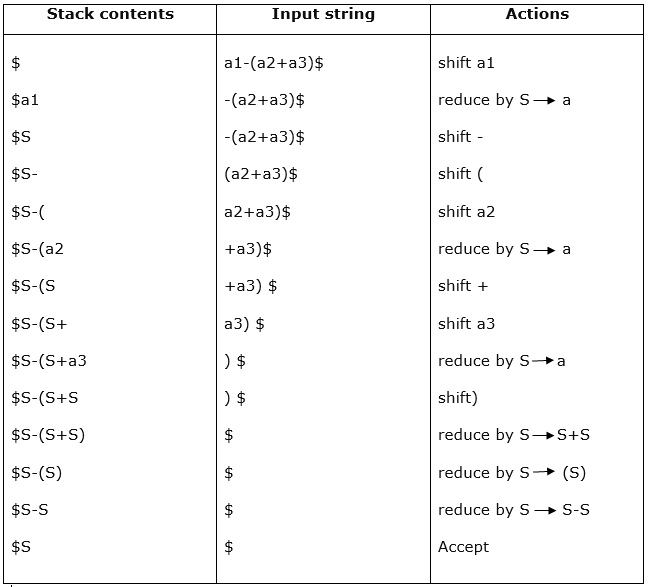
For bottom-up parsing, shift-reduce parsing uses two special steps. Such steps are referred to as shift-step and reduce-step.

Shift - step: The shift step refers to the progression to the next input symbol, which is called the shifted symbol, of the input pointer. Into the stack, this symbol is moved. The shifted symbol will be viewed as a single parse tree node.

Reduce - step: When a complete grammar rule (RHS) is found by the parser and substituted with (LHS), it is known as a reduction stage. This happens when a handle is located at the top of the stack. A POP function is performed on the stack that pops off the handle and substitutes it with a non-terminal LHS symbol to decrease.

As follows, there are two major types of shift reduction parsing:

Operator-Precedence Parsing

LR-Parser

Q5) What is LR-Parser?

A5) LR parsers

● In the LR parser, “L” means left to right scanning of any input.

● One form of bottom-up parsing is LR parsing. It is used to evaluate a broad grammar class.

● R" stands for the construction of a proper reverse derivation.

● "K" is the number of look-ahead input symbols used to make some parsing decisions.

LR parsing is divided into four parts: parsing for LR (0), parsing for SLR, parsing for CLR, and parsing for LALR.

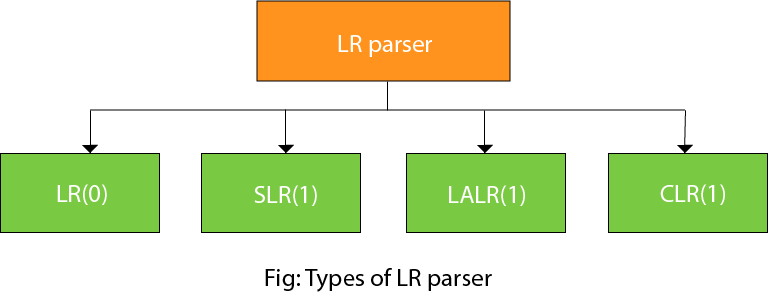
LR algorithm:

The stack, input, output, and parsing table are required by the LR algorithm. The input, output, and stack are the same in all modes of LR parsing, but the parsing table is different.

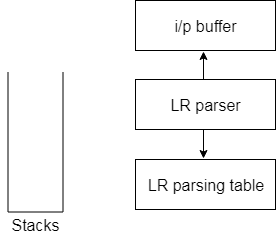
● The input buffer is used to denote the end of the input and includes the string followed by the $ symbol to be parsed.

● To contain a series of grammar symbols with $ at the bottom of the stack, a stack is used.

● A two-dimensional array is a parsing table. It comprises two parts: The action part and Goes To part.

LR (1) parser:

Different steps involved in LR (1) Parsing:

❏ Write context-free grammar for the specified input string.

❏ Verify the grammar's uncertainty.

❏ Add the Augmentation output to the specified grammar.

❏ Creating a canonical set of objects from LR (0).

❏ Drawing a diagram of data flow (DFA).

❏ Build a table for LR (1) parsing.

Augment Grammar:

If we add one more output to the given grammar G, Augmented Grammar G will be generated. It allows the parser to define when the parsing should be stopped and to announce the acceptance of the input.

Example

Given grammar

S → AA

A → aA | b

The Augment grammar G is represented by

S→ S

S → AA

A → aA | b

Q6) How to construct an LALR parsing table?

A6) LALR parsing tables

The lookahead LR is alluded to by LALR. We use the canonical set of LR (1) objects to create the LALR (1) parsing table.

In the LALR (1) analysis, the LR (1) products that have the same outputs but look ahead differently are combined to form a single set of items

The parsing of LALR (1) is the same as the parsing of CLR (1), the only distinction in the parsing table.

LALR (1) Parsing:

LALR refers to the lookahead LR. To construct the LALR (1) parsing table, we use the canonical collection of LR (1) items.

In the LALR (1) parsing, the LR (1) items that have the same productions but different look ahead is combined to form a single set of items

LALR (1) parsing is the same as the CLR (1) parsing, with only a difference in the parsing table.

Example

LALR (1) Grammar

S → AA

A → aA

A → b

Add Augment Production, insert the '•' symbol for each production in G at the first place, and add the look ahead as well.

S → •S, $

S → •AA, $

A → •aA, a/b

A → •b, a/b

I0 State:

Add the output of Augment to the I0 State and measure Closure L

I0 = Closure (S → •S)

Add all productions beginning with S to I0 State, since the non-terminal is followed by '•'. The I0 Condition, then, becomes

I0 = S → •S, $

S → •AA, $

In changed I0 State, add all productions beginning with A since "•" is followed by the non-terminal. So, it will become the I0 State.

I0= S → •S, $

S → •AA, $

A → •aA, a/b

A → •b, a/b

I1= Go to (I0, S) = closure (S → S•, $) = S → S•, $

I2= Go to (I0, A) = closure (S → A•A, $)

In the I2 State, add all productions beginning with A since "•" is followed by the non-terminal. The I2 Condition, then, becomes

I2= S → A•A, $

A → •aA, $

A → •b, $

I3= Go to (I0, a) = Closure (A → a•A, a/b)

In the I3 State, add all productions beginning with A since "•" is followed by the non-terminal. The I3 Condition, then, becomes

I3= A → a•A, a/b

A → •aA, a/b

A → •b, a/b

Go to (I3, a) = Closure (A → a•A, a/b) = (same as I3)

Go to (I3, b) = Closure (A → b•, a/b) = (same as I4)

I4= Go to (I0, b) = closure (A → b•, a/b) = A → b•, a/b

I5= Go to (I2, A) = Closure (S → AA•, $) =S → AA•, $

I6= Go to (I2, a) = Closure (A → a•A, $)

"In I6 State, add all productions beginning with A since "•" is followed by the non-terminal. The I6 Condition, then, becomes

I6 = A → a•A, $

A → •aA, $

A → •b, $

Go to (I6, a) = Closure (A → a•A, $) = (same as I6)

Go to (I6, b) = Closure (A → b•, $) = (same as I7)

I7= Go to (I2, b) = Closure (A → b•, $) = A → b•, $

I8= Go to (I3, A) = Closure (A → aA•, a/b) = A → aA•, a/b

I9= Go to (I6, A) = Closure (A → aA•, $) A → aA•, $

If we evaluate, then I3 and I6 things from LR (0) are the same, but they only differ in their lookahead.

I3 = {A → a•A, a/b

A → •aA, a/b

A → •b, a/b

}

I6= {A → a•A, $

A → •aA, $

A → •b, $

}

In their LR (0) objects, I3 and I6 are obviously the same but differ in their lookahead, so we can combine them and name them I36.

I36 = {A → a•A, a/b/$

A → •aA, a/b/$

A → •b, a/b/$

}

The I4 and I7 are the same but they vary only in their look ahead, so we can combine them and called I47.

I47 = {A → b•, a/b/$}

The I8 and I9 are the same, but they just vary in their outlook, so we can merge them and name them I89.

I89 = {A → aA•, a/b/$}

Drawing DFA: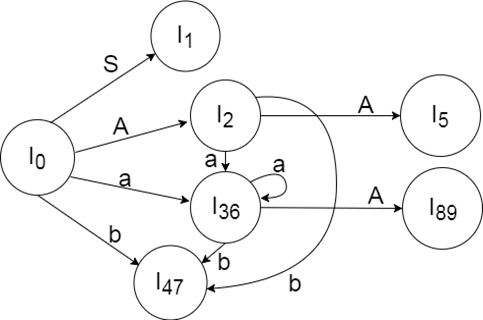

LALR (1) Parsing Table: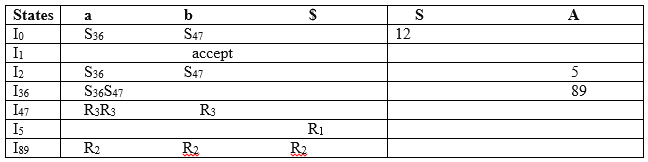

Q7) Describe the implementation of LR parsing tables?

A7) implementation of LR parsing tables

During the syntax review, we will consider the problem of how to select the products to be used. To this end, for a given grammar G, we use a predictive parsing table.

We use the following algorithm whose key ideas are used to construct this table:

1. Suppose that A → α is output with an in FIRST(α). Then, when the current input symbol is the parser extends A by α.

2. Complication happens when α = ∈ or α ∗⇒ ∈. In this scenario, again, we need to be If the current input symbol is in FOLLOW (A), extend A by α

Algorithm:

Input: Grammar G

Output: Parsing table M

Algorithm: Construction of a predictive parsing table

1. For each production A → α of G, do steps 2 and 3

2. For each terminal an in FIRST(α), add A → α to M [A, a]

3. If α ∗⇒ ∈, add A → α to M [A, b] for each terminal b in FOLLOW(A)

If α ∗⇒∈ and $ is in FOLLOW(A), add A → α to M [A, $]

4. Make each undefined entry of M be error

Example:

Grammar G 3 = ({E, E′, T, T ′, F}, {a, ∗, +, (,)}, P, E) with the set of productions P:

E → TE′ T → FT ′

F → (E) E′ → +TE′

T ′ → ∗FT ′ F → a

E′ → ∈ T ′ → ∈

Parsing table M:

Q8) what is recursive descent parser?

A8) Recursive descent parser:

It is also known as the Brute force parser or the backtracking parser. Basically, by using brute force and backtracking, it produces the parse tree.

A top-down parsing technique that builds the parse tree from the top and reads the input from left to right is recursive descent. For any terminal and non-terminal entity, it uses procedures.

As it uses context-free grammar that is recursive, this parsing technique is called recursive.

Q9) Describe parsing action with example?

A9) Parsing Action

➔ Add the $ symbol at both ends of the specified input string.

➔ Now search the right-left input string until the ⁇ is encountered.

➔ Scan to the leftover all of the equal precedence’s until much of the first left is met.

➔ A handle is anything between most of the left and most of the right.

➔ $ on $ means the parsing succeeds.

Example - Grammar:

E → E+T/T

T → T*F/F

F → id

Given string:

w = id + id * id

For it, let us take a parse tree as follows:

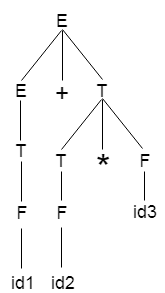
We can design the following operator precedence table based on the tree above:

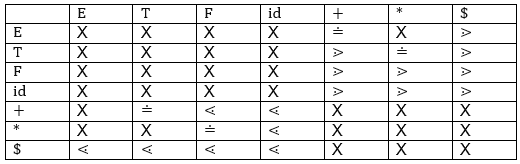
Let us now process the string with the assistance of the precedence table above:

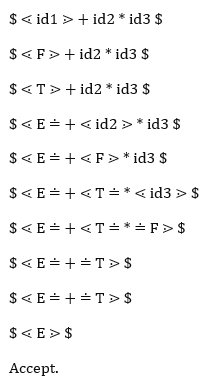
Q10) Define LR Algorithm?

A10) LR algorithm:

The stack, input, output, and parsing table are required by the LR algorithm. The input, output, and stack are the same in all modes of LR parsing, but the parsing table is different.

● The input buffer is used to denote the end of the input and includes the string followed by the $ symbol to be parsed.

● To contain a series of grammar symbols with $ at the bottom of the stack, a stack is used.

● A two-dimensional array is a parsing table. It comprises two parts: The action part and the Goes To part.

LR (1) parser:

Different steps involved in LR (1) Parsing:

❏ Write context-free grammar for the specified input string.

❏ Verify the grammar's uncertainty.

❏ Add the Augmentation output to the specified grammar.

❏ Creating a canonical set of objects from LR (0).

❏ Drawing a diagram of data flow (DFA).

❏ Build a table for LR (1) parsing.

Augment Grammar:

If we add one more output to the given grammar G, Augmented Grammar G will be generated. It allows the parser to define when the parsing should be stopped and to announce the acceptance of the input.

Example

Given grammar

S → AA

A → aA | b

The Augment grammar G is represented by

S→ S

S → AA

A → aA | b

Sign Up