Unit - 5

Code Generation

Q1) What is the target language?

A1) Target language

For designing a successful code generator, familiarity with the target computer and its instruction set is a prerequisite. Unfortunately, it is not possible to explain any target machine in enough detail in a general discussion of code generation to produce good code for a complete language on that machine.

For a simple computer that is representative of many register machines, we will use assembly code as a target language.

A Simple Target Machine Model

A three-address machine with load and store operations, computing operations, jump operations, and conditional jumps is modeled on our target computer. A byte-addressable machine with n general-purpose registers is the underlying computer, R0, R1,..., Rn —1. There will be dozens of instructions for a fully-fledged assembly language. We will use a very minimal set of instructions to avoid hiding the concepts in a plethora of specifics and presume that all operands are integers.

Many instructions consist of an operator, followed by a target, followed by a list of operands from the source. An instruction can precede a mark. We presume there are the following kinds of instructions:

●      Load operations: The LD dst, addr command loads the value from the addr location to the dst location. This command signifies the dst=addr assignment. LD r, x, which loads the value at position x into register r, is the most common type of this instruction. The LD r±, r2 type instruction is a register-to-register copy in which the contents of the r2 register are copied to the r1 register.

●      Store operations: In the ST x, r command, the value in register r is stored at position x. The assignment x = r is denoted by this instruction.

●      OP dst, src1, src2 type computation operations, where OP is an operator, such as ADD or SUB, and dst, srcy, and src2 are positions, not necessarily different. The application of the operation is the result of this computer instruction.

●      Unconditional jumps: The BR L instruction allows power to branch to the label L computer instruction. (BR means branch.)

●      Conditional jumps of the form Bcond r, L, where r is a register, L is a label, and cond is one of the common checks in the register r for values.

Program and Instruction Costs

We also equate a price with the compilation and execution of a programme. Depending on what aspect of a programme we are interested in optimizing, the length of compilation time and the scale, running time, and power consumption of the target programme are some typical cost measures.

A complex problem is calculating the actual cost of compiling and running a programme.

It is an undecidable problem in general to find an optimal target programme for a given source programme, and many of the sub-problems involved are NP-hard.

 As we have shown, we must sometimes be satisfied with heuristic techniques in code generation that generate successful but not necessarily optimal target programmes.

We take the cost of an instruction to be one for simplicity plus the costs associated with the operand addressing modes. This cost relates to the duration of the instruction in words. There are zero additional costs for addressing modes involving registers, while those involving a memory location or constant in them have an additional cost of one since such operands must be stored in the words following the instruction.

Example:

 Move register to memory R0 → M

MOV R0, M 

cost = 1+1+1 (Since the memory location address M is in the word following the instruction)

Q2) What is the basic graph?

A2) Basic graph

The Basic Block includes a declaration sequence. The control flow enters at the beginning of the sentence and leaves without any halt at the end (except maybe the last instruction of the block).

A fundamental block is generated by the following sequence of three address statements:

Basic block construction:

Algorithm: Partition into basic blocks

Input: It comprises the series of three sentences of address

Output: It comprises a list of basic blocks in exactly one block with three address statements each.

Method: Identify the leader in the code first. The guidelines are as follows for finding leaders:

●      Instruction L is a leader if a goto or conditional goto sentence like if goto B or goto B is followed immediately.

The basic block for each leader consists of the leader and all statements up to that. The next leader and the end of the curriculum are not included.

For the dot product of two vectors a and b of length 10, consider the following source code:

begin  

           prod:=0;  

i:=1;  

do begin  

prod:=prod+ a[i] * b[i];  

i:=i+1;  

end  

while i <= 10  

end 

The three address codes for the source programme above are given below:

B1

B2

The basic block B1 contains the declaration (1) to (2)

The basic block B2 contains a declaration (3) to (12)

Q3) Define a flow graph?

A3) Flowgraph

A directional graph is a flow graph. It contains the control information stream for the basic block collection.

A control flow graph is used to show how the control of the programme between the blocks is parsed. It is helpful in the optimization of the loop.

The vector dot product's flow graph is given as follows:

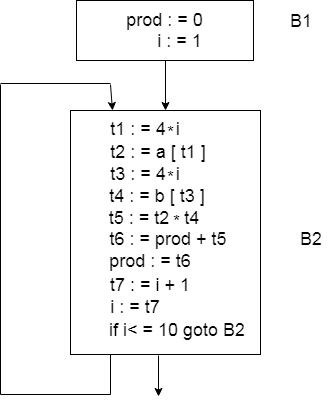
●      The initial node is block B1. Block B2 follows B1 immediately, so an edge occurs from B2 to B1.

●      The jump goal from the last statement of B1 is the first statement of B2, so there is an edge from B1 to B2.

●      B2 is a successor to B1 and the precursor to B2 is B1

Q4) What do you mean by machine-independent optimization?

A4) Machine - independent optimization

❖      To get a better target code, computer independent optimization attempts to enhance the intermediate code. No absolute memory location or any CPU registers are involved in the portion of the code that is transformed here.

❖      Much inefficiency is introduced by the intermediate code generation method such as: using variables instead of constants, additional copies of variable, repetitive expression evaluation. You can eliminate certain efficiencies and optimize code through the optimization of code.

❖      Often it can modify the programme structure beyond recognition, such as unrolling loops, inline functions, removing certain programmer-defined variables.

Code Optimization can be carried out in the following ways:

1) Compile Time Evaluation:

(a) a = 5*(45.0/5.0) *r

  Perform 5*(45.0/5.0) *r at compile time.

(b) s = 5.7

  t = s/3.6

 Evaluate s/3.6 as 5.7/3.6 at compile time.

2) variable propagation:

The code before optimization is:

y = w * x                                              

a = w                                                 

till                                                           

z = a * x + 4  

The code after optimization is:

y = w * x  

a = aw

till 

 z = w * x + 4 

Here, w * x and a * x are defined as a typical sub-expression after variable propagation.

3) Dead code elimination:

The code before elimination:

c = a * b                                                 

x = b                                                

till                                                         

d = a * b + 4   

The code after elimination:

c = a * b 

till 

d = a * b + 4 

Here, x= b is a dead state, since it can never be included in the software afterwards. So, we can get this state removed.

4) Code motion:

●      It reduces the evaluation frequency of expression.

●      It brings loop invariant statements out of the loop.

do 

{ 

   item = 10; 

   valuevalue = value + item;  

} while(value<100); 

//This code can be further optimized as   

item = 10; 

do 

{ 

   valuevalue = value + item;  

} while(value<100);

5) Induction variable and strength reduction:

●      Strength reduction is used to replace the high strength operator with low strength.

●      An induction variable is used in the loop for the following kind of assignment like I = I + constant.

Before reduction the code is:

i = 1;                                                   

while(i<10)                                               

{                                                       

    y = i * 4;  

} 

After Reduction the code is:

i = 1 

t = 4 

{  

   while( t<40)  

  y = t;  

  t = t + 4; 

} 

Q5) Describe loop optimization?

A5) Loop optimization

Loop optimization is the most useful machine-independent optimization since the inner loop of the software requires a programmer's time in bulk.

When we reduce the number of instructions in an inner loop, even though we increase the amount of code outside that loop, the running time of a programme can be increased.

The following three techniques are critical for loop optimization:

To minimize the amount of code in the loop, code movement is used. This transition involves a statement or expression that can be transferred beyond the body of the loop without affecting the program's semantics.

Example:

The limit-2 equation is a loop invariant equation in the sense argument.

while (i<=limit-2)     /*statement does not change limit*/ 

After code motion the result is as follows: 

          a= limit-2; 

          while(i<=a) /*statement does not change limit or a*/ 

2. Induction-variable elimination

To substitute the variable from the inner loop, induction variable removal is used.

In a loop, it may reduce the number of additions. It enhances the efficiency of both code space and runs time.

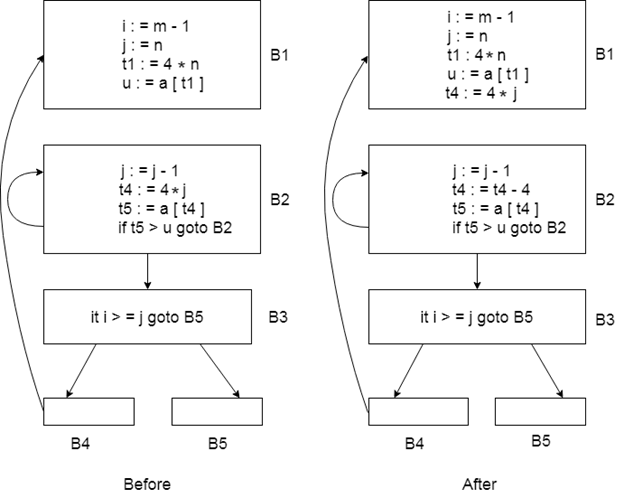
We can replace the assignment t4: =4*j in this figure with t4: =t4-4. The only issue that will occur is that when we first join block B2, t4 does not have a meaning. So, we put a t4=4*j relationship on the B2 block entry.

3. Strength reduction

Example:

while (i<10) 

        { 

j= 3 * i+1; 

a[j]=a[j]-2; 

i=i+2; 

        } 

The code would be, after strength reduction:

s= 3*i+1; 

      while (i<10) 

       { 

            j=s; 

            a[j]= a[j]-2; 

            i=i+2; 

            s=s+6; 

       } 

It is easier to compute s=s+6 in the above code than j=3 *i

Q6) Describe Global data flow analysis?

A6) Global Data-Flow analysis

❏      The code compiler gathers all the programme information and distributes this information to each block of the flow graph to efficiently optimize it. This method is known as the study of data-flow graphs.

❏      Only by analyzing the entire programme can such optimization be achieved. It can't be done by only reviewing a portion of the curriculum.

❏      One unique issue is user-defined chaining for this form of optimization.

❏      Using the variable value here, we try to figure out what meaning of a variable in a sentence is applicable.

A compiler can perform such optimizations based on the local data. Consider, for instance, the following code:

x = a + b; 

x = 6 * 3 

●      The first assignment of x in this code is useless. In the programme, the value machine for x is never used.

●      The expression 6*3 will be computed at compile-time, simplifying the second assignment statement to x = 18;

More global knowledge requires some optimization. Consider, for instance, the following code:

a = 1; 

   b = 2; 

   c = 3; 

   if (....) x = a + 5; 

   else x = b + 4; 

   c = x + 1; 

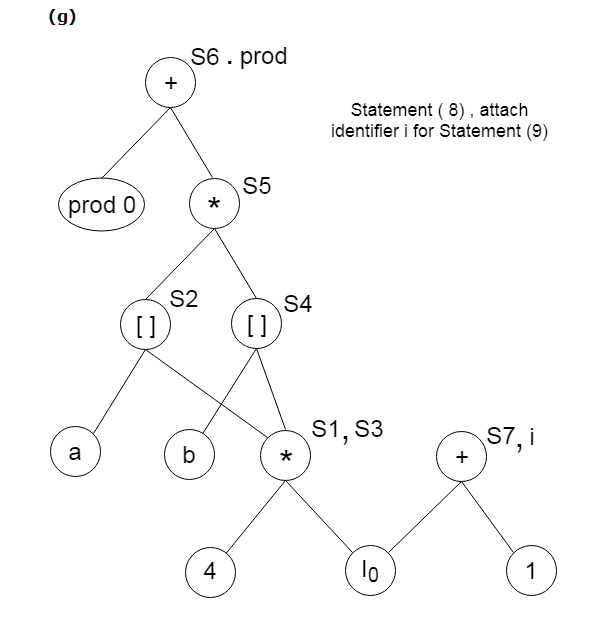
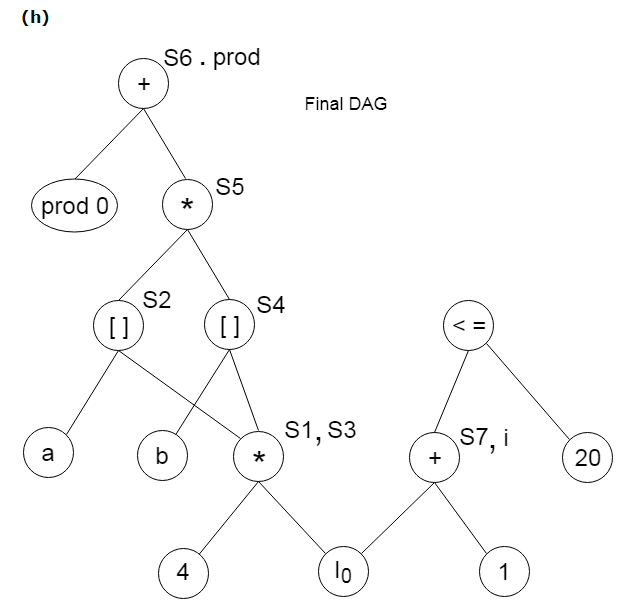
Q7) Describe stages in DAG Construction?

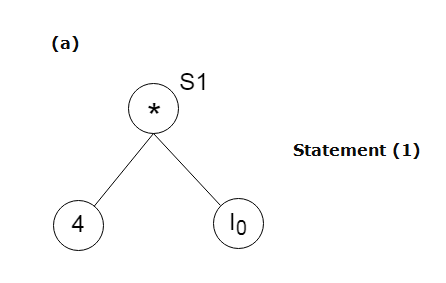
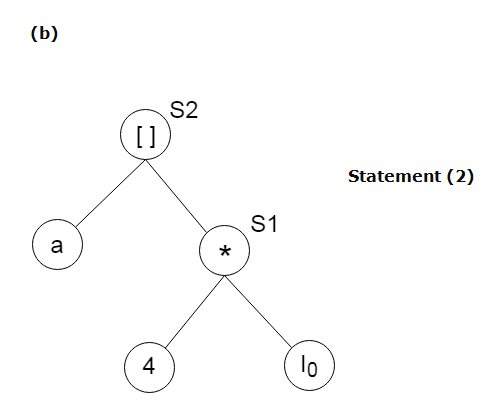
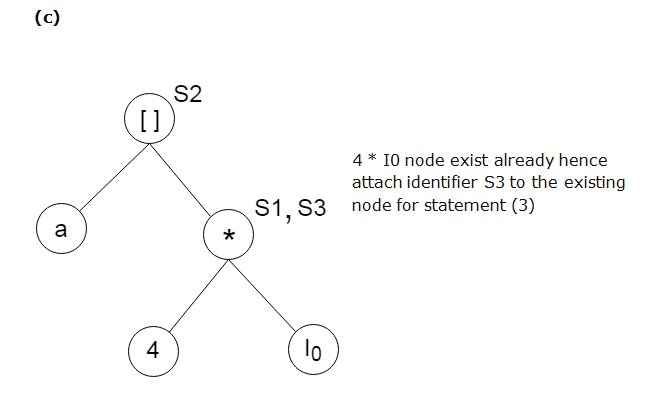
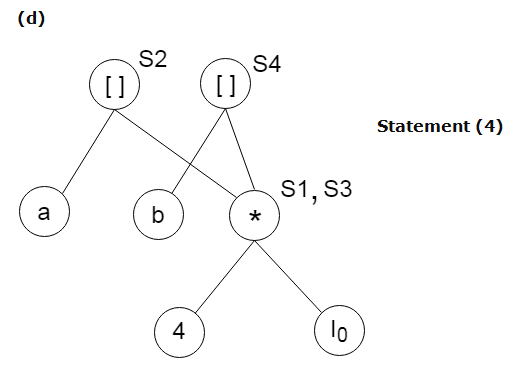
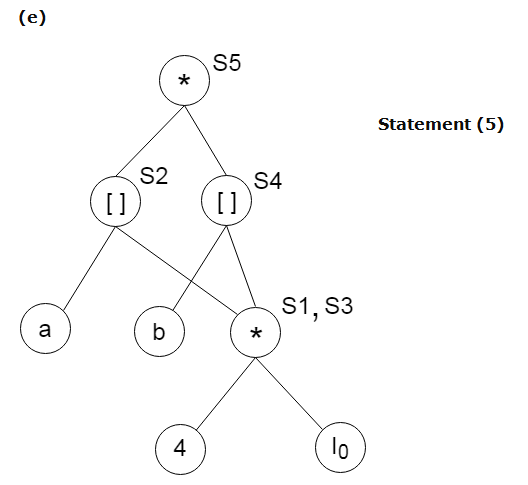
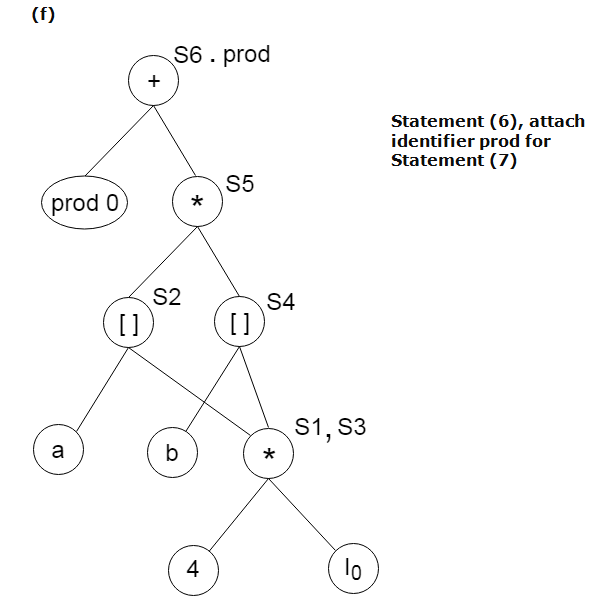
Find the following three statements of address:

S1: = 4 * i 

S2: = a[S1] 

S3: = 4 * i 

S4: = b[S3]   

S5: = s2 * S4 

S6: = prod + S5 

Prod: = s6 

S7: = i+1 

i: = S7 

if i<= 20 goto (1)

A7) Stages in DAG Construction:

Q8) Illustrate value numbers and algebraic laws?

A8) value numbers and algebraic laws

Value numbering is a method of deciding whether two computations are identical in a programme and replacing one of them with an optimization preserving semantics.

Global value numbering

Global value numbering (GVN) is a compiler optimization focused on the intermediate representation of the static single assignment type (SSA). It also helps remove redundant code that does not eliminate common subexpression (CSE). However, at the same time, CSE can delete code that GVN doesn't do, so both are often found in modern compilers.

By assigning a value number to variables and expressions, global value numbering works. For those variables and expressions which are known to be equal, the same value number is assigned. In the following code, for instance:

w: = 3

x: = 3

y: = x + 4

z: = w + 4

A successful GVN routine will assign w and x to the same number of values, and y and z to the same number of values. For example, for this block, the 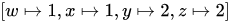map would be an optimal number-value mapping. Using this information, you can safely turn the previous code fragment into:

w: = 3

x: = w

y: = w + 4

z: = y

Local value numbering

Local value numbering (LVN) is an optimization of the compiler that seeks to find and replace several instances of identical expressions (i.e., expressions that yield the same result) with the first occurrence. LVN is a local optimization, which means it works on a single simple block at a time, unlike global value numbering.

a ← 4         a is tagged as #1

b ← 5         b is tagged as #2

c ← a + b     c (#1 + #2) is tagged as #3

d ← 5         d is tagged as #2, the same as b

e ← a + d     e, being '#1 + #2' is tagged as #3

Algebraic

Algebraic identities represent another important class of optimizations on basic blocks. For example, we may apply arithmetic identities, such as

x + 0 = 0 + x = x x - 0 = x

Q9) What do you mean by optimization of basic blocks?

A9) Optimization of Basic Blocks

The process of optimization can be extended to a simple block. We don't need to adjust the set of expressions computed by the block during optimization.

There are two forms of simple optimization for blocks. Those are like the following:

The main Structure-Preserving Basic Block Transformation is as follows:

You do not need to be computed again and again in the common sub-expression. Instead, you can compute it once and store it from where it is referenced when it is again encountered.

a: = b + c 

b: = a - d  

c: = b + c                         

d: = a - d

In the expression above, the same expression was computed in the second and fourth expressions. So, it is possible to transform the block as follows:

a: = b + c  

b: = a - d                                                        

c: = b + c 

d: = b

D. Interchange of two independent adjacent statement

Suppose the following two adjacent statements are given to a block:

t1: = b + c  

t2: = x + y 

If the value of t1 does not affect the value of t2, these two statements can be interchanged without affecting the value of the block.

a: = b + c 

e: = c +d +b 

They will generate the following intermediate code:

a: = b + c 

 t: = c +d 

 e: = t + b

Q10) Describe the code generator?

A10) Code Generator

For three-address statements, the code generator is used to generate the target code. It uses registers to store the three address statement operands.

Consider the three address statements a = b + c. The following sequence of codes may be available.

MOV a, R0

ADD b, R0

Register and Address Descriptors:

➢      The track of what is currently in each register is contained in a register descriptor. The register descriptors mean that all the registers are initially empty.

➢      An address descriptor is used to store the location where you can find the name's current value at runtime.

A code - generation algorithm:

A set of three-address statements is taken as input by the algorithm. The various acts are performed for every three address statements of the form a: = b op c. Those are like the following:

➢      Invoke a getreg function to find out where the output of the b op c calculation should be stored at position L.

➢      If the value of y is already in memory and register both then prefer the register y ‘. If the value of y is not already in L, then generate the instruction MOV y', L to put a copy of y in L. If the value of y is not already in L, then generate the instruction MOV y', L.

➢      Generate the OP z', L instruction where z 'is used to represent z's current position. If z is in both, then a memory location is preferred to a register.

Update the x address descriptor to specify that x is located at position L. If x is in L, then the descriptor is modified and x is omitted from all other descriptors.

➢      If the current value of y or z is not used or lives on exit from the block or in the register, change the register descriptor to show that such registers will no longer contain y or z after the execution of x: =y op z.

Generating Code for Assignment Statements:

The d: = (a-b) + (a-c) + (a-c) assignment statement can be translated into the following sequence of three address codes:

t: = a-b 

 u: = a-c 

 v: = t +u  

 d: = v+u 

Code sequence for the example: