Q1) What is a red black tree?

A1) The self-balancing binary search tree has a category called the Red Black Tree. Rudolf Bayer used the phrase "symmetric binary B-trees".

A red-black tree is a Binary tree in which each node contains a color attribute, either red or black, as an additional attribute. Red-black trees ensure that no simple path from the root to a leaf is longer than twice as long as any other by checking the node colors, ensuring that the tree is generally balanced.

A red-black tree is a self-balancing binary search tree with one extra bit at each node, which is commonly read as the color (red or black). These colors are used to keep the tree balanced as insertions and deletions are made. The tree's balance isn't ideal, but it's good enough to cut down on searching time and keep it around O(log n), where n is the total number of components in the tree. Rudolf Bayer invented this tree in 1972.

It's worth noting that, because each node only needs 1 bit of memory to store the color information, these trees have the same memory footprint as a traditional (uncoloured) binary search tree.

A binary search tree with the following red-black features is known as a red-black tree:

●      Every node has a red or black color.

●      Every (NULL) leaf is black.

●      Both of a node's children are black if it is red.

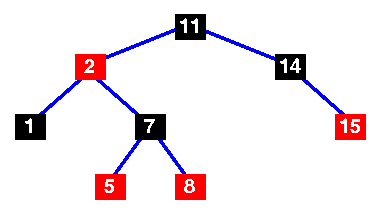
Fig 1: Red black tree

Q2) Write the property of the red black tree?

A2) Properties of Red black tree

●      A Binary Search Tree is required for the Red - Black Tree.

●      The ROOT node must be BLACK in color.

●      The offspring of the Red colored node must be painted in black. (There should not be two RED nodes in a row.)

●      There should be the same number of BLACK colored nodes in all of the tree's routes.

●      The color RED must be used to insert each new node.

●      Each leaf (for example, the NULL node) must be colored BLACK.

Q3) What is a B- tree?

A3) An extended binary tree is a sort of binary tree in which all of the original tree's null subtrees are replaced with special nodes known as external nodes, while other nodes are known as internal nodes.

The internal nodes are represented by circles, whereas the external nodes are represented by boxes. ​

It is not required that all nodes have the same number of children, but each node must include m/2 nodes.

The following graphic depicts a B tree of order 4.

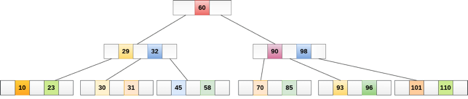
Fig 2: B tree

Any attribute of B Tree may be violated while performing some operations on it, such as the number of minimum children a node can have. The tree may split or unite in order to keep the features of B Tree.

Application of B tree

Because accessing values held in a huge database that is saved on a disk is a very time consuming activity, B tree is used to index the data and enable fast access to the actual data stored on the disks.

In the worst situation, searching an unindexed and unsorted database with n key values takes O(n) time. In the worst-case scenario, if we use B Tree to index this database, it will be searched in O(log n) time.

Q4) Write the operation of B-tree?

A4) Searching

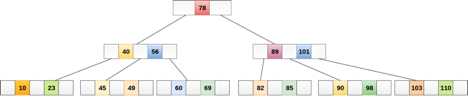
B Trees are comparable to Binary Search Trees in terms of searching. For example, let's look for item 49 in the B Tree below. The procedure will go somewhat like this:

The height of the tree affects the search in a B tree. To search any element in a B tree, the search technique requires O(log n) time.

Inserting

At the leaf node level, insertions are made. In order to place an item into B Tree, the following algorithm must be followed.

●      In the rising sequence of elements, add the new element.

●      At the middle, divide the node into two nodes.

●      The median element should be pushed up to its parent node.

●      If the parent node has the same m-1 number of keys as the child node, split it as well.

Deletion

At the leaf nodes, deletion is also conducted. It can be a leaf node or an inside node that needs to be destroyed. In order to delete a node from a B tree, use the following algorithm.

●      If the left sibling has more than m/2 elements, shift the intervening element down to the node where the key is deleted and push the largest element up to its parent.

●      If the right sibling has more than m/2 items, shift the intervening element down to the node where the key is deleted and push the smallest element up to the parent.

4.     Create a new leaf node by merging two leaf nodes and the parent node's intervening element if neither sibling has more than m/2 elements. If the parent has less than m/2 nodes, repeat the operation on the parent as well.

5.     If the node to be destroyed is an internal node, its in-order successor or predecessor should be used instead. The process will be the same as the node being deleted from the leaf node because the successor or predecessor will always be on the leaf node.

Q5) Explain binomial heaps?

A5) A collection of Binomial Trees is known as a Binomial Heap. A binomial tree Bk is a recursively defined ordered tree. A single node makes up a binomial Tree B0.

A binomial tree is one in which Bk is an ordered tree defined recursively, with k being the binomial tree's order.

●      When the binomial tree is represented as B0, there is just one node in the tree.

●      In general, Bk is made up of two binomial trees, Bk-1 and Bk-1, which are linked together so that one tree becomes the left subtree of another.

A Bk binomial tree is made up of two Bk-1 binomial trees. That are interconnected. The leftmost child of one's root is the leftmost child of the other's root.

Fig 3: Binomial tree

Below are some examples of binomial piles.

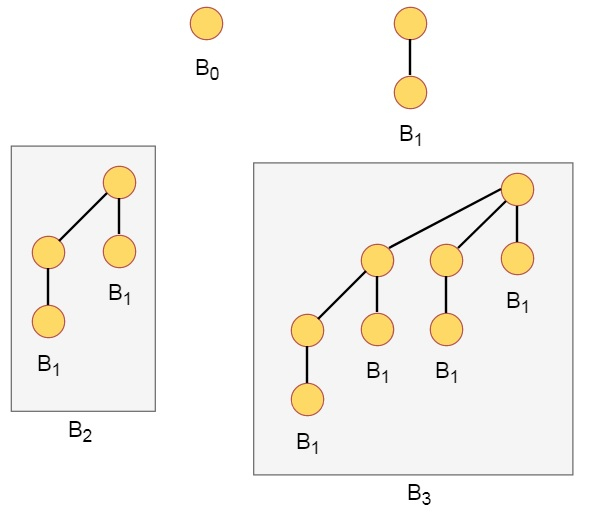
Fig 4: Example

The following are some of the attributes of binomial trees:

●      There are 2k nodes in a binomial tree with Bk.

●      The tree's height is k.

●      There are exactly

(JK)

For all I in the range 0 to k, there are precisely nodes at depth i.

Operation on binomial heap

Creating a new binomial heap: When we construct a new binomial heap, it takes only O(1) time since we are creating the head of the heap, which has no elements tied to it.

Finding the minimum key: As we all know, a binomial heap is a collection of binomial trees, each of which meets the property of min heap, which indicates that the root node has the smallest value. To obtain the minimum key, we must compare only the root node of all binomial trees. Finding a minimum key has an O time complexity (logn).

Union of two binomial heap: We can easily find the union of two binomial heaps if we wish to join two binomial heaps. Finding a union has an O time complexity (logn).

Inserting a node: Inserting a node has an O time complexity (logn).

Extracting minimum key: Removing a minimal key has an O time complexity (logn).

Decreasing a key: The binomial tree does not satisfy the min-heap when the key value of any node is altered. In order to meet the min-heap property, some rearrangements are required. O would be the time complexity (logn).

Deleting a node:  Delete a node has an O time complexity (logn).

Q6) Describe Fibonacci heaps?

A6) Fibonacci heaps, like Binomial heaps, are collections of trees. They're based on binomial piles, but only roughly. Unlike trees in binomial heaps, which are ordered, trees in Fibonacci heaps are rooted but not in any particular order.

In Fibonacci heaps, each node x has a pointer p[x] to its parent, as well as a pointer child[x] to any of its children. The children of x are linked together in the child list of x, a circular doubly linked list. Each kid y in a child list has left[y] and right[y] pointers that point to y's left and right siblings. Left[y] = right[y] = y if node y is the sole child. In a child list, the sequence in which siblings appear is random.

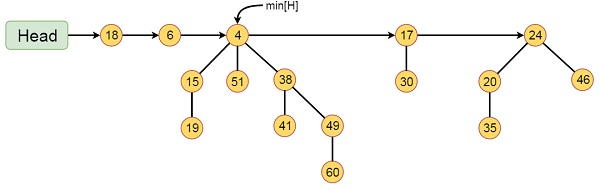
Fig 5: Example of Fibonacci heaps

This Fibonacci Heap H has 16 nodes and five Fibonacci Heaps. The root list is indicated by the line with an arrowhead. The list's minimum node is designated by min[H], which holds 4.

Fibonacci heaps are used extensively in asymptotically fast algorithms for issues such as computing minimal spanning trees, discovering single source of shortest pathways, and so on.

Properties

The following are some of the most important characteristics of a Fibonacci heap:

●      It's a collection of heap-ordered trees with a minimum size. (In other words, the parent is always smaller than the kids.)

●      At the smallest element node, a pointer is kept.

●      It is made up of a number of clearly designated nodes. (Reduce key operation.)

●      The trees in a Fibonacci heap are not in any particular order, yet they are all rooted.

Q7) Explain trie?

A7) The word "Trie" is an abbreviation for "retrieval." The set of strings is stored in a sorted tree-based data structure called a trie. Each node has the same number of pointers as the number of characters in the alphabet. It may use the prefix of a word to look up that word in the dictionary. If we suppose that all strings are made up of the letters a through z from the English alphabet, each trie node can have a maximum of 26 points.

The digital tree, or prefix tree, is another name for Trie. The key with which a node is associated is determined by its position in the Trie.

Properties

●      The null node is always represented by the trie's root node.

●      Every node's child is arranged alphabetically.

●      A maximum of 26 children can be found in each node (A to Z).

●      Except for the root, each node can store one letter of the alphabet.

The bell, bear, bore, bat, ball, stop, stock, and stack are all represented by trie in the diagram below.

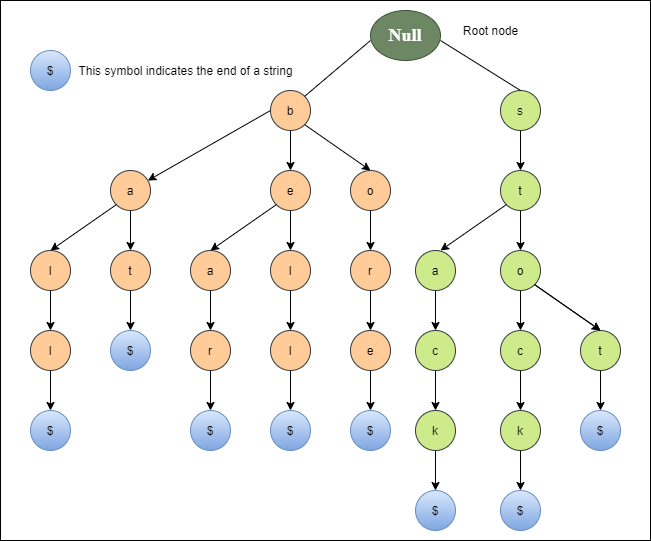
Fig 6: Tries

Operation

In the Trie, there are three operations:

Insertion of a node

Inserting a new node into the trie is the initial step. Before we begin the implementation, there are a few things to keep in mind:

●      In the Trie node, each letter of the input key (word) is entered separately. Children are nodes that point to the next level of Trie nodes.

●      The key character array serves as a child index.

●      Set the present node to the referenced node if the present node already has a reference to the present letter. Create a new node, set the letter to the same as the current letter, and even start the current node with this new node if necessary.

●      The depth of the trie is determined by the length of the characters.

Searching a node

The search for a node in a Trie is the second operation. The searching and inserting operations are very similar. The trie's search operation is used to find a key.

Deletion of a node

The deletion of a node in the Trie is the third operation. Before we start the implementation, there are a few things to keep in mind:

Q8) Write short notes on the skip list?

A8) A skip list is a data structure that uses a hierarchy of linked lists to store a sorted list of things by connecting increasingly sparse subsequences of the items. A skip list allows for a more efficient item lookup operation. The skip list data structure goes over a large number of elements in a single step, which is why it's called a skip list.

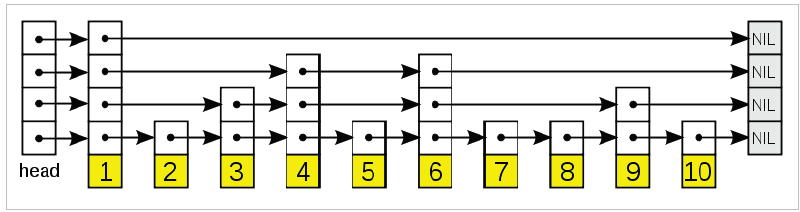
In a nutshell, skip lists are a type of linked list that enables for quick searching. It is made up of a base list that holds the items and a tower of lists that maintains a linked hierarchy of subsequences, each skipping over fewer elements.

Q9) What are the operation of the skip list?

A9) The operations performed on the Skip list are listed below.

Insertion

We must first decide on the nodes level before we begin entering entries into the skip list. Each element in the list is represented by a node, whose level is chosen at random during list insertion. The number of elements in a node has no bearing on the level. The following algorithm determines the node's level.

RandomLevel()

Lvl:= 1

//random() that returns a random value in [0...1)

While random() < p and lvl < MaxLevel do

Lvl:= lvl + 1

Return lvl 

The number of levels in the skip list is limited by MaxLevel. It can be calculated using the formula – L(N) = logp/2 (N). The procedure above ensures that the random level will never exceed MaxLevel. The fraction of nodes with level I pointers who also have level i+1 pointers is p, and the number of nodes in the list is N.

Pseudocode For Insertion

Insert(list, searchKey)

Local update[0...MaxLevel+1]

x:= list -> header

For i:= list -> level downto 0 do

While x -> forward[i] -> key  forward[i]

Update[i]:= x

x:= x -> forward[0]

Lvl:= randomLevel()

If lvl > list -> level then

For i:= list -> level + 1 to lvl do

Update[i]:= list -> header

List -> level:= lvl

x:= makeNode(lvl, searchKey, value)

For i:= 0 to level do

x -> forward[i]:= update[i] -> forward[i]

Update[i] -> forward[i]:= x

Searching

Searching for an element is analogous to searching for a location to put an element in a Skip list. The essential concept is that if –

●      If the element adjacent to the rightmost element (update[0]) has a key equal to the search key at the lowest level (0), we have found the key; otherwise, failure.

Pseudocode For Searching:

Search(list, searchKey)

x:= list -> header

-- loop invariant: x -> key  level downto 0 do

While x -> forward[i] -> key  forward[i]

x:= x -> forward[0]

If x -> key = searchKey then return x -> value

Else return failure

Deletion

The deletion of an element k is preceded by the use of the above-mentioned search procedure to locate the element in the Skip list. Once the element has been discovered, the pointers are rearranged to remove the element from the list, just like in a singly linked list. We start at the bottom and work our way up until the element next to update[i] is not k. There may be levels with no elements when an element is deleted, thus we'll eliminate these levels as well by lowering the level of the Skip list.

Pseudocode For Deletion

Delete(list, searchKey)

Local update[0..MaxLevel+1]

x:= list -> header

For i:= list -> level downto 0 do

While x -> forward[i] -> key  forward[i]

Update[i]:= x

x:= x -> forward[0]

If x -> key = searchKey then

For i = 0 to list -> level do

If update[i] -> forward[i] ≠ x then break

Update[i] -> forward[i]:= x -> forward[i]

Free(x)

While list -> level > 0 and list -> header -> forward[list -> level] = NIL do

List -> level:= list -> level – 1

Q10) Write the difference between red black tree and AVL tree?

A10) Difference between Red black tree and AVL tree

Q11) Write the difference between B tree and B+tree?

A11) Difference between B tree and B+ tree