Image Restoration
Q1) Describe image restoration?
A1) Image restoration is the operation of taking a corrupt/noisy image and estimating the clean, original image. Corruption may come in many forms such as motion blur, noise, and camera misfocus. Image restoration is performed by reversing the process that blurred the image and such is performed by imaging a point source and use the point source image, which is called the Point Spread Function (PSF) to restore the image information lost to the blurring process.
Image restoration is different from image enhancement in that the latter is designed to emphasize features of the image that make the image more pleasing to the observer, but not necessarily to produce realistic data from a scientific point of view. Image enhancement techniques (like contrast stretching or de-blurring by the nearest neighbour procedure) provided by imaging packages use no a priori model of the process that created the image.
With image, enhancement noise can effectively be removed by sacrificing some resolution, but this is not acceptable in many applications. In a fluorescence microscope, the resolution in the z-direction as bad as it is. More advanced image processing techniques must be applied to recover the object.
The objective of image restoration techniques is to reduce noise and recover resolution loss Image processing techniques are performed either in the image domain or the frequency domain. The most straightforward and conventional technique for image restoration is deconvolution, which is performed in the frequency domain and after computing the Fourier transform of both the image and the PSF and undo the resolution loss caused by the blurring factors. This deconvolution technique, because of its direct inversion of the PSF which typically has poor matrix condition number, amplifies noise and creates an imperfect deblurred image. Also, conventionally the blurring process is assumed to be shift-invariant. Hence more sophisticated techniques, such as regularized deblurring, have been developed to offer robust recovery under different types of noises and blurring functions. It is of 3 types: 1. Geometric correction 2. Radiometric correction 3. Noise removal
Q2) Define erlang (gamma) noise? With the help of graph.
A2)
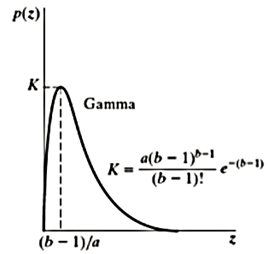
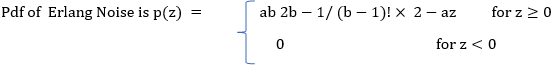
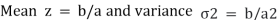
Exponential noise
The pdf of this noise is
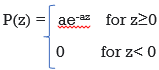
where a>0
Mean z = 1/a and variance σ2 = 1/ a2
This is a special case of Erlang Noise with b=1
Uniform Noise
PDF of uniform noise is given by

Mean = z = a+b/2
Variance = σ2 = (b-a)2/12
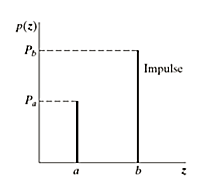
Impulse (Salt and Pepper Noise)
PDF of impulse noise is
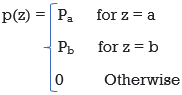
If b>a, intensity b will appear as alight dot in the image a will appear as dark dot




Periodic Noise

Restoration in the presence of noise only-Spatial filtering

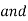
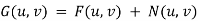
Q3) What do you mean by arithmetic mean filter?
A3) This is the simplest of the mean filters. Let Sxv represent the set of coordinates in a rectangular sub-image window of size m X n, centered at the point (x, y). The arithmetic means filtering process computes the average value of the corrupted image g (x, y) in the area defined by Sxy. The value of the restored image at any point (x, y) is simply the arithmetic mean computed using the pixels in the region defined by S. In other words.
fᵔ (x, y) = 1/mn ∑ (s.t) S xy g (s, t )
This operation can be implemented using a convolution mask in which ail coefficients have a value of 1/mn. As discussed in Section 3.6.1, a mean filter simply smoothes local variations in an image. Noise is reduced as a result of blurring.
Q4) What is geometric mean filter?
A4) An image restored using a geometric mean filter is given by the expression
fᵔ (x, y) = π(s.t) ᵋ S xy g(s, t) 1/mn
Here, each restored pixel is given by the product of the pixels in the sub-image window, raised to the power 1/mn. As shown in Example 52, a geometric mean filter achieves smoothing comparable to the arithmetic mean filter, but it tends to lose less image detail in the process.
Q5) Define Harmonic mean filter?
A5) The harmonic mean filtering operation is given by the expression
fᵔ (x, y) = mn / ∑ (s.t) ᵋ S xy 1/ g (s, t )
The harmonic mean filter works well for salt noise but fails for pepper noise. It does well also with other types of noise like Gaussian noise.
Q6) What is Contraharmonic mean filter?
A6) The contraharmonic mean filtering operation yields a restored image based on the expression
fᵔ (x, y) = ∑ (s.t) ᵋ S xy g (s, t )Q+1/ ∑ (s.t) ᵋ S xy g (s, t )Q
where Q is called the order of the filter. This filter is well suited for reducing or virtually eliminating the effects of salt-and-pepper noise. For positive values of Q, the filter eliminates pepper noise. For negative values of Q, it eliminates salt noise. It cannot do both simultaneously. Note that the contraharmonic filter reduces to the arithmetic mean filter if Q = 0, and to the harmonic mean filter if Q = - 1
Q7) Define Median Filter?
A7) The best-known order-statistics filter is the median filter, which, as its name implies, replaces the value of a pixel by the median of the gray levels in the neighborhood of that pixel:
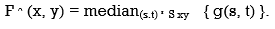
The original value of the pixel is included in the computation of the median. Median filters are quite popular because, for certain types of random noise, they provide excellent noise-reduction capabilities, with considerably less blurring than linear smoothing filters of similar size. Median filters are particularly effective in the presence of both bipolar and unipolar impulse noise. In fact, as Example 5.3 shows, the median filter yields excellent results for images corrupted by this type of noise.
Q8) Describe Max and min filter?
A8) Although the median filter is by far the order-statistics filter most used in image processing.it is by no means the only one. The median represents the 50th percentile of a ranked set of numbers, but the reader will recall from basic statistics that ranking lends itself to many other possibilities. For example, using the 100th percentile results in the so-called max filter given by:
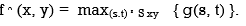
This filter is useful for finding the brightest points in an image. Also, because pepper noise has very low values, it is reduced by this filter as a result of the max selection process in the sub-image area S. The 0th percentile filter is the Min filter.
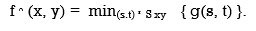
Q9) What do you mean by Band rejects filters?
A9) The BANDREJECT_FILTER function applies a low-reject, high-reject, or band-reject filter on a one-channel image.
A band-reject filter is useful when the general location of the noise in the frequency domain is known. A band-reject filter blocks frequencies within the chosen range and lets frequencies outside of the range pass through.
The following diagrams give a visual interpretation of the transfer functions:
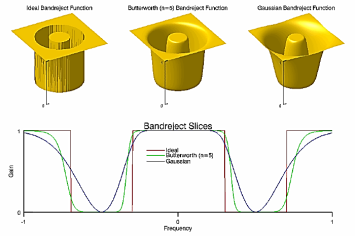
Fig – Band reject
This routine is written in the IDL language. Its source code can be found in the file bandreject_filter.pro in the lib subdirectory of the IDL distribution.
Result = BANDREJECT_FILTER (ImageData, LowFreq, HighFreq [, /IDEAL] [, BUTTERWORTH=value] [, /GAUSSIAN])
Returns a filtered image array of the same dimensions and type as ImageData.
A two-dimensional array containing the pixel values of the input image.
The lower limit of the cut-off frequency band. This value should be between 0 and 1 (inclusive) and must be less than HighFreq.
The upper limit of the cut-off frequency band. This value should be between 0 and 1 (inclusive) and must be greater than LowFreq.
Q10) Describe IDEAL keyword in band reject filter?
A10) Set this keyword to use an ideal band-reject filter. In this type of filter, frequencies outside of the given range are passed without attenuation, and frequencies inside of the given range are blocked. This behavior makes the ideal band-reject filters very sharp.
The centered Fast Fourier Transform (FFT) is filtered by the following function, where DL is the lower bound of the frequency band, DH is the upper bound of the frequency band, and D(u,v) is the distance between a point (u,v) in the frequency domain and the center of the frequency rectangle:

Q11) Describe the keyword BUTTERWORTH in band reject filter?
A11) Set this keyword to the dimension of the Butterworth filter to apply to the frequency domain. With a Butterworth band-reject filter, frequencies at the center of the frequency band are completely blocked and frequencies at the edge of the band are attenuated by a fraction of the maximum value. The Butterworth filter does not have any sharp discontinuities between passed and filtered frequencies.
Note: The default for BANDREJECT_FILTER is BUTTERWORTH=1.
The centered FFT is filtered by one of the following functions, where D0 is the center of the frequency
Low-reject (DL = 0, DH < 1): H (u, v) = 1 – 1/ 1+[D/DH]2n
Band -reject (DL > 0, DH < 1): H (u, v) = 1/ 1+[(DW)/ (D2- D20]2n
High- reject (DL > 0, DH = 1): H (u, v) = 1 – 1/ 1+ [DL / D]2n
cy band, W is the width of the frequency band, D=D (u, v) is the distance between a point (u, v) in the frequency domain and the center of the frequency rectangle, and n is the dimension of the Butterworth filter:
Note: A low Butterworth dimension is close to Gaussian, and a high Butterworth dimension is close to Ideal.
Q12) Describe the keyword GAUSSIAN in band reject filter?
A12) Set this keyword to use a Gaussian band-reject filter. In this type of filter, the transition between unfiltered and filtered frequencies is very smooth.
The centered FFT is filtered by one of the following functions, where D0 is the center of the frequency band, W is the width of the frequency band, and D=D(u,v) is the distance between a point (u,v) in the frequency domain and the center of the frequency rectangle:
Low – reject (DL = 0, DH< 1): H (u, v) = 1-e-D2/ (2 D2H)
Band – reject (DL = 0, DH< 1): H (u, v) = e-[( D2- D20) / (DW)] 2
High – reject (DL = 0, DH = 1): H (u, v) = 1- e-D2 / (2DL. 2)
Q13) Define Notch filter?
A13) Notch filters:
Repetitive noise in an image is sometimes seen as a bright peak somewhere other than the origin. You can suppress such noise effectively by carefully erasing the peaks. One way to do this is to use a notch filter to simply remove that frequency from the picture. This technique is very common in sound signal processing where it is used to remove mechanical or electronic hum, such as the 60Hz hum from AC power. Although it is possible to create notch filters for common noise patterns, in general notch filtering is an ad hoc procedure requiring a human expert to determine what frequencies need to be removed to clean up the signal.
The following is an example of removing synthetic spectral "noise" from an image.

The above images were created using four M-files(paddedsize.m, lpfilter.m, dftuv.m, and notch.m), noiseball.png, and the following MATLAB calls
footBall=imread('noiseball.png');
imshow(footBall)
%Determine good padding for Fourier transform
PQ = paddedsize(size(footBall));
%Create Notch filters corresponding to extra peaks in the Fourier transform
H1 = notch('btw', PQ(1), PQ(2), 10, 50, 100);
H2 = notch('btw', PQ(1), PQ(2), 10, 1, 400);
H3 = notch('btw', PQ(1), PQ(2), 10, 620, 100);
H4 = notch('btw', PQ(1), PQ(2), 10, 22, 414);
H5 = notch('btw', PQ(1), PQ(2), 10, 592, 414);
H6 = notch('btw', PQ(1), PQ(2), 10, 1, 114);
% Calculate the discrete Fourier transform of the image
F=fft2(double(footBall),PQ(1),PQ(2));
% Apply the notch filters to the Fourier spectrum of the image
FS_football = F.*H1.*H2.*H3.*H4.*H5.*H6;
% convert the result to the spatial domain.
F_football=real(ifft2(FS_football));
% Crop the image to undo padding
F_football=F_football(1:size(footBall,1), 1:size(footBall,2));
%Display the blurred image
figure, imshow(F_football,[])
% Display the Fourier Spectrum
% Move the origin of the transform to the center of the frequency rectangle.
Fc=fftshift(F);
Fcf=fftshift(FS_football);
% use abs to compute the magnitude and use log to brighten display
S1=log(1+abs(Fc));
S2=log(1+abs(Fcf));
figure, imshow(S1,[])
figure, imshow(S2,[])
Q14) What do you mean by optimum Notch filtering?
A14) When several interference components are present or if the interference has broad skirts a simply notch filter may remove too much image information.
One solution is to use an optimum filter that minimizes local variances of the restored estimate.
Such “smoothness” constraints are often found in optimum filter design
1. Manually place a notch pass filter HNP at each noise spike in the frequency domain. The Fourier transform of the interference noise pattern is
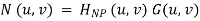
2. Determine the noise pattern in the spatial domain
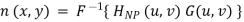
3. Conventional thinking would be to simply eliminate noise by subtracting the periodic noise from the noisy image

4. To construct an optimal filter consider
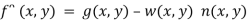
Where w (x, y) is a weighting function.
 5. We use the weighting function w (x, y) to minimize the variance 2(x, y) with respect to w (x, y)
5. We use the weighting function w (x, y) to minimize the variance 2(x, y) with respect to w (x, y)
We only need to compute this for one point in each non-overlapping neighborhood.
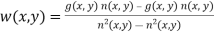
g (x, y) n (x, y) Mean product of noisy images and noise
n (x, y) Mean noise output from the notch filter
n2(x, y) Mean squared noise output from the notch filter
Q15) What do you mean by inverse filtering?
A15) If a degraded image is given by degradation + noise
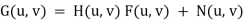
•Estimate the image by dividing by the degradation function H(u,v)
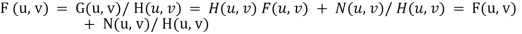
We can never recover F (u, v) exactly:
1.N(u, v) is not known since (x, y) is a r.v. — estimated
2.If H (u, v) ->0 then the noise term will dominate. Helped by restricting the analysis to (u, v) near the origin.
Modeling of Degradation

F᷈ (u, v) = F(u, v) + N(u, v)/ H(u, v) , where H(u, v) = e-k{( u- m/2 )2 +( v-N/2) 2} 5/6
Q16) What is wiener filtering?
A16) The best estimate F᷈ (u, v) is then given by
F᷈ (u, v) = [ H*(u, v) Sf (u, v) / Sf (u, v) |H (u, v)|2 + Sn (u, v)] G(u, v) = [ H*(u, v) / |H(u, v)|2 + Sn (u, v)/ Sf (u, v) ] G(u, v)
F᷈ (u, v) = [1/H (u, v) × |H (u, v)|2 / |H(u, v)|2 + Sn(u, v) / Sf (u, v) ] G(u, v)
H (u, v) = degradation function
H*(u, v) = complex conjugate of H
|H (u, v)| = H*(u, v) H(u, v)
Sn (u, v) = |N (u, v)|2 = power spectrum of noise (estimated)
Sf (u, v) = |F (u, v)|2 = power spectrum of original image (not known)
Modeling of Degradation
Inverse filtering
N(u, v)/ H(u, v)
Radially limit at D0 = 75
Wiener filtering
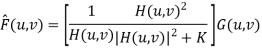
In practice we don’t know the power spectrum Sf(u, v) = |F(u, v)|2 of the original image so we replace the Sn / Sf term with a constant K which we vary
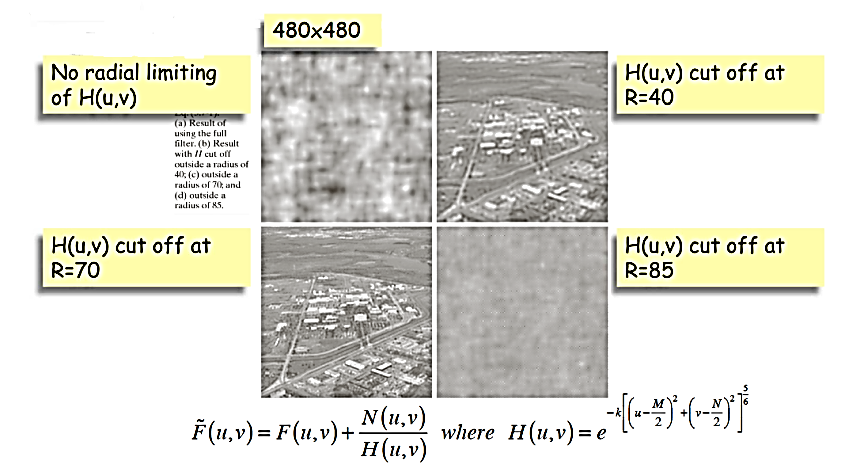
Inverse filtering
N (u, v)/ H (u, v)
Radially limit at D0 = 75
Wiener filtering

In practice we don’t know the power spectrum Sf (u, v) = |F (u, v)|2 of the original image so we replace the Sn / Sf term with a constant K which we vary