Module 2
Differential Calculus- I
Q 1: Verify Rolle’s theorem for the function f(x) = x2 for 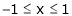
Solution:
Here f(x) = x2; 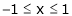
i) Since f(x) is algebraic polynomial which is continuous in [-1, 1]
ii) Consider f(x) = x2
Diff. w.r.t. x we get
f'(x) = 2x
Clearly f’(x) exists in (-1, 1) and does not becomes infinite.
iii) Clearly
f(-1) = (-1)2 = 1
f(1) = (1)2 = 1
 f(-1) = f(1).
f(-1) = f(1).
Hence by Rolle’s theorem, there exist 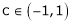 such that
such that
f’(c) = 0
i.e. 2c = 0
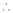 c = 0
c = 0
Thus 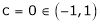 such that
such that
f'(c) = 0
Hence Rolle’s Theorem is verified.
Q 2: Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in 
Solution:
Here f(x) = ex(sin x – cos x); 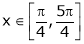
i) Ex is an exponential function continuous for every 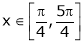 also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in
also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 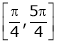 and Hence ex(sin x – cos x) is continuous in
and Hence ex(sin x – cos x) is continuous in 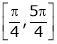 .
.
ii) Consider
f(x) = ex(sin x – cos x)
diff. w.r.t. x we get
f’(x) = ex(cos x + sin x) + ex(sin x + cos x)
= ex[2sin x]
Clearly f’(x) is exist for each 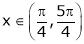 & f’(x) is not infinite.
& f’(x) is not infinite.
Hence f(x) is differentiable in  .
.
iii) Consider

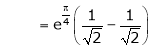
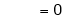
Also,
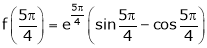
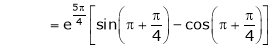

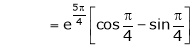
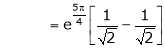

Thus 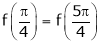
Hence all the conditions of Rolle’s theorem are satisfied, so there exist 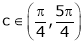 such, that
such, that
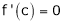
i.e. 
i.e. sin c = 0

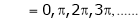
But
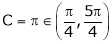
Hence Rolle’s theorem is verified.
Q 3 Verify whether Rolle’s theorem is applicable or not for
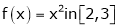
Solution:
Here f(x) = x2; 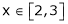
i) X2 is an algebraic polynomial hence it is continuous in [2, 3]
ii) Consider
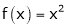

F’(x) exists for each 
iii) Consider
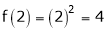
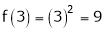
Thus 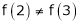 .
.
Thus all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3]
Q 4 Verify the Lagrange’s mean value theorem for

Solution:
Here 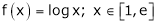
i) Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]
ii) Consider f(x) = log x.
Diff. w.r.t. x we get,

Clearly f’(x) exists for each value of 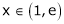 & is finite.
& is finite.
Hence all conditions of LMVT are satisfied Hence at least 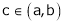
Such that
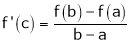
i.e. 
i.e. 
i.e. 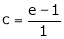
i.e. 
since e = 2.7183
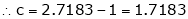
Clearly c = 1.7183 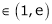
Hence LMVT is verified.
Q5: Verify mean value theorem for f(x) = tan-1x in [0, 1]
Solution:
Here  ;
; 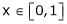
i) Clearly 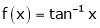 is an inverse trigonometric function and hence it is continuous in [0, 1]
is an inverse trigonometric function and hence it is continuous in [0, 1]
ii) Consider 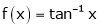
diff. w.r.t. x we get,
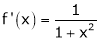
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite
Hence all conditions of LMVT are satisfied, Thus there exist 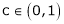
Such that
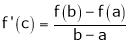
i.e. 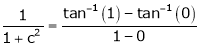
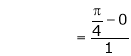
i.e. 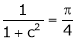
i.e. 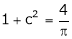
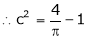
i.e. 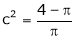
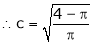
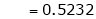
Clearly 
Hence LMVT is verified.
Q 6: Prove that
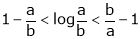
And hence show that
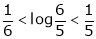
Solution:
Let 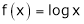 ;
; 
i) Clearly 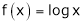 is a logarithmic function and hence it is continuous also
is a logarithmic function and hence it is continuous also
ii) Consider 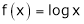
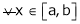
diff. w.r.t. x we get,
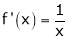
Clearly f’(x) exist and finite in (a, b) Hence f(x) is continuous and differentiable in (a, b). Hence by LMVT 
Such that
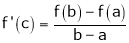
i.e. 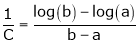
i.e. 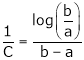
since
a < c < b

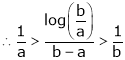
i.e. 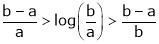
i.e. 
i.e. 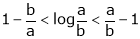
i.e. 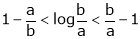
Hence the result
Now put a = 5, b = 6 we get

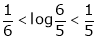
Hence the result
Q 7: Prove that 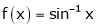 ,
, 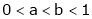 use mean value theorem to prove that,
use mean value theorem to prove that,
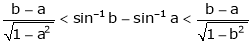
Hence show that
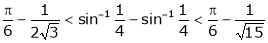
Solution:
i) Let f(x) = sin-1x; 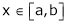
ii) Clearly f(x) is inverse trigonometric function and hence it is continuous in [a, b]
iii) Consider f(x) = sin-1x
diff. w.r.t. x we get,
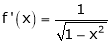
Clearly f’(x) is finite and exists for 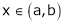 . Hence by LMVT,
. Hence by LMVT, 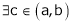 such that
such that

i.e. 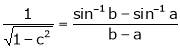
since a < c < b
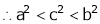
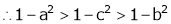
i.e. 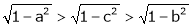
i.e. 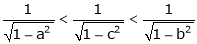
i.e. 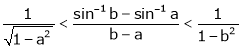
i.e. 
Hence the result
Put 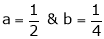 we get
we get
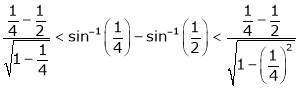
i.e. 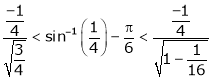
i.e. 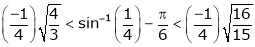
i.e. 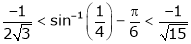
i.e. 
Hence the result
Q 8: Use LaGrange’s mean value theorem to determine a point P on the curve y=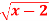
where the tangent is parallel to the chord joining (2,0) and (3,1)
solution:
consider y= 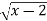 in [2,3]
in [2,3]
(i) Function is continuous in[2,3] as algebraic expression with positive exponent is continuous.
(ii) y’= 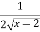 , y’ exists in (2,3) hence the function is derivable in (2,3)
, y’ exists in (2,3) hence the function is derivable in (2,3)
hence the condition of LMV theorem is satisfied.
Hence, there exists one c in (2,3) such that 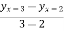 =
= 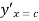
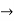
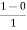 =
= 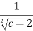
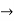 4(c-2) = 1
4(c-2) = 1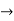 4c=9
4c=9 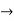 c= 4/9
c= 4/9
 for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)
for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)
Substituting in (i) we get,
Y= 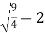 =
= 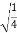 = ½
= ½
Q 9: Verify LaGrange’s mean value theorem for the following function
f(x) = 
putting x=a=2 and x=b=5 ,we get
f(2) = 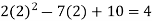
f(5) = 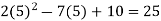
clearly,
f(2) 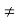 f(5)
f(5)
since f(x) is a polynomial function in x, then f(x) is continuous in [2,5].
And f(x) is polynomial in x, then it can be differentiate such that f’(x) = 4x-7
Then by LMV theorem there exists c 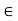 (2,5) such that’
(2,5) such that’
f’ (c) = 
4c-7 = 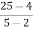
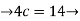 c=3.75
c=3.75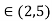
Hence Lagrange’s mean value theorem is verified for f(x) in [2,5].
Q 10: Verify Cauchy mean value theorems for 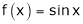 &
&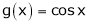 in
in 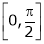
Solution:
Let 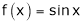 &
& ;
; 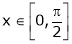
i) Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in 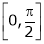
ii) Since 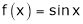 &
&
diff. w.r.t. x we get,
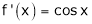 &
&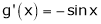
Clearly both f’(x) and g’(x) exist & finite in 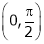 . Hence f(x) and g(x) is derivable in
. Hence f(x) and g(x) is derivable in 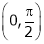 and
and
iii) 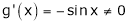

Hence by Cauchy mean value theorem, there exist at least 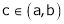 such that
such that
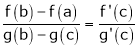
i.e. 
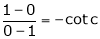
i.e. 1 = cot c

i.e. 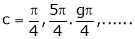
clearly 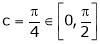
Hence Cauchy mean value theorem is verified.
Q 11: Considering the functions ex and e-x, show that c is arithmetic mean of a & b.
Solution:
i) Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b].
ii) Consider 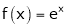 &
&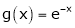
diff. w.r.t. x we get
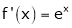 and
and 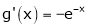
Clearly f(x) and g(x) are derivable in (a, b)
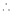 By Cauchy’s mean value theorem
By Cauchy’s mean value theorem 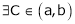 such that
such that
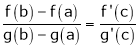
i.e. 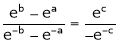
i.e. 
i.e. 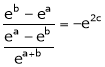
i.e. 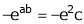
i.e. 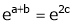
i.e. 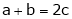

Thus 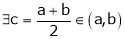
i.e. c is arithmetic mean of a & b.
Hence the result
Q 12: Show that 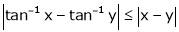
Prove that if 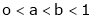
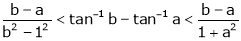 and Hence show that
and Hence show that

Verify Cauchy’s mean value theorem for the function x2 and x4 in [a, b] where a, b > 0
If for 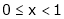 then prove that,
then prove that,
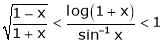
[Hint: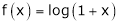 ,
, 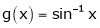 ]
]
Q 13: Find the nth derivative of sin3 x
Sol: we know that sin 3x= 3sin x 4sin3 x = sin3x = 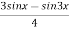
Differentiate n times w.r.t x,
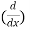 ( sin3 x) =
( sin3 x) = 
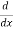 (3 sinx- sin3x)
(3 sinx- sin3x)
= ( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
Q 14: Find the nth derivative of sin 5x. sin 3x.?
Sol: let y = sin 5x.sin 3x=  ( sin 5x.sin 3x)
( sin 5x.sin 3x)
⇒y=  ( cos 2x - cos8x)
( cos 2x - cos8x)
⇒ y= ( cos 2x- cos8x )
( cos 2x- cos8x )
Differentiate n times w.r.t x,
Yn = 
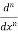 ( cos 2x - cos8x )
( cos 2x - cos8x )
⇒ yn =  ( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
Q 15: If y = ae n x + be –nx , then show that y2= n2y
Sol: Y= aenx + be-nx
y 1 = a.n.enx - b.n.e-nx
y2 = an2 enx – bn2 e-nx = n2 (ae nx+ be –nx)
y2= n2y.
Q 16: If y= e-kx/2(a cosnx+ b sinnx) then show that.,y2+ ky1+(n2+ k2/4)y =0
Sol : y= e-kx/2(a cosnx+ b sinnx)
Differentiating w.r.to. x.,
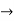 Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
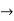 Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx)
Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx) 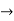 (1)
(1)
Differentiating w.r.to x.,
Y2+ k/2.y1 = ne-kx/2 (-k/2) ( -an sin nx + bn cos nx) + n e-kx/2(-an cosnx- bn sinnx).
= -(k/2) (y1+ k/2 y)- n2 y = - (k/2 y1)- ( k2/4)y- n2y.
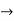 y2 + ky1 +(n2+ k2/4)y = 0.
y2 + ky1 +(n2+ k2/4)y = 0.
Q 17: If Y 2) = log( x +
2) = log( x + 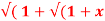 2) ) then show that (1 + x 2) y1 +xy =1
2) ) then show that (1 + x 2) y1 +xy =1
Sol: Y 2) = log( x +
2) = log( x + 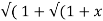 2) )
2) )
Differentiating w.r.to x.,
y.1/ 2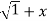 2 .2x+
2 .2x+ 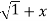 2. Y1.
2. Y1.
=(1+x ) y +xy = 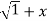 . 1/x
. 1/x 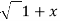 2 .
2 .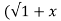 2) +x/
2) +x/ 2 =1
2 =1
Q 18: Sove the following using lebinitz rule:
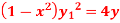
Solution:
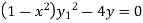
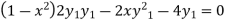
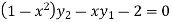
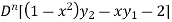 =0
=0
Q 19: Find the envelope of the family of the ellipses defined by the equation
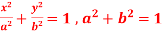
Solution:
The equation for the given family of curves can be writeen as
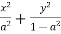 =1…..(1)
=1…..(1)
Where the semi axis a is the parameter and 0<a<1
Differentiating eq(1) w.r.to a is


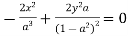

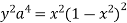
Take the square root of both sides of the equation:
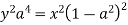
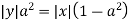
Express  from the last equation
from the last equation
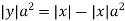
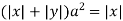
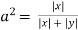
Substituting in the eq(1) we get
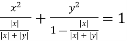
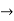
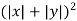 =1
=1
=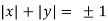
Q 20: Find the evolute for the following parabola y=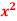
Solution:
For evoluting the parabola we have the following formulae,
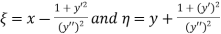
Substituting the given function we get

By eliminating the x in 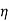 we getx =
we getx = 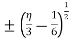
Substituting in 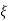 we get
we get 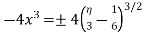
Therefore the required answer is 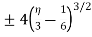
Q 21: For a given curve convert the point (2, ) from polar to Cartesian form
) from polar to Cartesian form
Solution:
r=2 and  =
=  we have,
we have,
x = rcos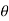 and y= rsin
and y= rsin
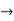 x= 2.cos
x= 2.cos = 2.1/2 = 1
= 2.1/2 = 1
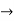 y = 2.sin
y = 2.sin = 2.
= 2.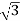 /2 =
/2 = 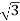
Therefore the required Cartesian point is (1,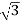 ).
).