Module 3

Differential Calculus-II

Q 1: Find the taylor series for the following:

Solution:

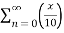
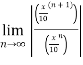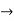
= <1

(x/10)<1 and (x/10) > -1

Therefore, radius of convergence is (-10,10)

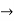  ROC =10

Q  2: f(n)5 =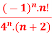

here the ROC is 4

example 2:

compute the Taylor series centered at zero for f(x)= sinx

solution:

f(x)=sinx               f(0)=0

f’(x)=cosx             f’(0)=1

f’’(x)=-sinx           f’’(0)=0

f’’’(x)= -cosx       f’’’(0)=-1

f(4)(x)= cosx        f(4) (0)= 1

applying taylor series we get

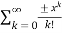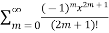T(x) =   =   = x-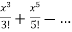

Thus turns out to converge x to sinx.

Q  3:

f(x)=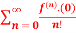

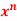
    = f(0)+f’(0)x+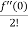 x2 + 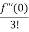x3 +......

    = 1+x+x2 +x3 + .....

=

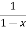
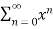
Q 4: Find the maclurins series for f(x)= ex

Solution:

To get maclurin series, we look at the Taylor series polynomials for f near 0 and let them keep going.

Considering for example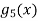

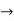
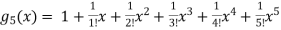
By maclurian series we get,

+

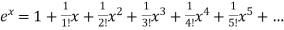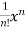
Q 5: Find out the maxima and minima of the function

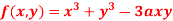
Solution:

   Given 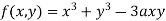    …(i)

         Partially differentiating (i) with respect to x we get

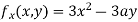    ….(ii)

         Partially differentiating (i) with respect to y we get

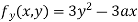    ….(iii)

          Now, form the equations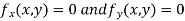

                    Using (ii) and (iii) we get

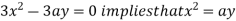
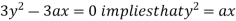
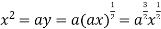          using above two equations

                     Squaring both side we get

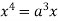
                      Or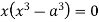 

                       This show that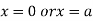

                         Also we get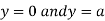

                 Thus we get the pair of value as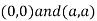

                  Now, we calculate

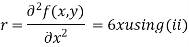
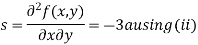
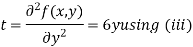
      Putting above values in

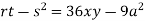
      At point (0,0)  we get

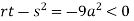
      So, the point (0,0) is a saddle point.

      At point 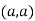we get

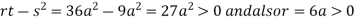
        So the point 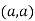is the minimum point where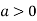

          In case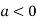 

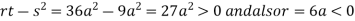
         So the point 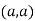is the maximum point where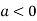

Q 6: Find the maximum and minimum point of the function

        Partially differentiating given equation with respect to and x and y then equate them to zero                 

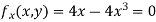
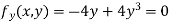
       On solving above we get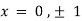 

         Also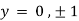

            Thus we get the pair of values (0,0), (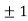,0) and (0,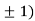

        Now, we calculate

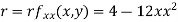
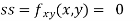
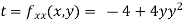
        At the point (0,0)

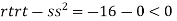
       So function has saddle point at (0,0).

       At the point (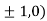

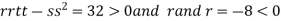
         So the function has maxima at this point (.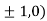

        At the point (0,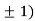

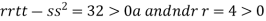
       So the function has minima at this point (0,.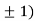

        At the point (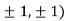

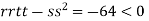
        So the function has an saddle point at (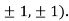

Q 7: Find the maximum and minimum value of

Let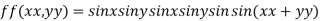

Partially differentiating given function with respect to x and y and equate it to zero

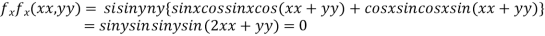  ..(i)

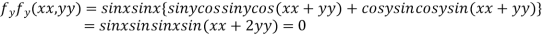    ..(ii)

      On solving (i) and (ii) we get

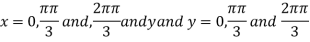
Thus pair of values are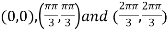

Now, we calculate

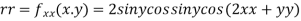
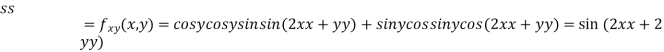
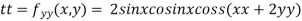
At the point (0,0)

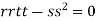
  So further investigation is required

On the x  axis y  = 0  , f(x,0)=0

On the line y=x,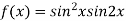

At the point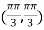

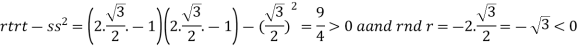
So that the given function has maximum value at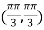

Therefore maximum value of given function

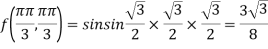
At the point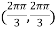

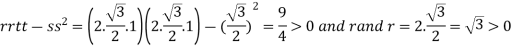
So that the given function has minimum value at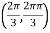

Therefore minimum value of the given function

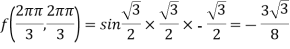
Q 8: Determine the Jaccobian matrix of the function f: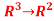  given by f(x,y,z)=(xy+2yz,2xy2z).

Solution:

We first f = (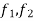) where 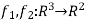given by f(x,y,z) = xy+2yz and 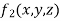= 2x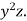we now compute the gradients of the following:

=

=

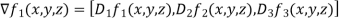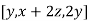
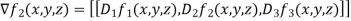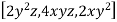
Then the Jacobian matrix is given by,

Df(x,y,z) =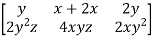

Q 9: Determine the Jacobian matrix of the function defined for all

 x=  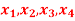 ( )   we have that,

f(x) = f(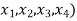

        =

        =

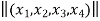
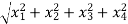
Since f is real valued function the Jacobian f is simply the gradient of f.the gradient of f is given by

   =

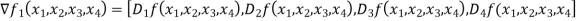
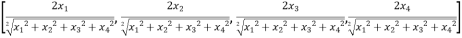
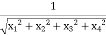 =          Therefore, the Jacobian f defined whenever x

Q 10: Suppose you are running a factor, producing some sort of widget that requires steel as a raw material.your costs are predominantly human labour,which is per hour for your workers,and the steel itself,which runs for $ 170 per ton.Suppose your revenue R is loosely modeled by the following equation:

R(h,s) = 200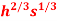

*h represents hour of labour

*s represents tons of steel,if your budget is $20,000, what is the maximum possible rvenue?

Solution:

The $ 20 per hour costs and $170 per hour ton steel costa tells us that the total cost of production in terms of h and s is,

20h+170s

Therefore the budget $20,000  can be translated to the constraint,

20h+170s

Since we need to maximize a function R(h,s), subject to a constraint,

20h+170s=20,000

The lagranges function is,

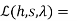20020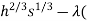h+170s  - 20,000)

Next we set the gradient 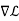equal to zero vector.

0 =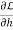

0=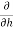  (20020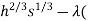h+170s  - 20,000))

0=20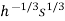0. -20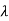

Now we derivative w.r.to s.,

0 =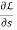

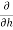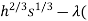0=0=  (20020h+170s  - 20,000))

0=20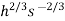0. -170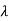

Now we set the partial derivation w.r.to., s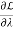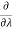

0 =

0=  (200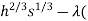20h+170s  - 20,000))

0 = -20h -170s+20,000

Putting together, the system of equations we need to solve

0 = 200  .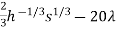

0 = 200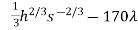

20h+170s = 20,000

Finally we get the values as,

h = 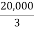= 666.667

s=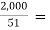 39.2157

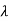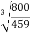= = 2.593