Unit – 2
Energy bands in intrinsic and extrinsic silicon
Q1) For a p-type Ge ni = 2.1x1019m-3 density of boron =3.2x1023 atoms m-3. The electron and hole mobility are 0.4 and 0.2 m2V-1s-1. Calculate conductivity before and after addition of boron?
A1) Before adding boron
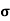 = q (p
= q (p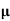 p+n
p+n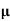 n)
n)
= ni q (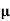 p+
p+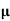 n) = 2.1x1019x1.6x10-19x(0.4+0.2)=2.016 S/m-1
n) = 2.1x1019x1.6x10-19x(0.4+0.2)=2.016 S/m-1
After adding boron
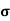 = q p
= q p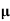 p
p
= 3.2x1023x1.6x10-19x0.2=10.24x103S/m-1
Q2) Determine the density of the donor atoms which have been added to the intrinsic Ge to make it a n-type material of resistivity 0.1x10-2ohm-m. Mobility of electron in n-type semiconductor is 0.5m2V-1s-1.
A2) 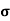 = q (n
= q (n n)
n)
n= 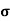 /q
/q n
n
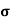 = 1/
= 1/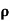
n= 1/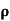 q
q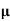 n = 1/(0.1x10-2x0.5x1.6x10-19) = 1.25x1022m-3
n = 1/(0.1x10-2x0.5x1.6x10-19) = 1.25x1022m-3
Q3) The intrinsic carrier density at room temperature in Ge is 3.4x1019m-3. If electron and hole mobilities are 0.4 and 0.2 m2V-1s-1 respectively. Calculate its resistivity?
A3) 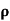 = 1/
= 1/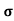
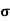 =ni q (
=ni q (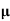 p+
p+ n) = 3.4x1019x 1.6x10-19(0.4+0.2) = 3.264S/m-1
n) = 3.4x1019x 1.6x10-19(0.4+0.2) = 3.264S/m-1
 = 1/
= 1/ = 1/3.264 = 0.31ohm-m
= 1/3.264 = 0.31ohm-m
Q4) The electron and hole mobilities in In-Sb are 6 and 0.2 m2V-1s-1 respectively. At room temperature resistivity of In-Sb is 2x10-4ohm-m. Find intrinsic carrier concentration assuming the material to be intrinsic?
A4) 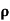 = 1/
= 1/
 =ni q (
=ni q (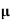 p+
p+ n)
n)
ni = 1/ 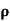 q (
q (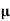 p+
p+ n) = 1/2x10-4x1.6x10-19(6+0.2) = 5.04x1021m-3
n) = 1/2x10-4x1.6x10-19(6+0.2) = 5.04x1021m-3
Q5) An electric field of 90Vm-1 is applied to n-type semiconductor. Determine the current density in sample given electron mobility 0.4 m2V-1s-1, n=5.9x1020m-3?
A5) J=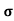 E
E
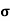 = nq
= nq n = 5.9x1020x1.6x10-19x0.4=37.36S/m-1
n = 5.9x1020x1.6x10-19x0.4=37.36S/m-1
J=3.39x103
Q6) Determine the density of the donor atoms which have been added to the intrinsic Ge to make it a n-type material of resistivity 0.5x10-2ohm-m. Mobility of electron in n-type semiconductor is 0.8m2V-1s-1.
A6) 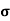 = q (n
= q (n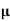 n)
n)
n= 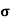 /q
/q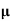 n
n
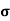 = 1/
= 1/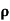
n= 1/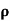 q
q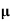 n = 1/(0.5x10-2x0.8x1.6x10-19) = 1.56x1021m-3
n = 1/(0.5x10-2x0.8x1.6x10-19) = 1.56x1021m-3
Q7) Calculate the drift current density in a semiconductor for a given electric field. For germanium sample at T=300oK where ND = 0 and NA =1x1015 cm-3 ni = 2.4x1013 cm-3. Assume electron and hole mobility to be 3900 cm2/V-sec and 1900 cm2/V-sec. Applied electric field is E= 40V/cm?
A7) As NA>>ND
p0 = ½ {(NA- ND) + (NA- ND)2+4ni2)1/2}
p0 = 5x1014cm-3
n= ni2/NA
n= 5.76x1011cm-3
J = q (p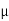 p+n
p+n n) E
n) E
For extrinsic p-type semiconductor
J = q NA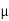 p E =1.6x10-19x1900x1015x40 =12.16 A/cm2
p E =1.6x10-19x1900x1015x40 =12.16 A/cm2
Q8) The resistance of a wire is 20 Ω. What will be new resistance, if it is stretched uniformly 8 times its original length?
A8) R1 = 20 Ω, R2=?
Let the original length (l1) be l.
The new length, l2 = 8l1 (i.e) l2 =8l
The original resistance, R = ρ [ l1 / A1]
The new resistance

Though the wire is stretched, its volume is unchanged.
Initial volume = Final volume
A1l1= A2l2 , A1l = A28l
A1 / A2 = 8l / l = 8
By dividing equation R2 by equation R1, we get

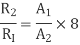
Substituting the value of A1/A2, we get
R2 / R1 = 8 ×8 = 64 2
R2 = 64 × 20=1280 Ω
Hence, stretching the length of the wire has increased its resistance.
Q9) Consider a rectangular block of metal of height A, width B and length C as shown in the figure.

If a potential difference of V is applied between the two faces A and B of the block (figure (a)), the current IAB is observed. Find the current that flows if the same potential difference V is applied between the two faces B and C of the block (figure (b)). Give your answers in terms of IAB.
A9)
In the first case, the resistance of the block
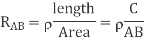
The current 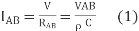
In the second case, the resistance of the block 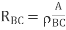
The current 
To express interms of
interms of 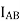 we multiply and divide equation (2) by AC we get
we multiply and divide equation (2) by AC we get

Since C>A, the current 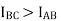
Q10) Compute the resistivity of the given material whose resistance is 2 Ω; area of cross-section and length are 25cm2 and 15 cm respectively?
A10)
R = 2 Ω
l = 15 cm = 0.15 m
A = 25 cm2 = 0.25 m2
Resistivity formula is
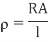

Q11) The length and area of wire are given as 0.2 m and 0.5 m2 respectively. The resistance of that wire is 3 Ω, calculate the resistivity?
A11)
Given
R = 3 Ω
l = 0.2 m and
A = 0.5 m2
Resistivity formula is
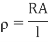
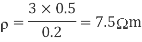
Q12) Determine thermal equilibrium of electron and hole concentration for an n-type silicon semiconductor at T=300oK where ND = 1x1016cm-3 and NA =0. Assume ni = 1.5 x 1010cm-3?
A12) The majority carrier concentration
n0 = ½ {(ND- NA) + (ND- NA)2+4ni2)1/2}
n0 = 1016 cm-3
The minority carrier concentration
p0 = ni2/ND
p0 = 2.25x x104 cm-3
Q13) Determine thermal equilibrium of electron and hole concentration for doping concentration at T=300oK where ND = 4x1013cm-3 and NA =0. Assume ni = 2.4 x 1013cm-3?
A13) The majority carrier concentration
n0 = ½ {(ND- NA) + (ND- NA)2+4ni2)1/2}
n0 =3.12x1013 cm-3
The minority carrier concentration
p0 = ni2/ND
p0 = 1.45x x1013 cm-3
Q14) Determine thermal equilibrium of electron and hole concentration in n-type semiconductor at T=300oK where ND = 2x1016cm-3 and NA =12x1015 cm-3. Assume ni = 1.5 x 1010cm-3?
A14) The majority carrier concentration
n0 = ½ {(ND- NA) + (ND- NA)2+4ni2)1/2}
n0 =4x1015 cm-3
The minority carrier concentration
p0 = ni2/ND
p0 = 11.25x x103 cm-3
Q15) The intrinsic carrier density is 1.5 × 1016 m–3. If the mobility of electron and hole are 0.13 and 0.05 m2 V–1 s–1, calculate the conductivity.
A15)
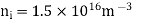
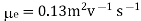
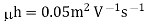
Conductivity 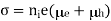
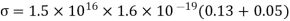
Conductivity 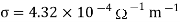
Q16) The Intrinsic carrier density at room temperature in Ge is 2.37 × 1019 m3 if the electron and hole mobilities are 0.38 and 0.18 m2 V–1 s–1 respectively, calculate the resistivity.
A16)

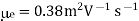
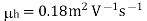
Conductivity 
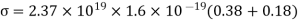
Conductivity 
Resistivity 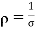
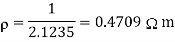
Q17) In a P-type germanium, ni = 2.1 × 1019 m–3density of boron 4.5 × 1023 atoms /m3. The electron and hole mobility are 0.4 and 0.2 m2 v–1 s–1 respectively. What is its conductivity before and after addition of boron atoms.
A17)
Given Intrinsic carrier concentration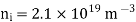
Mobility of electrons 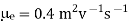
Mobility of holes 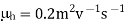
A) Conductivity before the addition of boron atoms

b) Conductivity after the addition of boron atoms, Boron is a P-type impurity atom.
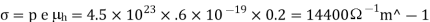
Q18) For an intrinsic Semiconductor with a band gap of 0.7 eV, determine the position of EF at T = 300 K if m*h = 6m*e.
A18)
Band gap 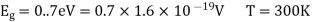
Fermi energy for an intrinsic semiconductor
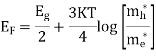
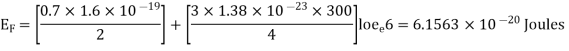

Fermi energy level 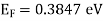
Q19) Find the resistance of an intrinsic Ge rod 1 mm long, 1 mm wide and 1 mm thick at 300 K. The intrinsic carrier density 2.5 ×1019 m–3 is at 300 K and the mobility of electron and hole are 0.39 and 0.19 m2 v–1 s–1.
A19)
Length of Ge rod 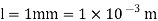
Breadth 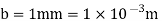
Thickness 
Intrinsic carrier concentration 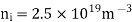
Mobility of electron 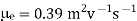
Mobility of hole 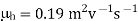
a) Conductivity

b) Resistance
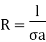

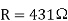
Q20) The intrinsic carrier density of a semiconductor is 2.1 × 1019 m–3. The electron and hole mobilities are 0.4 and 0.2 m2 V–1 s–1 respectively. Calculate the conductivity.
A20)
Intrinsic carrier concentration 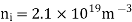
Mobility of electron 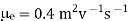
Mobility of hole 
Conductivity 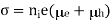
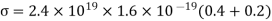
Conductivity 