Unit – 3
Trigonometric and exponential Fourier series
Q1) Three similar resistors are connected in star across 400V 3-phase lines. Line current is 4A. Calculate the value of each resistor.
A1) For star connection:
IL=Iph=4A
Vph=VL/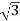 = 400/
= 400/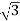 = 231V
= 231V
Rph= 231/4= 57.75ohm
For Delta Connection:
IL=4A
Iph= IL/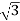
=4/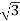 ==2.30A
==2.30A
Zph=400/2.30=173.9ohm
Rph= 173.9/3 = 57.97ohm
Q2) Three identical impedances are connected in delta 3-phase supply of 400V. The line current is 30A and total power taken from the supply is 10kW. Calculate the resistance and reactance value of each impedance?
A2) VL=Vph=400V
IL=30A
Iph=IL/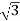 = 30/
= 30/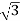 =17.32A
=17.32A
Zph=Vph/Iph= 400/17.32=23.09ohm
P=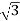 VLIL Cos Ø
VLIL Cos Ø
Cos Ø = 10000/ 400x30 = 0.48
400x30 = 0.48
Sin Ø =0.88
Rph=Zph Cos Ø= 23.09x0.48=11.08ohm
Xph=Zph Sin Ø = 23.09x0.88=20.32ohm
Q3) A star connected alternator supplies a delta connected load. The impedance of the load branch is 6+j5 ohm/phase. The line voltage is 230V. Determine the current in the load branch and power consumed by the load.
A3) Zph= = 7.8ohm
= 7.8ohm
VL=Vph=230V
Iph=Vph/Zph=230/7.8=29.49A
Iph=IL/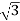
IL=  Iph=
Iph=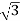 x29.49=51.07A
x29.49=51.07A
P=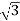 VLIL Cos Ø =
VLIL Cos Ø =  x 230x51.07x0.768=15.62kW
x 230x51.07x0.768=15.62kW
Q4) The load connected to a 3-phase supply comprise three similar coils connected in star. The line currents are 25A and the kVA and kW inputs are 18 and 10 respectively. Find the line and phase voltage, the kVAR input resistance and reactance of each coil?
A4) IL= 25A
P= 10000W
Cos Ø = 10/18 = 0.56
P=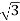 VLIL Cos Ø
VLIL Cos Ø
10000= x VLx25x0.56
x VLx25x0.56
VL =412.39V
Vph= VL/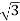 = 412.39/
= 412.39/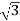 =238.09V
=238.09V
KVAR=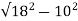 = 14.96
= 14.96
Zph=238.09/25=9.52ohm
Rph=Zph Cos Ø= 9.52x0.56=5.33ohm
Xph=Zph Sin Ø = 9.52x0.83=7.88ohm
Q5) A balanced delta connected load consisting of three coils draws 8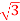 A at 0.5 p.f from 100V 3-phase ac supply. If the coils are reconnected in star across the same supply. Find the line current and total power consumed?
A at 0.5 p.f from 100V 3-phase ac supply. If the coils are reconnected in star across the same supply. Find the line current and total power consumed?
A5) For Delta connection:
IL=8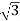 A
A
Iph= IL/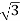 = 8A
= 8A
Vph=100V
Zph=100/8=12.5ohm
Rph=Zph Cos Ø=12.5x0.5 = 6.25ohm
Xph=Zph Sin Ø = 12.5x0.866=10.825ohm
P=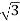 VLIL Cos Ø
VLIL Cos Ø
= 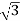 x 100x 8
x 100x 8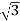 x0.5=1200W
x0.5=1200W
For Star Connection:
Vph= VL/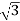 = 100/
= 100/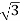 V=57.73V
V=57.73V
Zph=100/8=12.5ohm
Iph=57.73/12.5=4.62A
P=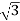 VLIL Cos Ø
VLIL Cos Ø
=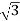 x 100x 4.62x0.5
x 100x 4.62x0.5
P= 400W
Q6) A 3-phase supply with a line voltage of 250V has an unbalanced delta connected load as shown in figure
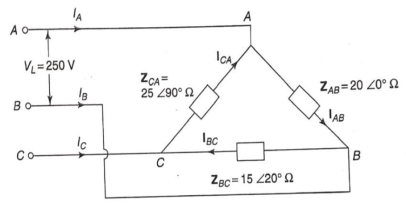
Find (a) Phase current (b) line current?
A6) From above figure we can write
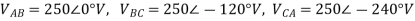
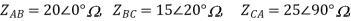
The phase currents are

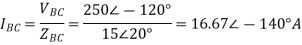

The Line currents are
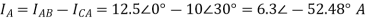
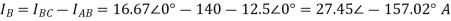
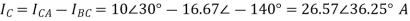
Q7) Find vc(t) for circuit shown in the figure?
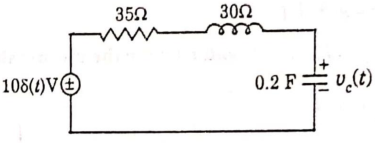
A7) Let the current in circuit be i(t). From KVL we have
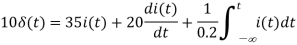
Taking F.T we get

As i(0+) =0 hence I(0)=0
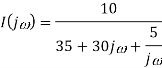

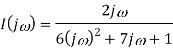
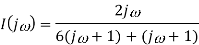
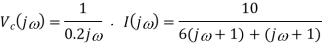
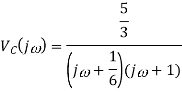
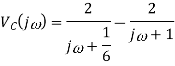
Takin IFT we get
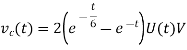
Q8) Find Fourier transform of the waveform given below?
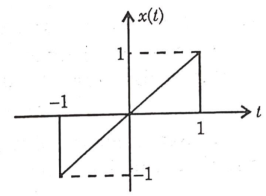
A8)
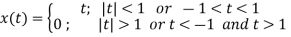
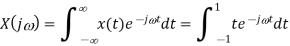
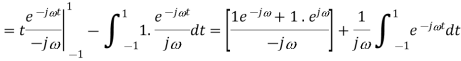

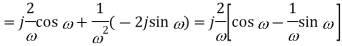
Q9) Find the Fourier series coefficients for the given saw tooth wave(in exponential form) as shown in figure
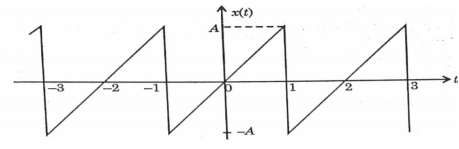
A9)
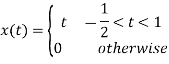
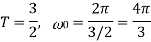
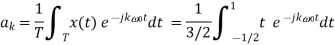
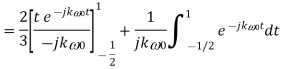
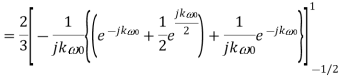
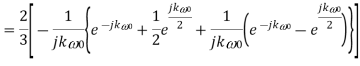
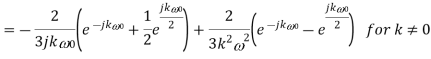
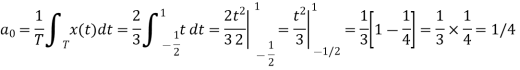

Q10) A continues time periodic signal x(t) has a fundamental period T=8. The nonzero Fourier series coefficients for x(t) are: 𝑎1 = 𝑎−1 = 2. 𝑎3 = 𝑎∗−3 = j4
Express x(t) in the form of
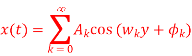
A10)
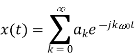
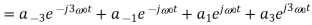
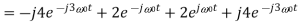

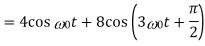
Here, 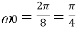
Therefore,
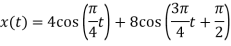
Q11) For the circuit shown in figure, Determine the voltage response 𝑣𝑜 𝑡 to a current source excitation i(t)=2𝑒−𝑡𝑢(𝑡), using Fourier transform?
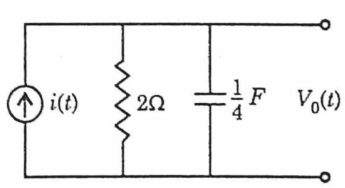
A11) We apply KCL
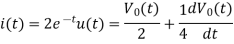
Taking FT of both sides we have

Therefore,
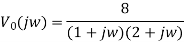
By partial fraction of above equation, we get
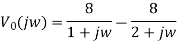
Taking IFT of above equation we get
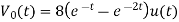
Q12) In the Circuit of fig., A 400 V, 50 Hz, three phase supply of phase sequence ABC is supplied to a delta connected load consisting of a 100 Ohm resistor between lines A and B, a 378 mH inductor between lines B and C, and a 37.8 micro farad capacitor between lines C and A. Determine Phase and line currents.
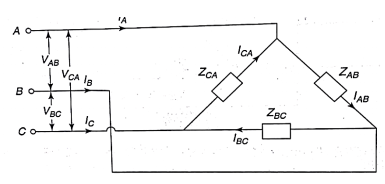
A12) VL = 400V, f=50Hz, R= 100 Ohm, L= 318mH, C=31.8 micro farad
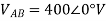
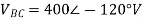
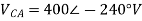
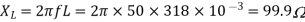
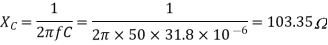
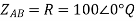

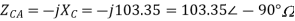
Phase Current
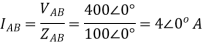
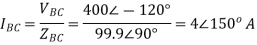
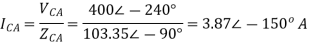
Line Currents
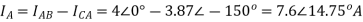
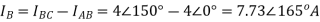
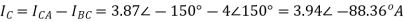
Q13) For a series RLC circuit having R=10ohms, L= 0.15H, C=100 F. They are connected across 100v 50Hz supply. Calculate total impedance?
F. They are connected across 100v 50Hz supply. Calculate total impedance?
A13) Impedance Z= 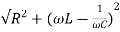
Z= 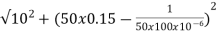 = 18.27ohm
= 18.27ohm
Q14) For a series RLC circuit having R=12ohms, L= 0.2H, C=60 F. They are connected across 100v 50Hz supply. Calculate circuit current?
F. They are connected across 100v 50Hz supply. Calculate circuit current?
A14) I= 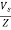
Z= 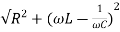
Z= 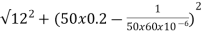 = 13.89ohm
= 13.89ohm
I = 100/13.89 =7.2A
Q15) For a series RLC circuit having R=10ohms, L= 0.15H, C=100 F. They are connected across 100v 50Hz supply. Calculate power factor?
F. They are connected across 100v 50Hz supply. Calculate power factor?
A15) cosφ = 
Impedance Z= 
Z= 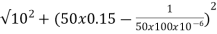 = 18.27ohm
= 18.27ohm
Cosφ =  =
= 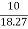
φ = 56.81o lagging
Q16) If V1=6cos2t, find i2 at steady state.
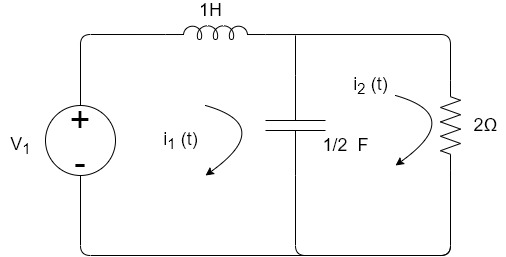
A16) Apply KVL
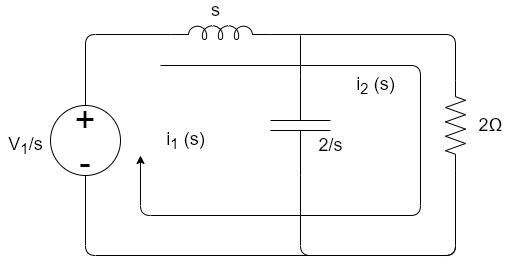
6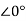 -sI1(s)-2I2(s)=0
-sI1(s)-2I2(s)=0
-2I2(s)-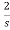 I2(s)+
I2(s)+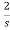 I1(s)=0
I1(s)=0
I2(s)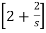 =
= I1(s)
I1(s)
I1(s)=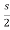 [
[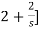 I2(s)
I2(s)
Substituting I1(s) in first equation
6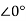 -s
-s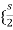 [
[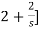 }I2(s)- 2I2(s)=0
}I2(s)- 2I2(s)=0
Solving above equation we get
I2(s)=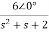
Replace s=jω, s=2j
I2(jω)=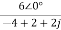 =
=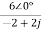 =
=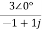
=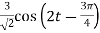
Q17) If V1=2sin2t, Va at steady state will be?
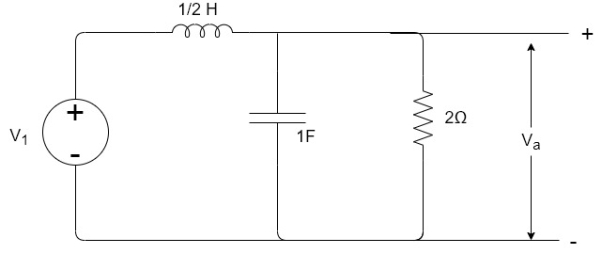
A17) Zeq=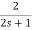
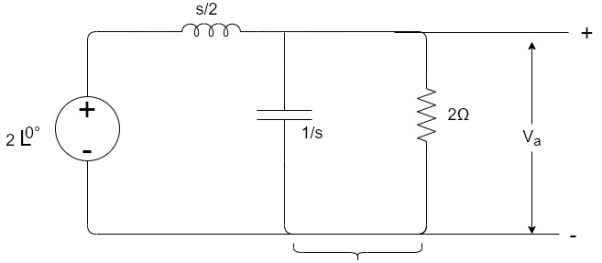
By voltage divider rule Va=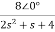
Replace s by jω , s=2j
Va= =
=
Va=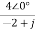 =
=
Va=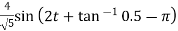
Q18) Find the Fourier integral of
f(x) = |sin x| |x| ≤ π
= 0 |x| ≥ π
Deduce that 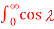 π +1/ 1 - 2 cos (π/2) d = π/2
π +1/ 1 - 2 cos (π/2) d = π/2
A18)
f(x) = 2/π 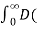
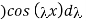
=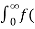 t
t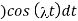 =
= 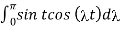
=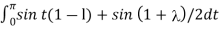
= - cost(1-) ]0 π - cost(1+) ]0 π
2(1-) 2(1+)
= 1/ 1- 2 [cos π+ 1]
=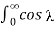 π +1/ 1 - 2 cos (π/2) d = π/2
π +1/ 1 - 2 cos (π/2) d = π/2
Q19) Find the Fourier Integral of
f(x) = 1 |x| ≤ 1
0 |x| ≥ 1
A19)
f(x) = 1/π 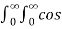 (t-x) dt d
(t-x) dt d
= 1/π 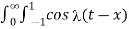 dt d
dt d
= 1/π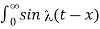 / ] -1 1 d
/ ] -1 1 d
= 1/π  -
- 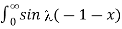 / d
/ d
= 1/π 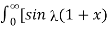 – sin
– sin 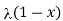 ]/ d
]/ d
= 2/π 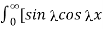 / d = π/2 when |x| < 1 and 0 when |x| >1
/ d = π/2 when |x| < 1 and 0 when |x| >1
By setting x=0
= 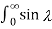 / d = π/2.
/ d = π/2.
Q20) Compute the Exponential series of the following series.
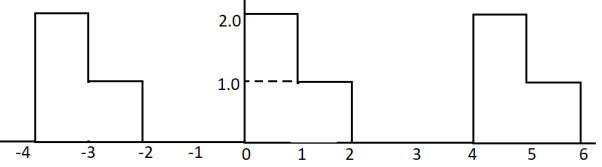
A20)
The time period of the signal x(t) is T=4.
Ω0 = 2π/T = 2 π/4= π/2
C0 = 1/T  = ¼ [
= ¼ [ +
+ 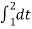
C0 = ¼ [ 2+1] = ¾
Cn = 1/T [ 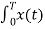 e-jnΩot dt = ¼[
e-jnΩot dt = ¼[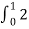 e-jnπ/2t dt +
e-jnπ/2t dt + 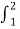 e-jn π/2t dt
e-jn π/2t dt
= ½. 1/ -jn π/2 [e-jn π/2t ] 0 1 + ¼ 1/-jn π/2[ e-jn π/2t ] 1 2
= - 1/jn π[e-jn π/2 – 1] – 1/ 2jn π (e-jn π – e-jn π/2 )
= 1/jn π[ 1 - e-jn π/2 ] – 1/ 2 e-jn π + ½ e-jn π/2 )
= 1/jn π [ 1- ½ (-1) n -1/2 e-j n π/2 ]