UNIT 1
Review of signals and systems
1. Check whether the systems are linear or not.
a)dy/dt + 3t y(t) = t2 x(t)
b) y(t) =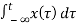 
c) y(n) = Ax(n) + B
Solution:
a) dy/dt + 3t y(t) = t2 x(t)
For input x1(t) the output is y1(t)
dy1(t)/dt + 3t y1(t) = t2 x1(t) --------- (1)
Similarly, for x2(t) output is y2(t)
dy2(t)/dt + 3t y2(t) = t2 x2(t) ---------- (2)
Multiply (1) with a and (2) with b
a dy1(t) /dt + 3at y1(t) + b dy2(t)/dt + 3by2(t) = at2 x1(t) + bt2 x2(t)
d/dt[ay1(t) +by2(t)] + 3t[ay1(t) + by2(t)] = t2[ax1(t) + bx2(t)]
The system is linear because weighted sum of inputs produces the corresponding weighted sum of outputs.
b) y(t) =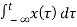 
For x1 input output is y1(t)
y1(t) =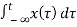
y2((t)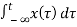 
Linear combination of both yields
ay1(t) + by2(t) = a 
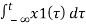+ b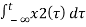 
= 
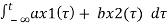
Linear combination of inputs
Linear combination of outputs
Therefore, system is linear.
c) y(n) = Ax(n) + B
For input x1(n) the corresponding output is y1(n)
y1(n) = T[x1(n)] = Ax1(n) + B ; y2(n) = Tx2(n)] = A x2(n) + B
Ay1(n) + by2(n) = a[Ax1(n) + B] + b[Ax2(n) +B]
The output will be y3(n) = A[x1(n) + x2(n) ] +B
y3(n) ≠ ay1(n) + by2(n)
Therefore, system is non-linear.
2. Determine whether the following systems are time variant or time invariant.
a) y(t) = x(t) cos 50πt
b) y(t) = e x(t)
c) y(t) = x(t2)
d) y(n) = x2(n-1)
a)y(t) = x(t) cos 50πt
If the input is delayed by T sec then output
y(t,T) = T[x(t-T)] = x(t-T) cos (50πt)
If the output is delayed by T sec then
y(t-T) = x(t-T) cos 50 π(t –T)
y(t,T) ≠ y(t – T)
Hence the system is time-variant.
b)y(t) = ex(t)
The output for delayed input is
y(t,T) = e x(t-T)
The delayed output is
y(t-T) = ex(t-T)
y(t,T) = y(t-T)
Hence, system is time-invariant.
c)y(t) = x(t2)
The output for delayed input is
y(t,T) = x(t2 –T)
The delayed output is
y(t-T) = x(t-T)2
y(t,T) ≠ y(t – T)
Hence the system is time variant
d)y(n) = x2 (n-1)
The output for delayed input is
y(n-k) = x2(n-1-k)
The delayed output is
y(n-k) = x2 (n-1-k)
y(n,k) = y(n-k)
System is time invariant.
3. If y(t) = 2 x(t) + 3 x(t-3) then check whether it is causal or non-causal.
Let t=1 therefore y(1) = 2 x(1) + 3 x(-2)
The system output only depends upon present and past inputs. Hence, the system is causal.
y(t) = 2 x(t) + 3 x(t – 3) + 6 x( t+3)
Let t=1 the system output is
y(1) = 2x(1) + 3 x(-2) + 6 x( 4)
Here the output depends future input. Hence non –casual.
4. Check whether the following systems are
Static or dynamic
Linear or Non-linear
Causal or non-casual
Time Invariant or time variant
a) y(t) d2y(t) /dt2 + 3t dy(t)/dt + y(t) = x(t)
- Since it is a differential equation the system is dynamic.
- The input x1(t) and output y1(t) can be described by
y1(t) d2 y1(t)/dt2 + 3t dy1(t)/dt + y1(t) = x1(t)
Similarly, y2(t) d2y2(t)/dt2 + 3t dy2(t)/dt + y2(t) =x2(t)
a y1(t) d2y1(t)/dt2 + 3at dy1(t)/dt + a y1(t) + b y2(t) d2y1(t)/dt2 + 3bt dy1(t)/dt +by2(t) = ax1(t) + b x2(t)
Ay1 d2 y1(t)/dt2 + by2(t) d2 y(t)/dt2 + 3t d/dt[ay1(t) + b2 y2(t)] + ay1(t) + b y2(t) = ax1(t) + bx2(t)
Since the differentiation ay1(t) d2 y1(t)/dt2 + by2(t) d2 y2(t)/dt2 is not a function of the weighted sum of outputs, superposition principle is not satisfied hence the system is non-linear.
- The output depends on the present input only hence the system is causal.
- The co-efficient of the differential equations are function of time. Hence the system is time-variant.
b) y(n) = x(n) x(n-1)
The output depends the past values of input . Hence it requires memory therefore the system is dynamic.
The output y1(n) for input x1(n) is
y1(n) = x1(n) x1(n-1)
y2(n) = x2(n) x2(n-1)
y3(n) = ax1(n) + b x2(n) [ax1(n-1)+ b x2(n-1)]
a y1(n) + by2(n) = a x1(n) x1(n-1) + bx2(n) x2(n-1)
Since y3(n) ≠ ay1(n) + b y2(n)
Hence the system is non-linear.
The output depends on the present and past values of input .Hence the system is casual.
y(n) = x(n) x(n-1)
y(n,k) = x(n-k) x(n-1-k)
y(n-k) = x(n-k) x(n-1-k)
Since y(n,k) = y(n-k) the system is time-invariant.
c) y (n) = cos[x(n)]
The output depends on the input at that instant. Therefore, system is static.
For input x1(n)
y1(n ) = cos[x1(n)]
For input x2(n)
y2(n) = cos[x2(n)]
y3(n) = cos[ax1(n) + b x2(n)]
a y1(n) + b y2(n) = a cos [x1(n)] + b cos[x2(n)]
Hence the system is non-linear.
The output depends on the present input hence the system is casual.
y(n) = cos[x(n)]
y(n,k) = cos[x(n-k)]
y(n-k) = cos[x(n-k)]
y(n,k) = y(n-k)
Hence system is time –invariant.
For the given system check whether the system is linear, time-invariant ,casual memoryless or stable.
Y(t) = x(t-2)+ x(2-t)
- System is not memoryless since the output depends on the past and future values of input.
- The system is non-casual since output depends on the future values of input.
y(t,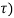
= x1(t-2-
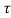)+x1(2-t-
)
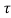y(t-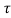
) = x(t-2-
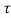) + x2(2-t+
)
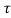y(t,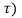
≠ y(t-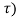
System is time variant.
y1(t) = x1(t-2) + x1(2-t)
y2(t) = x2(t-2) + x2(2-t)
a1y1(t) + a2 y2(t) = a1 x1(t-2)+ a1x1(2-t) + a2x2(t-2)+a2x2(2-t)
= a1x1(t-2) + ax2(t-2) +a1x1(2-t)+a2 x2(2-t)
= System is linear.
For bounded input , the output is also bounded. Hence the system is stable.
5. Evaluate the following integrals:
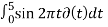
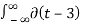(t-3) 2 dt
Solution:
1) 
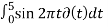
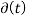= 1 for t=0. For t≠ 0 =0.
= 
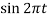|t=0 = 0
2) 
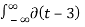(t-3) 2 dt for t=3 
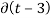= 1
(t-3) 2 |t=3 =0
6. If Ac = 5V, Am = 2V. Find m, Pt ?
M = Am / Ac = 2 / 5 = 0.4
Pc = Ac2 / 2 = 25 / 2 = 12.5 watt
PLSB = PUSB = m2 Ac2 / 8 = ( 0.4 )2 25 / 8
= 0.5 watt
Pt = Pc + PLSB + PUSB
= 12.5 + 0.5 + 0.5
= 35.5 watt
P= m2 / 2 + m2 = ( 0.4 )2 / 2 + ( 0.4 )2
= 0.16 / 2 + 0.16
= 0.074 = 7.4 %
7. Explain SSB with its generation techniques.
SSB – SC has only one sideband to be transmitted hence there is significant reduction of power and bandwidth.
SSBSC technique has following disadvantages.
1>. The receiver for SSB – SC is more complex because of the absence of carrier and another sideband.
2>. Practically it is not easy to suppress the other sideband as it is very close to the sideband which has to be retained.
Methods of Generation of SSB – SC signal: -
There are mainly two methods of generation of SSB – SC modulated signals.
1>. Filter method or Balance modulator filter method
In this method we first generate a DSB – SC signal and then filter out the unwanted sideband.
2>. Phasing method
3>. Variant of phasing method named weaver’s method
4>. Third method having advantages of filter and phase shift method.
8. Explain VSB.
Vestigial sideband (VSB) modulation is used in T.V. Signal since AM & SSB – SC is not suitable.
In VSB carrier one sideband and part of another sideband (vestige) is also transmitted.
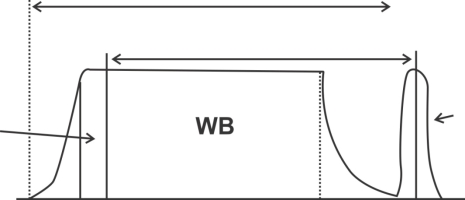
Fig.: Vestigial Band
The VSB modulation is used for modulating video (picture) signal only. Thus, above figure clearly indicate that if AM is used for video signal the bandwidth will become 11.25 MHz using VSB modulation technique a part of LSB is taken & hence the bandwidth of one channel becomes 7 MHz.
UNIT 1
Review of signals and systems
1. Check whether the systems are linear or not.
a)dy/dt + 3t y(t) = t2 x(t)
b) y(t) =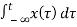 
c) y(n) = Ax(n) + B
Solution:
a) dy/dt + 3t y(t) = t2 x(t)
For input x1(t) the output is y1(t)
dy1(t)/dt + 3t y1(t) = t2 x1(t) --------- (1)
Similarly, for x2(t) output is y2(t)
dy2(t)/dt + 3t y2(t) = t2 x2(t) ---------- (2)
Multiply (1) with a and (2) with b
a dy1(t) /dt + 3at y1(t) + b dy2(t)/dt + 3by2(t) = at2 x1(t) + bt2 x2(t)
d/dt[ay1(t) +by2(t)] + 3t[ay1(t) + by2(t)] = t2[ax1(t) + bx2(t)]
The system is linear because weighted sum of inputs produces the corresponding weighted sum of outputs.
b) y(t) =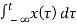 
For x1 input output is y1(t)
y1(t) =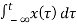
y2((t)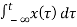 
Linear combination of both yields
ay1(t) + by2(t) = a 
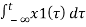+ b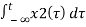 
= 
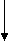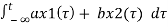
Linear combination of inputs
Linear combination of outputs
Therefore, system is linear.
c) y(n) = Ax(n) + B
For input x1(n) the corresponding output is y1(n)
y1(n) = T[x1(n)] = Ax1(n) + B ; y2(n) = Tx2(n)] = A x2(n) + B
Ay1(n) + by2(n) = a[Ax1(n) + B] + b[Ax2(n) +B]
The output will be y3(n) = A[x1(n) + x2(n) ] +B
y3(n) ≠ ay1(n) + by2(n)
Therefore, system is non-linear.
2. Determine whether the following systems are time variant or time invariant.
a) y(t) = x(t) cos 50πt
b) y(t) = e x(t)
c) y(t) = x(t2)
d) y(n) = x2(n-1)
a)y(t) = x(t) cos 50πt
If the input is delayed by T sec then output
y(t,T) = T[x(t-T)] = x(t-T) cos (50πt)
If the output is delayed by T sec then
y(t-T) = x(t-T) cos 50 π(t –T)
y(t,T) ≠ y(t – T)
Hence the system is time-variant.
b)y(t) = ex(t)
The output for delayed input is
y(t,T) = e x(t-T)
The delayed output is
y(t-T) = ex(t-T)
y(t,T) = y(t-T)
Hence, system is time-invariant.
c)y(t) = x(t2)
The output for delayed input is
y(t,T) = x(t2 –T)
The delayed output is
y(t-T) = x(t-T)2
y(t,T) ≠ y(t – T)
Hence the system is time variant
d)y(n) = x2 (n-1)
The output for delayed input is
y(n-k) = x2(n-1-k)
The delayed output is
y(n-k) = x2 (n-1-k)
y(n,k) = y(n-k)
System is time invariant.
3. If y(t) = 2 x(t) + 3 x(t-3) then check whether it is causal or non-causal.
Let t=1 therefore y(1) = 2 x(1) + 3 x(-2)
The system output only depends upon present and past inputs. Hence, the system is causal.
y(t) = 2 x(t) + 3 x(t – 3) + 6 x( t+3)
Let t=1 the system output is
y(1) = 2x(1) + 3 x(-2) + 6 x( 4)
Here the output depends future input. Hence non –casual.
4. Check whether the following systems are
Static or dynamic
Linear or Non-linear
Causal or non-casual
Time Invariant or time variant
a) y(t) d2y(t) /dt2 + 3t dy(t)/dt + y(t) = x(t)
- Since it is a differential equation the system is dynamic.
- The input x1(t) and output y1(t) can be described by
y1(t) d2 y1(t)/dt2 + 3t dy1(t)/dt + y1(t) = x1(t)
Similarly, y2(t) d2y2(t)/dt2 + 3t dy2(t)/dt + y2(t) =x2(t)
a y1(t) d2y1(t)/dt2 + 3at dy1(t)/dt + a y1(t) + b y2(t) d2y1(t)/dt2 + 3bt dy1(t)/dt +by2(t) = ax1(t) + b x2(t)
Ay1 d2 y1(t)/dt2 + by2(t) d2 y(t)/dt2 + 3t d/dt[ay1(t) + b2 y2(t)] + ay1(t) + b y2(t) = ax1(t) + bx2(t)
Since the differentiation ay1(t) d2 y1(t)/dt2 + by2(t) d2 y2(t)/dt2 is not a function of the weighted sum of outputs, superposition principle is not satisfied hence the system is non-linear.
- The output depends on the present input only hence the system is causal.
- The co-efficient of the differential equations are function of time. Hence the system is time-variant.
b) y(n) = x(n) x(n-1)
The output depends the past values of input . Hence it requires memory therefore the system is dynamic.
The output y1(n) for input x1(n) is
y1(n) = x1(n) x1(n-1)
y2(n) = x2(n) x2(n-1)
y3(n) = ax1(n) + b x2(n) [ax1(n-1)+ b x2(n-1)]
a y1(n) + by2(n) = a x1(n) x1(n-1) + bx2(n) x2(n-1)
Since y3(n) ≠ ay1(n) + b y2(n)
Hence the system is non-linear.
The output depends on the present and past values of input .Hence the system is casual.
y(n) = x(n) x(n-1)
y(n,k) = x(n-k) x(n-1-k)
y(n-k) = x(n-k) x(n-1-k)
Since y(n,k) = y(n-k) the system is time-invariant.
c) y (n) = cos[x(n)]
The output depends on the input at that instant. Therefore, system is static.
For input x1(n)
y1(n ) = cos[x1(n)]
For input x2(n)
y2(n) = cos[x2(n)]
y3(n) = cos[ax1(n) + b x2(n)]
a y1(n) + b y2(n) = a cos [x1(n)] + b cos[x2(n)]
Hence the system is non-linear.
The output depends on the present input hence the system is casual.
y(n) = cos[x(n)]
y(n,k) = cos[x(n-k)]
y(n-k) = cos[x(n-k)]
y(n,k) = y(n-k)
Hence system is time –invariant.
For the given system check whether the system is linear, time-invariant ,casual memoryless or stable.
Y(t) = x(t-2)+ x(2-t)
- System is not memoryless since the output depends on the past and future values of input.
- The system is non-casual since output depends on the future values of input.
y(t,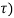
= x1(t-2-
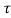)+x1(2-t-
)
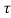y(t-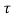
) = x(t-2-
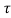) + x2(2-t+
)
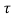y(t,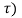
≠ y(t-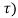
System is time variant.
y1(t) = x1(t-2) + x1(2-t)
y2(t) = x2(t-2) + x2(2-t)
a1y1(t) + a2 y2(t) = a1 x1(t-2)+ a1x1(2-t) + a2x2(t-2)+a2x2(2-t)
= a1x1(t-2) + ax2(t-2) +a1x1(2-t)+a2 x2(2-t)
= System is linear.
For bounded input , the output is also bounded. Hence the system is stable.
5. Evaluate the following integrals:
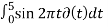
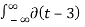(t-3) 2 dt
Solution:
1) 
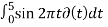
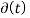= 1 for t=0. For t≠ 0 =0.
= 
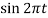|t=0 = 0
2) 
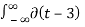(t-3) 2 dt for t=3 
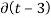= 1
(t-3) 2 |t=3 =0
6. If Ac = 5V, Am = 2V. Find m, Pt ?
M = Am / Ac = 2 / 5 = 0.4
Pc = Ac2 / 2 = 25 / 2 = 12.5 watt
PLSB = PUSB = m2 Ac2 / 8 = ( 0.4 )2 25 / 8
= 0.5 watt
Pt = Pc + PLSB + PUSB
= 12.5 + 0.5 + 0.5
= 35.5 watt
P= m2 / 2 + m2 = ( 0.4 )2 / 2 + ( 0.4 )2
= 0.16 / 2 + 0.16
= 0.074 = 7.4 %
7. Explain SSB with its generation techniques.
SSB – SC has only one sideband to be transmitted hence there is significant reduction of power and bandwidth.
SSBSC technique has following disadvantages.
1>. The receiver for SSB – SC is more complex because of the absence of carrier and another sideband.
2>. Practically it is not easy to suppress the other sideband as it is very close to the sideband which has to be retained.
Methods of Generation of SSB – SC signal: -
There are mainly two methods of generation of SSB – SC modulated signals.
1>. Filter method or Balance modulator filter method
In this method we first generate a DSB – SC signal and then filter out the unwanted sideband.
2>. Phasing method
3>. Variant of phasing method named weaver’s method
4>. Third method having advantages of filter and phase shift method.
8. Explain VSB.
Vestigial sideband (VSB) modulation is used in T.V. Signal since AM & SSB – SC is not suitable.
In VSB carrier one sideband and part of another sideband (vestige) is also transmitted.
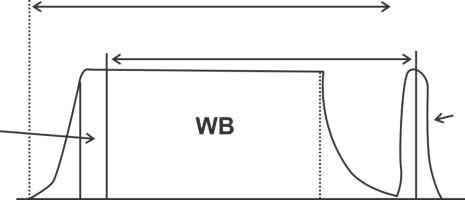
Fig.: Vestigial Band
The VSB modulation is used for modulating video (picture) signal only. Thus, above figure clearly indicate that if AM is used for video signal the bandwidth will become 11.25 MHz using VSB modulation technique a part of LSB is taken & hence the bandwidth of one channel becomes 7 MHz.
