UNIT 4

Pulse and Delta Modulation

1. Define Pulse modulation.

Here, the signal is transmitted in the form of pulses. It can be used to transmit analogue information. In pulse modulation, continuous signals are sampled at regular intervals.

Pulse modulation can be classified into two major types.

• Analogue: Indication of sample amplitude is infinitely variable
• Digital: Indicates sample amplitude at the nearest predetermined level.

2.     Define Sampling rate, Sampling Frequency, Nyquist Rate.

Sampling Rate

To discretize the signals, the gap between the samples should be fixed. That gap can be termed as a sampling period Ts.

Sampling Frequency=1/Ts=fs

Where,

• Ts is the sampling time
• Fs is the sampling frequency or the sampling rate

Sampling Frequency

Sampling frequency is the reciprocal of the sampling period. This sampling frequency, can be simply called as Sampling rate. The sampling rate denotes the number of samples taken per second, or for a finite set of values.

Nyquist Rate

Suppose that a signal is band-limited with no frequency components higher than W Hertz. That means, W is the highest frequency. For such a signal, for effective reproduction of the original signal, the sampling rate should be twice the highest frequency.

Which means,

fS=2W

Where,

• fS is the sampling rate
• W is the highest frequency

This rate of sampling is called as Nyquist rate.

3.     State Sampling theorem.

The sampling theorem, which is also called as Nyquist theorem, delivers the theory of sufficient sample rate in terms of bandwidth for the class of functions that are bandlimited.

The sampling theorem states that, “a signal can be exactly reproduced if it is sampled at the rate fs which is greater than twice the maximum frequency W.”

Let us consider a band-limited signal, i.e., a signal whose value is non-zero between some –W and W Hertz.

Such a signal is represented as x(f)=0 for ∣f∣>W

For the continuous-time signal x (t), the band-limited signal in frequency domain, can be represented as shown in the following figure.

                                    Fig.: Band limited signal

If the signal x(t) is sampled above the Nyquist rate, the original signal can be recovered, and if it is sampled below the Nyquist rate, the signal cannot be recovered.

The following figure explains a signal, if sampled at a higher rate than 2w in the frequency domain.

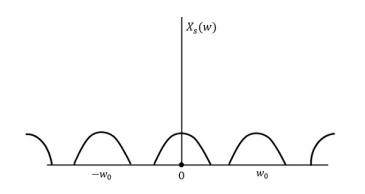
                                    Fig.: Sampled at a higher rate than 2w

The above figure shows the Fourier transform of a signal xs (t).

If fs<2W

The resultant pattern will look like the following figure.

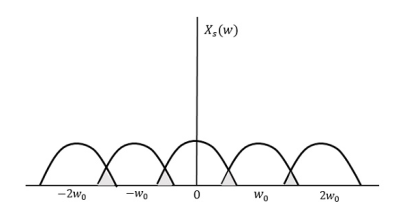
                                                 Fig.: Resultant pattern

Here, the over-lapping of information is done, which leads to mixing up and loss of information. This unwanted phenomenon of over-lapping is called as Aliasing.

4.     What is PAM? Explain.

It is the simplest form of Pulse Modulation. In this type of modulation, each sample is made proportional to the amplitude of the signal at the instant of sampling. The PAM signal follows the amplitude of the original signal, as the signal traces out the path of the whole wave. Here a signal which is sampled at Nyquist rate can be reconstructed by passing it through an efficient Low Pass Filter (LPF) with exact cutoff frequency. It is very easy to generate and demodulate PAM. This technique transmits the data by encoding in the amplitude of a series of signal pulses.

There are two types of PAM.

1. Single Polarity PAM: A fixed DC level is added to the signal so that the signal is always positive.
2. Double Polarity PAM: Here the pulses are both positive and negative.

                                                            Fig. : PAM

5.     Explain PCM using block diagram.

• Pulse code modulation is a method that is used to convert an analog signal into a digital signal, so that modified analog signal can be transmitted through the digital communication network.
• PCM is in binary form, so there will be only two possible states high and low(0 and 1).
• The Pulse Code Modulation process is done in three steps Sampling, Quantization, and Coding.
• There are two specific types of pulse code modulations such as differential pulse code modulation (DPCM) and adaptive differential pulse code modulation (ADPCM)

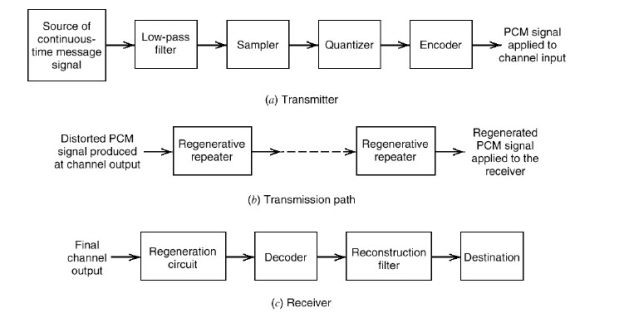
                                                            Fig. : PCM

To get the pulse code modulated waveform from an analog wave form at the transmitter end(source) of a communication circuit the amplitude of the analog signal samples at regular time intervals. The sampling rate or the number of samples per second is several times the maximum frequency.

The message signal is converted into binary form which is in the number of levels always to the power of 2. This process is called quantization.

At the receiver end, pulse code demodulator decodes the binary signal back into pulses with same quantum levels as those in the modulator.

6.     Explain differential PCM.

DPCM Transmitter

The DPCM Transmitter consists of Quantizer and Predictor with two summer circuits.

Following is the block diagram of DPCM transmitter.

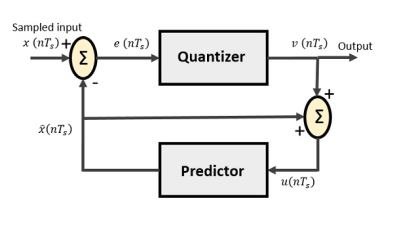                                                                                                            Fig. : DPCM

The signals at each point are named as −

• x(nTs) is the sampled input
• xˆ(nTs) is the predicted sample
• e(nTs) is the difference of sampled input and predicted output, often called as prediction error
• v(nTs) is the quantized output
• u(nTs) is the predictor input which is actually the summer output of the predictor output and the quantizer output

The predictor produces the assumed samples from the previous outputs of the transmitter circuit. The input to this predictor is the quantized versions of the input signal x(nTs).

Quantizer Output is represented as −

v(nTs)=Q[e(nTs)]

=e(nTs)+q(nTs)

Where q (nTs) is the quantization error

Predictor input is the sum of quantizer output and predictor output,

u(nTs)=xˆ(nTs)+v(nTs)

u(nTs)=xˆ(nTs)+e(nTs)+q(nTs)

u(nTs)=x(nTs)+q(nTs)

The same predictor circuit is used in the decoder to reconstruct the original input.

DPCM Receiver

The block diagram of DPCM Receiver consists of a decoder, a predictor, and a summer circuit. Following is the diagram of DPCM Receiver.

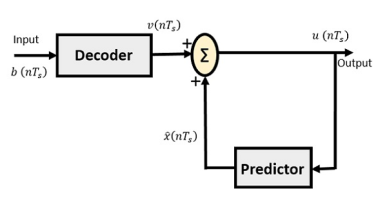
                                                            Fig. : DPCM Receiver

The notation of the signals is the same as the previous ones. In the absence of noise, the encoded receiver input will be the same as the encoded transmitter output.

As mentioned before, the predictor assumes a value, based on the previous outputs. The input given to the decoder is processed and that output is summed up with the output of the predictor, to obtain a better output.

7.     Explain digital multiplexing in detail.

The term digital represents the discrete bits of information. Hence, the available data is in the form of frames or packets, which are discrete.

Time Division Multiplexing (TDM)

In TDM, the time frame is divided into slots. This technique is used to transmit a signal over a single communication channel, by allotting one slot for each message.

Of all the types of TDM, the main ones are Synchronous and Asynchronous TDM.

Synchronous TDM

In Synchronous TDM, the input is connected to a frame. If there are ‘n’ number of connections, then the frame is divided into ‘n’ time slots. One slot is allocated for each input line.

In this technique, the sampling rate is common for all signals and hence the same clock input is given. The MUX allocates the same slot to each device at all times.

Asynchronous TDM

In Asynchronous TDM, the sampling rate is different for each of the signals and a common clock is not required. If the allotted device, for a time slot transmits nothing and sits idle, then that slot is allotted to another device, unlike synchronous.

8.     What are the advantages of DM Over DPCM.

• 1-bit quantizer
• Very easy design of the modulator and the demodulator

However, there exists some noise in DM.

• Slope Over load distortion (when Δ is small)
• Granular noise (when Δ is large)

9.     Write the features and describe delta modulator.

The Delta Modulator comprises of a 1-bit quantizer and a delay circuit along with two summer circuits. Following is the block diagram of a delta modulator.

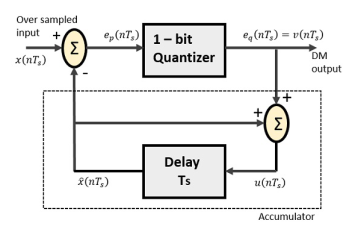
                                                            Fig. : Delta modulation

The predictor circuit in DPCM is replaced by a simple delay circuit in DM.

From the above diagram, we have the notations as −

• x(nTs)= over sampled input
• Ep(nTs) = summer output and quantizer input
• Eq(nTs) = quantizer output = v(nTs)
• xˆ(nTs) = output of delay circuit
• u(nTs) = input of delay circuit

Using these notations, now we shall try to figure out the process of delta modulation.

Ep(nTs)=x(nTs)−xˆ(nTs)           ---------equation 1

=x(nTs)−u([n−1]Ts

=x(nTs)−[xˆ[[n−1]Ts]+v[[n−1]Ts]]  -------equation 2

Further,

v(nTs)=eq(nTs)=S.sig.[ep(nTs)]   ---------equation 3

u(nTs)=xˆ(nTs)+eq(nTs)

Where,

• xˆ(nTs) = the previous value of the delay circuit
• Eq(nTs) = quantizer output = v(nTs)

Hence,

u(nTs)=u([n−1]Ts)+v(nTs)       ---------equation 4

Which means,

The present input of the delay unit

= The previous output of the delay unit + the present quantizer output the present quantizer output

Assuming zero condition of Accumulation,

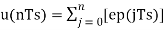
Accumulated version of DM output = 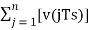         --------equation 5

Now, note that

xˆ(nTs)=u([n−1]Ts)

=---------equation 6

Delay unit output is an Accumulator output lagging by one sample.

From equations 5 & 6, we get a possible structure for the demodulator.

A Stair-case approximated waveform will be the output of the delta modulator with the step-size as delta (Δ). The output quality of the waveform is moderate.

UNIT 4

UNIT 4

Pulse and Delta Modulation

1. Define Pulse modulation.

Here, the signal is transmitted in the form of pulses. It can be used to transmit analogue information. In pulse modulation, continuous signals are sampled at regular intervals.

Pulse modulation can be classified into two major types.

• Analogue: Indication of sample amplitude is infinitely variable
• Digital: Indicates sample amplitude at the nearest predetermined level.

2.     Define Sampling rate, Sampling Frequency, Nyquist Rate.

Sampling Rate

To discretize the signals, the gap between the samples should be fixed. That gap can be termed as a sampling period Ts.

Sampling Frequency=1/Ts=fs

Where,

• Ts is the sampling time
• Fs is the sampling frequency or the sampling rate

Sampling Frequency

Sampling frequency is the reciprocal of the sampling period. This sampling frequency, can be simply called as Sampling rate. The sampling rate denotes the number of samples taken per second, or for a finite set of values.

Nyquist Rate

Suppose that a signal is band-limited with no frequency components higher than W Hertz. That means, W is the highest frequency. For such a signal, for effective reproduction of the original signal, the sampling rate should be twice the highest frequency.

Which means,

fS=2W

Where,

• fS is the sampling rate
• W is the highest frequency

This rate of sampling is called as Nyquist rate.

3.     State Sampling theorem.

The sampling theorem, which is also called as Nyquist theorem, delivers the theory of sufficient sample rate in terms of bandwidth for the class of functions that are bandlimited.

The sampling theorem states that, “a signal can be exactly reproduced if it is sampled at the rate fs which is greater than twice the maximum frequency W.”

Let us consider a band-limited signal, i.e., a signal whose value is non-zero between some –W and W Hertz.

Such a signal is represented as x(f)=0 for ∣f∣>W

For the continuous-time signal x (t), the band-limited signal in frequency domain, can be represented as shown in the following figure.

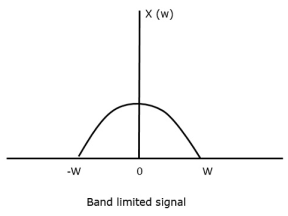
                                    Fig.: Band limited signal

If the signal x(t) is sampled above the Nyquist rate, the original signal can be recovered, and if it is sampled below the Nyquist rate, the signal cannot be recovered.

The following figure explains a signal, if sampled at a higher rate than 2w in the frequency domain.

                                    Fig.: Sampled at a higher rate than 2w

The above figure shows the Fourier transform of a signal xs (t).

If fs<2W

The resultant pattern will look like the following figure.

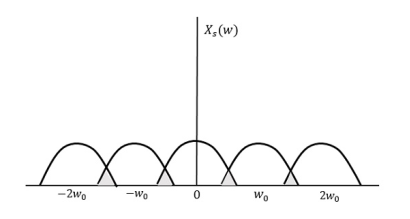
                                                 Fig.: Resultant pattern

Here, the over-lapping of information is done, which leads to mixing up and loss of information. This unwanted phenomenon of over-lapping is called as Aliasing.

4.     What is PAM? Explain.

It is the simplest form of Pulse Modulation. In this type of modulation, each sample is made proportional to the amplitude of the signal at the instant of sampling. The PAM signal follows the amplitude of the original signal, as the signal traces out the path of the whole wave. Here a signal which is sampled at Nyquist rate can be reconstructed by passing it through an efficient Low Pass Filter (LPF) with exact cutoff frequency. It is very easy to generate and demodulate PAM. This technique transmits the data by encoding in the amplitude of a series of signal pulses.

There are two types of PAM.

1. Single Polarity PAM: A fixed DC level is added to the signal so that the signal is always positive.
2. Double Polarity PAM: Here the pulses are both positive and negative.

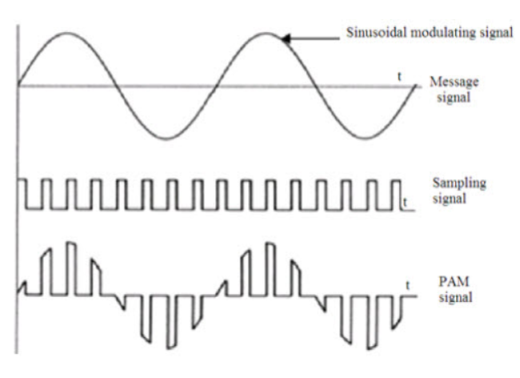
                                                            Fig. : PAM

5.     Explain PCM using block diagram.

• Pulse code modulation is a method that is used to convert an analog signal into a digital signal, so that modified analog signal can be transmitted through the digital communication network.
• PCM is in binary form, so there will be only two possible states high and low(0 and 1).
• The Pulse Code Modulation process is done in three steps Sampling, Quantization, and Coding.
• There are two specific types of pulse code modulations such as differential pulse code modulation (DPCM) and adaptive differential pulse code modulation (ADPCM)

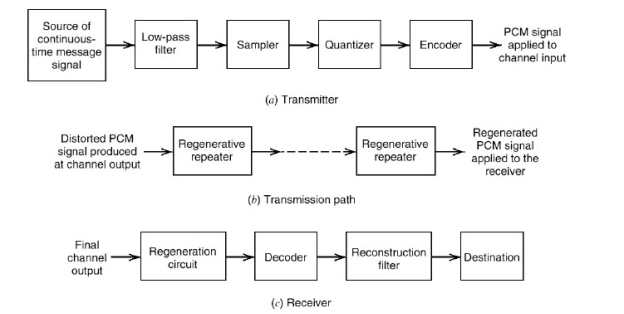
                                                            Fig. : PCM

To get the pulse code modulated waveform from an analog wave form at the transmitter end(source) of a communication circuit the amplitude of the analog signal samples at regular time intervals. The sampling rate or the number of samples per second is several times the maximum frequency.

The message signal is converted into binary form which is in the number of levels always to the power of 2. This process is called quantization.

At the receiver end, pulse code demodulator decodes the binary signal back into pulses with same quantum levels as those in the modulator.

6.     Explain differential PCM.

DPCM Transmitter

The DPCM Transmitter consists of Quantizer and Predictor with two summer circuits.

Following is the block diagram of DPCM transmitter.

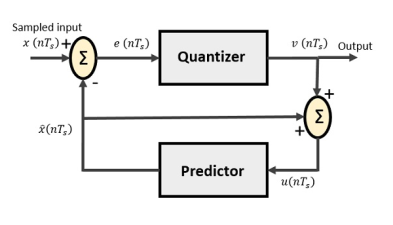                                                                                                            Fig. : DPCM

The signals at each point are named as −

• x(nTs) is the sampled input
• xˆ(nTs) is the predicted sample
• e(nTs) is the difference of sampled input and predicted output, often called as prediction error
• v(nTs) is the quantized output
• u(nTs) is the predictor input which is actually the summer output of the predictor output and the quantizer output

The predictor produces the assumed samples from the previous outputs of the transmitter circuit. The input to this predictor is the quantized versions of the input signal x(nTs).

Quantizer Output is represented as −

v(nTs)=Q[e(nTs)]

=e(nTs)+q(nTs)

Where q (nTs) is the quantization error

Predictor input is the sum of quantizer output and predictor output,

u(nTs)=xˆ(nTs)+v(nTs)

u(nTs)=xˆ(nTs)+e(nTs)+q(nTs)

u(nTs)=x(nTs)+q(nTs)

The same predictor circuit is used in the decoder to reconstruct the original input.

DPCM Receiver

The block diagram of DPCM Receiver consists of a decoder, a predictor, and a summer circuit. Following is the diagram of DPCM Receiver.

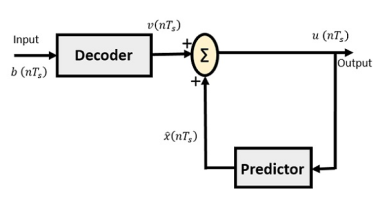
                                                            Fig. : DPCM Receiver

The notation of the signals is the same as the previous ones. In the absence of noise, the encoded receiver input will be the same as the encoded transmitter output.

As mentioned before, the predictor assumes a value, based on the previous outputs. The input given to the decoder is processed and that output is summed up with the output of the predictor, to obtain a better output.

7.     Explain digital multiplexing in detail.

The term digital represents the discrete bits of information. Hence, the available data is in the form of frames or packets, which are discrete.

Time Division Multiplexing (TDM)

In TDM, the time frame is divided into slots. This technique is used to transmit a signal over a single communication channel, by allotting one slot for each message.

Of all the types of TDM, the main ones are Synchronous and Asynchronous TDM.

Synchronous TDM

In Synchronous TDM, the input is connected to a frame. If there are ‘n’ number of connections, then the frame is divided into ‘n’ time slots. One slot is allocated for each input line.

In this technique, the sampling rate is common for all signals and hence the same clock input is given. The MUX allocates the same slot to each device at all times.

Asynchronous TDM

In Asynchronous TDM, the sampling rate is different for each of the signals and a common clock is not required. If the allotted device, for a time slot transmits nothing and sits idle, then that slot is allotted to another device, unlike synchronous.

8.     What are the advantages of DM Over DPCM.

• 1-bit quantizer
• Very easy design of the modulator and the demodulator

However, there exists some noise in DM.

• Slope Over load distortion (when Δ is small)
• Granular noise (when Δ is large)

9.     Write the features and describe delta modulator.

The Delta Modulator comprises of a 1-bit quantizer and a delay circuit along with two summer circuits. Following is the block diagram of a delta modulator.

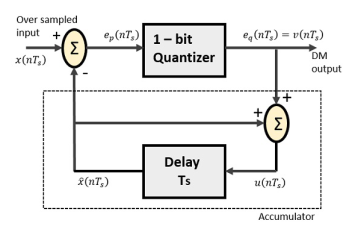
                                                            Fig. : Delta modulation

The predictor circuit in DPCM is replaced by a simple delay circuit in DM.

From the above diagram, we have the notations as −

• x(nTs)= over sampled input
• Ep(nTs) = summer output and quantizer input
• Eq(nTs) = quantizer output = v(nTs)
• xˆ(nTs) = output of delay circuit
• u(nTs) = input of delay circuit

Using these notations, now we shall try to figure out the process of delta modulation.

Ep(nTs)=x(nTs)−xˆ(nTs)           ---------equation 1

=x(nTs)−u([n−1]Ts

=x(nTs)−[xˆ[[n−1]Ts]+v[[n−1]Ts]]  -------equation 2

Further,

v(nTs)=eq(nTs)=S.sig.[ep(nTs)]   ---------equation 3

u(nTs)=xˆ(nTs)+eq(nTs)

Where,

• xˆ(nTs) = the previous value of the delay circuit
• Eq(nTs) = quantizer output = v(nTs)

Hence,

u(nTs)=u([n−1]Ts)+v(nTs)       ---------equation 4

Which means,

The present input of the delay unit

= The previous output of the delay unit + the present quantizer output the present quantizer output

Assuming zero condition of Accumulation,

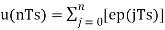
Accumulated version of DM output = 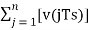         --------equation 5

Now, note that

xˆ(nTs)=u([n−1]Ts)

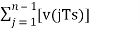=---------equation 6

Delay unit output is an Accumulator output lagging by one sample.

From equations 5 & 6, we get a possible structure for the demodulator.

A Stair-case approximated waveform will be the output of the delta modulator with the step-size as delta (Δ). The output quality of the waveform is moderate.