Unit 1
Signal system
- Define energy and power signals?
A signal is said to be an energy signal when it has finite energy
Energy E = 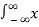 2(t) dt
2(t) dt
Power:
A signal is said to be a power signal when it has finite power.
Power P = lim T-> ∞ 1/2T 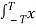 2 (t) dt
2 (t) dt
Energy of CT signal Ex = 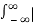 x(t)| 2 dt
x(t)| 2 dt
Energy of discrete time signal Ex = 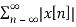 2
2
Power of CT signal Px = lim T-> ∞ 1/2T 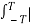 x(t) | 2 dt
x(t) | 2 dt
Power of DT signal Px = lim N-> ∞ 1/2N+1 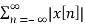 2
2
2.Find the energy of the signal for the following diagram

x(t) = { 3(1-t/4) if 0 
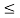 4
4
3(1+t/4) if -4 t
t 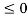
0 otherwise
Therefore
Ex = 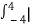 x(t) | 2
x(t) | 2
(Ex = 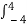 x 2 (t) dt
x 2 (t) dt
= 9 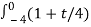 2 dt +
2 dt + 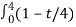 2 dt
2 dt
= 9. (1+t/4) 3 / ¾ | 0 -4 + 9. (1-t/4) 3 /- ¾ | 4 0
= 9 x4/3 + 9x4/3 = 24
Hence Energy Signal
3.What is the difference between continuous and discrete signals?
Continuous systems input and output continuous signals, such as analog electronics where the signal varies continuously with respect to time.
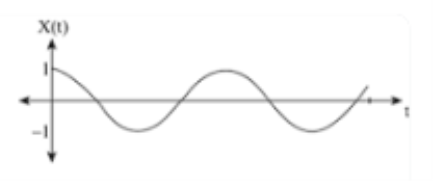
Continuous-time signal
Discrete systems input and output discrete signals, such as computer programs that manipulate the values stored in arrays.
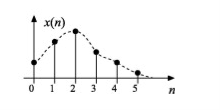
Discrete-time signal
4. Explain linearity property?
Linearity. Basically, the principle of linearity is equivalent to the principle of superposition, i.e. a system can be said to be linear if, for any two input signals, their linear combination yields as output the same linear combination of the corresponding output signals.
For example
A capacitor, an inductor, a resistor, or any combination of these are all linear systems if we consider the voltage applied across them as an input signal and the current through them as an output signal. This is because these simple passive circuit components follow the principle of superposition within their ranges of operation.
Assume y[n] and y(t) are respectively outputs to input signals x[n] and x(t)
System with description y(t) = t. x(t) is linear.
Consider two input signals x1(t) and x2(t) with the corresponding outputs y1(t) and y2(t) where a and b are arbitrary constants. The corresponding output of ax1(t) + b x2(t) is t(ax1(t) + bx2(t))
= t ax1(t) + t b x2(t) which is the same linear combination of y1(t) and y2(t).
Suppose y(t) = |x(t)| 2
Because the system is neither additive nor homogeneous.
5. Explain the property of additivity?
Consider a system where input x1[n] produces an output y1[n]. Similarly x2[n] produces y2[n].
The system is additive when
x1[n] + x2[n] = y1[n] + y2[n]
In other words, signals added at the input will produce signals added at the output.
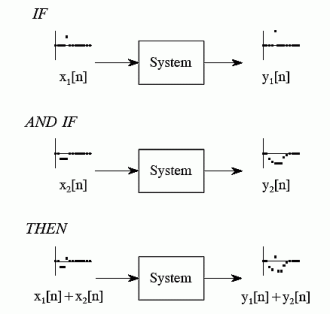
Figure. Addivity
6. Explain the property of Homogeneity?
Homogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude.
That is a change in x[n] will result in a change in y [n]
Also a change in k x[n] will result in a change in k y[n]
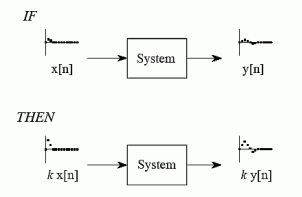
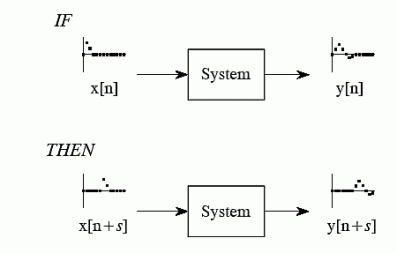
7. What do you mean by shift variance?
Shift invariance means that a shift in the input signal will result in an identical shift in the output signal
If x[n] -> y[n]
Then x[n+s] -> y[n +s] for any constant s
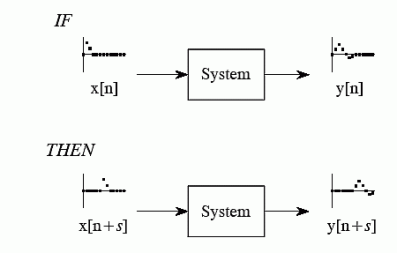
Say, for a system, the input signal x(t) gives rise to an output signal y(t). If the input signal x(t - t0) gives rise to output y(t - t0), for every t0, and every possible input signal, we say the system is shift invariant. i.e. for every permissible x(t) and every t0
x(t) -> y(t) -> x(t-to) -> y(t-to)
In other words, for a shift invariant system, shifting the input signal shifts the output signal by the same offset.
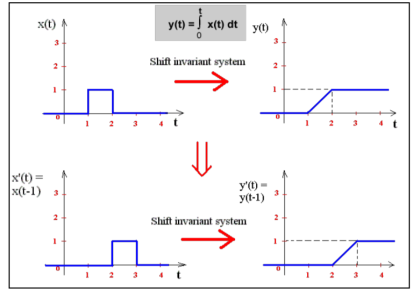
Figure. Shift invariant system
8. Explain causality?
Causal signals are signals that are zero for all negative time. If any value of the output signal depends on a future value of the input signal then the signal is non-causal.
Definition:
Let x1(t) and x2(t) be two input signals to a system and y 1(t) and y2(t) be their respective outputs. The system is said to be causal if and only if:
x1(t) = x2(t) for t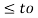
y1(t) = y2( t) for t 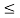 to for every to and for every x1(t) and x2(t)
to for every to and for every x1(t) and x2(t)
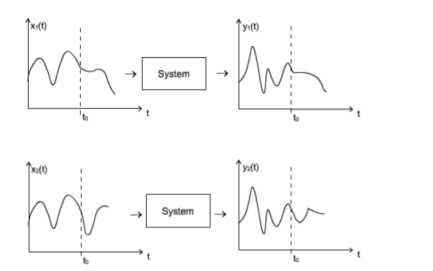
Figure. Casual system
9. Check whether the following systems are casual or not.
y(n) = x(n) + 1/x(n-1)
For n=0
y(0) = x(0) + 1/x(0 -1)
For n=1
y(1) = x(1) + 1/ x(0)
For n=2
y(2) = y(2) + 1/x(1)
For n=-1
y(-1) = x(-1) + 1/x(-2)
For all values of n the output depends on the present and past values of input. Hence the system is casual.
10. Explain BIBO stability?
Bounded input bounded output stability.
The system is BIBO stable if
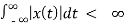
A system is BIBO stable if for any bounded input signal the output signal is bounded.
Given a bounded input i.e Mx 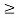 0 |x(t)|
0 |x(t)| 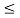 Mx
Mx 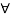 t
t
My 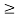 0 |y(t)|
0 |y(t)| 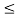 My
My 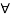 t
t
It is not necessary that for input and output signal to have the same independent variable. It is valid for continuous time, discrete time and hybrid systems.
Suppose
y(t) = {x(t)} 2
If x(t) is bounded then Mx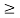 0
0 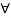 t |x(t)|
t |x(t)| 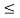 Mx
Mx
|y(t)| 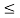 Mx 2
Mx 2
Which further implies that the output is bounded 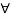 t
t
The system is BIBO stable
Suppose y(t) = t x(t)
Take x(t) = u(t)
Then the input is bounded by 1 and the output is bounded hence BIBO unstable.
11. Explain realizability?
In linear systems theory, the term realizability refers to the ability to characterize a known output in terms of a linear system with some input.
The regressive linear system
x ∆ = A(t)x(t) + B(t)u(t), x(t0) = 0, y(t) = C(t)x(t), of dimension n is a realization of the weighting pattern
G(t, σ(s)) if G(t, σ(s)) = C(t)ΦA(t, σ(s))B(s), for all t, s.
If a realization of this system exists, then the weighting pattern is realizable. The system is a minimal realization if no realization of G(t, σ(s)) with dimension less than n exists.
Unit 1
Signal system
- Define energy and power signals?
A signal is said to be an energy signal when it has finite energy
Energy E = 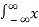 2(t) dt
2(t) dt
Power:
A signal is said to be a power signal when it has finite power.
Power P = lim T-> ∞ 1/2T 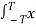 2 (t) dt
2 (t) dt
Energy of CT signal Ex = 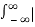 x(t)| 2 dt
x(t)| 2 dt
Energy of discrete time signal Ex = 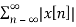 2
2
Power of CT signal Px = lim T-> ∞ 1/2T 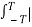 x(t) | 2 dt
x(t) | 2 dt
Power of DT signal Px = lim N-> ∞ 1/2N+1 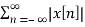 2
2
2.Find the energy of the signal for the following diagram
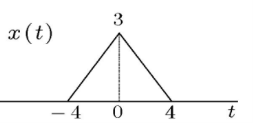
x(t) = { 3(1-t/4) if 0 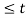
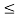 4
4
3(1+t/4) if -4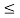 t
t 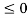
0 otherwise
Therefore
Ex = 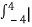 x(t) | 2
x(t) | 2
(Ex = 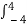 x 2 (t) dt
x 2 (t) dt
= 9 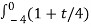 2 dt +
2 dt + 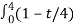 2 dt
2 dt
= 9. (1+t/4) 3 / ¾ | 0 -4 + 9. (1-t/4) 3 /- ¾ | 4 0
= 9 x4/3 + 9x4/3 = 24
Hence Energy Signal
3.What is the difference between continuous and discrete signals?
Continuous systems input and output continuous signals, such as analog electronics where the signal varies continuously with respect to time.
Continuous-time signal
Discrete systems input and output discrete signals, such as computer programs that manipulate the values stored in arrays.
Discrete-time signal
4. Explain linearity property?
Linearity. Basically, the principle of linearity is equivalent to the principle of superposition, i.e. a system can be said to be linear if, for any two input signals, their linear combination yields as output the same linear combination of the corresponding output signals.
For example
A capacitor, an inductor, a resistor, or any combination of these are all linear systems if we consider the voltage applied across them as an input signal and the current through them as an output signal. This is because these simple passive circuit components follow the principle of superposition within their ranges of operation.
Assume y[n] and y(t) are respectively outputs to input signals x[n] and x(t)
System with description y(t) = t. x(t) is linear.
Consider two input signals x1(t) and x2(t) with the corresponding outputs y1(t) and y2(t) where a and b are arbitrary constants. The corresponding output of ax1(t) + b x2(t) is t(ax1(t) + bx2(t))
= t ax1(t) + t b x2(t) which is the same linear combination of y1(t) and y2(t).
Suppose y(t) = |x(t)| 2
Because the system is neither additive nor homogeneous.
5. Explain the property of additivity?
Consider a system where input x1[n] produces an output y1[n]. Similarly x2[n] produces y2[n].
The system is additive when
x1[n] + x2[n] = y1[n] + y2[n]
In other words, signals added at the input will produce signals added at the output.
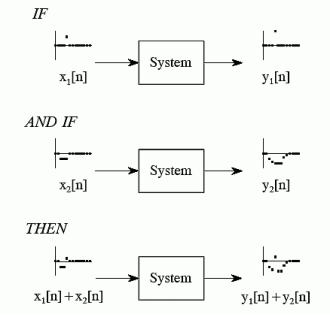
Figure. Addivity
6. Explain the property of Homogeneity?
Homogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude.
That is a change in x[n] will result in a change in y [n]
Also a change in k x[n] will result in a change in k y[n]
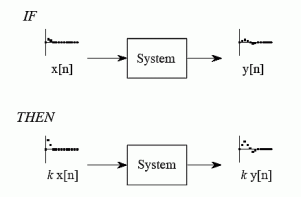
7. What do you mean by shift variance?
Shift invariance means that a shift in the input signal will result in an identical shift in the output signal
If x[n] -> y[n]
Then x[n+s] -> y[n +s] for any constant s
Say, for a system, the input signal x(t) gives rise to an output signal y(t). If the input signal x(t - t0) gives rise to output y(t - t0), for every t0, and every possible input signal, we say the system is shift invariant. i.e. for every permissible x(t) and every t0
x(t) -> y(t) -> x(t-to) -> y(t-to)
In other words, for a shift invariant system, shifting the input signal shifts the output signal by the same offset.
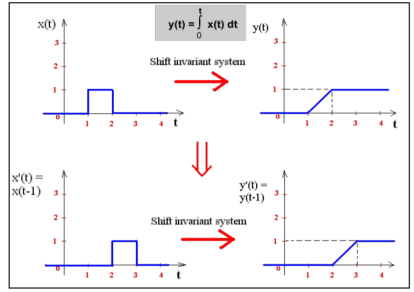
Figure. Shift invariant system
8. Explain causality?
Causal signals are signals that are zero for all negative time. If any value of the output signal depends on a future value of the input signal then the signal is non-causal.
Definition:
Let x1(t) and x2(t) be two input signals to a system and y 1(t) and y2(t) be their respective outputs. The system is said to be causal if and only if:
x1(t) = x2(t) for t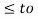
y1(t) = y2( t) for t 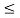 to for every to and for every x1(t) and x2(t)
to for every to and for every x1(t) and x2(t)
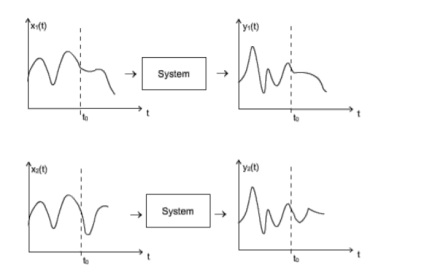
Figure. Casual system
9. Check whether the following systems are casual or not.
y(n) = x(n) + 1/x(n-1)
For n=0
y(0) = x(0) + 1/x(0 -1)
For n=1
y(1) = x(1) + 1/ x(0)
For n=2
y(2) = y(2) + 1/x(1)
For n=-1
y(-1) = x(-1) + 1/x(-2)
For all values of n the output depends on the present and past values of input. Hence the system is casual.
10. Explain BIBO stability?
Bounded input bounded output stability.
The system is BIBO stable if
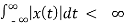
A system is BIBO stable if for any bounded input signal the output signal is bounded.
Given a bounded input i.e Mx 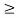 0 |x(t)|
0 |x(t)| 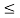 Mx
Mx 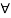 t
t
My 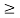 0 |y(t)|
0 |y(t)| 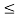 My
My  t
t
It is not necessary that for input and output signal to have the same independent variable. It is valid for continuous time, discrete time and hybrid systems.
Suppose
y(t) = {x(t)} 2
If x(t) is bounded then Mx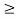 0
0 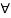 t |x(t)|
t |x(t)| 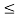 Mx
Mx
|y(t)| 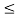 Mx 2
Mx 2
Which further implies that the output is bounded  t
t
The system is BIBO stable
Suppose y(t) = t x(t)
Take x(t) = u(t)
Then the input is bounded by 1 and the output is bounded hence BIBO unstable.
11. Explain realizability?
In linear systems theory, the term realizability refers to the ability to characterize a known output in terms of a linear system with some input.
The regressive linear system
x ∆ = A(t)x(t) + B(t)u(t), x(t0) = 0, y(t) = C(t)x(t), of dimension n is a realization of the weighting pattern
G(t, σ(s)) if G(t, σ(s)) = C(t)ΦA(t, σ(s))B(s), for all t, s.
If a realization of this system exists, then the weighting pattern is realizable. The system is a minimal realization if no realization of G(t, σ(s)) with dimension less than n exists.