Unit 3
Signal system
- Explain Fourier series representation? Derive its expression
A signal is said to be periodic if it satisfies the condition x (t) = x (t + T) or x (n) = x (n + N).
Where T = fundamental time period,
ω0= fundamental frequency = 2π/T
There are two basic periodic signals:
x(t) = cos wot (sinusoidal)
x(t) = e jwot (complex exponential)
These two signals are periodic with period T=2π/ω0
A set of harmonically related complex exponentials can be represented as ɸk(t)
ɸk(t) = { ejkwot} = { e jk(2π/T)t} where k=0,±1,±2,±3,………………(1)
All these signals are periodic with period T.
According to orthogonal signal space approximation of a function f(x) with n mutually orthogonal functions is given by
x(t) = 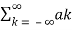 e jkwot ……………………………………………….(2)
e jkwot ……………………………………………….(2)
=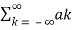 k ejkwot
k ejkwot
Where ak= Fourier coefficient = coefficient of approximation.
This signal x(t) is also periodic with period T.
Equation 2 represents Fourier series representation of periodic signal x(t).
The term k = 0 is constant.
The term k=±1 having fundamental frequency ω0, is called as 1st harmonics.
The term k=±2 having fundamental frequency 2ω0, is called as 2nd harmonics, and so on...
The term k=±n having fundamental frequency nω0, is called as nth harmonics.
Deriving Fourier Coefficient
We know that x(t) = 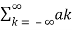 e jkwot ------------------------(1)
e jkwot ------------------------(1)
Multiply e-jnwot on both sides we get
x(t) e -jnwot = 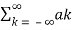 e jkwot . e-jnwot
e jkwot . e-jnwot
Consider integral on both sides we get
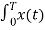 e jkwot dt =
e jkwot dt = 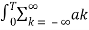 e jkwot. e-jnwot
e jkwot. e-jnwot
= 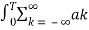 e j(k-n)wotdt
e j(k-n)wotdt
= 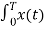 e jkwot dt =
e jkwot dt = 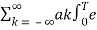 j(k-n)wot dt --------------------------(2)
j(k-n)wot dt --------------------------(2)
By Eulers formula
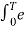 j(k-n)wot dt =
j(k-n)wot dt = 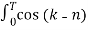 wo dt + j
wo dt + j  wo dt
wo dt
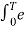 j(k-n)wot dt = { T k=n
j(k-n)wot dt = { T k=n
0 k 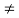 n
n
Hence in equation (2) the integral is zero for all values of k except at k=n. Put k=n is equation 2
= 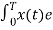 j(k-n)wot dt = anT
j(k-n)wot dt = anT
=an = 1/T 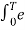 -jnwot
-jnwot
Replace n by k we get
= ak = 1/T 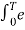 -jkwot dt
-jkwot dt
x(t) =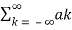 e j(k-n) wot
e j(k-n) wot
Where ak = 1/T 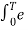 -jkwot dt
-jkwot dt
2. Explain Fourier transform?
Aperiodic signals in continuous time are represented by the Fourier transform
An aperiodic signal can be viewed as a periodic signal with an infinite period
As the period becomes infinite, the frequency components form a continuum and the Fourier series becomes an integral
The (CT) Fourier transform (or spectrum) of x(t) is
X(jw) = 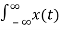 e -jwt dt ---------------------------------------(1)
e -jwt dt ---------------------------------------(1)
x(t) can be reconstructed from its spectrum using the inverse Fourier transform
x(t) = 1/ 2 π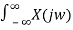 e jwtdw ------------------------------------------(2)
e jwtdw ------------------------------------------(2)
The above two equations are referred as Fourier transform pair with the first one being the analysis equation and the second being the synthesis equation.
Notation
X(jw) = F{x(t)}
x(t) = F -1 {X(jw)}
x(t) and X(jw) form a Fourier transform pair denoted by
 x(t) F X(jw)
x(t) F X(jw)
3. The function is given by
Rect(t) or π(t) = 1 |t| 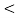 ½
½
0 |t| > ½
½ |t| =1/2
Find the Fourier transform ?
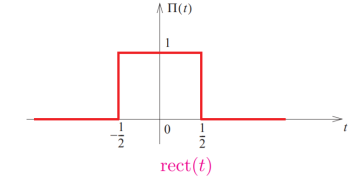
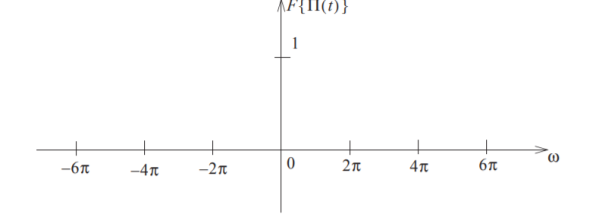
Figure1.Fourier transform of rect
4. Explain its magnitude and phase response ?
H(e jw) = H R ( e jw) + j H I ( e jw) = | H ( e jw) | e j  1 (w)
1 (w)
 1 (w) = angle H(e jw)
1 (w) = angle H(e jw)
Example:
h[n] = - δ[n]
| H (ejw)| = 1 angle H(e jw) = π
In the magnitude or phase representation a real valued frequency response does not mean that the system is zero-phase.
Using this representation,
|Y (ejw) | = | H ( ejw)| | X (ejw)|
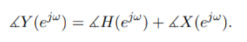
Thus, |H(ejω)| and angle H(ejω) are commonly referred to as the gain and the phase shift of the system, respectively.
In magnitude and phase plots, as ω goes through a zero on the unit circle, the magnitude will go to zero and the phase will flip by π, as shown in the figure below.

Figure. Fourier transform magnitude and frequency response
5. Explain Fourier transform duality ?
The Duality property is very useful because it can enable to solve Fourier Transforms that would be difficult to compute directly (such as taking the Fourier Transform of a sinc function). The Duality Property tells us that if x(t) has a Fourier Transform X(ω), then if we form a new function of time that has the functional form of the transform, X(t), it will have a Fourier Transform x(ω) that has the functional form of the original time function (but is a function of frequency). Mathematically, we can write:
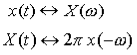

Notice that the second term in the last line is simply the Fourier Transform integral of the function X(t), i.e.

Therefore we get the Duality Property:
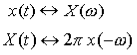
6. Explain DTFT ?
The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.
The DTFT sequence x[n] is given by
X(w) = 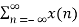 e-jwn ---------------(1)
e-jwn ---------------(1)
Here X(w) is a complex function of real frequency variable w and can be written as
X(w) = Xre (w) + j X img(w)
Where Xre (w) , j X img(w) are real and Imaginary parts of X(w)
Xre (w) = |X(w) cos 
Ximg(w) = |X(w)| sin 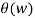
|X(w)| 2 = |Xre(w) | 2 + |Xim(w)| 2
And | X(w)| can be represented as
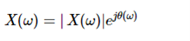 .
.
Inverse Discrete Fourier Transform is given by
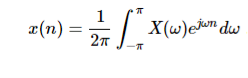
7.Find the four point DFT of the sequence
x(n) = {0,1,2,3}
Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1 for n=0
W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j
W42 = e-j π = cos π – j sin π = -1
W43 = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j
For k=0
X(k) = 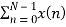 e-j2 π nk/N
e-j2 π nk/N
X(0) =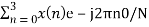
X(0) = x(0)+ x(1)+x(2) + x(3) = 0 +1+2+3 = 6
X(1) = 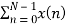 e-j2 π nk/N
e-j2 π nk/N
X(1) = 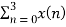 e-j2 π n/4
e-j2 π n/4
= x(0) e0 + x(1) e –j2 π /4+ + x(2) e-j4 π/4+ x(3) e- j 6 π/4
= 0 + 1 –j + 2( -1) + 3(j)
= -2+ 2j
X(2) = 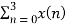 e-j2 π n2/4
e-j2 π n2/4
X(2) = 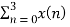 e-j π n
e-j π n
X(2) = x(0) 1+ x(1) e-j π + x(2) e-j2 π + x(3) e-j3 π
X(2) = -2
X(3) =  e-j2 π n3/4
e-j2 π n3/4
X(3) = x(0) e0 + x(1) e-j3 π/2 + x(2) e-j3 π + x(3) e-j9 π/2
X(3) = -2-2j.
DFT = { 6, -2+2j,-2,_2-2j}
8.What is Parseval’s theorem?
Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series co-efficient of these two signals are cn and dn then
1/T  x2(t) = 1/T
x2(t) = 1/T 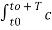 n e j n Ωot [
n e j n Ωot [  m e jmΩot ] dt---------------------(1)
m e jmΩot ] dt---------------------(1)
= 1/T 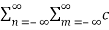 n d *m
n d *m 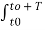 e j(n-m)Ωot dt ------------------------------(2)
e j(n-m)Ωot dt ------------------------------(2)
= 0 n≠ m
= 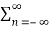 n d *n n=m --------------------------------(3)
n d *n n=m --------------------------------(3)
If x1(t) = x2(t) = x(t) then eq(3) becomes
1/T 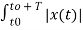 2 =
2 = 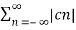 2 --------------------------------(4)
2 --------------------------------(4)
The above equation can be written as
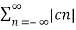 2 = c0 2 +
2 = c0 2 + 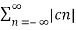 2
2
n≠0
= c0 2 + 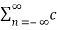 n c *n
n c *n
n≠0
a0 2 + 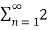 [Re(c 2 n ) + Im (cn ) 2]
[Re(c 2 n ) + Im (cn ) 2]
= a0 2 + 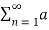 2 n /2 + b 2 n /2 ---------------------------(5)
2 n /2 + b 2 n /2 ---------------------------(5)
9. Explain the condition for orthogonality ?
Signal space (or vector) representation of signals (waveforms) is a very effective and useful tool in the analysis of digitally modulated signals. In fact, any set of signals is equivalent to a set of vectors.
Two vectors u and v are orthogonal if hu, vi = 0. More generally, a set of m vectors v (k) , 1 ≤ k ≤ m, are orthogonal if v (i) , v (j) = 0 for all 1 ≤ i, j ≤ m, and i 6= j.
10.Find the Laplace transform of e–t .
F(s) = 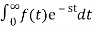
F(s) =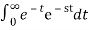
F(s) = 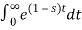
F(s) = 1 / 1-s [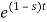 ]0
]0
F(s = 1/ s-1.
11. Explain the eigen functions of LSI system?
A continuous-time Fourier transform (F.T.) is a tool to represent signals as linear combinations of complex exponentials. The exponentials are of the form est with s=j and ejw is an eigen function of the LSI system.
The Fourier Transform only exists for signals which can absolutely integrated and have a finite energy. This observation leads to generalization of continuous-time Fourier transform by considering a broader class of signals using the powerful tool of "Laplace transform".
It will be trivial to note that the L.T can be used to get the discrete-time representation using relevant substitutions. This leads to a link with the Z-Transform and is very handy for a digital filter realization/designing.
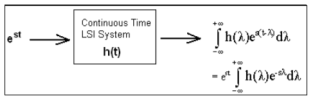
Figure 3. Eigen functions of LSI system
Let H(s) = 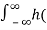 λ) e -sλ dλ
λ) e -sλ dλ
Where H(s) is the Laplace transform of h(t). e st is an eigen LSI system only if H/(s) converges.
12. Explain the basis of eigen functions?
The eigenfunctions are orthogonal. Moreover, the eigenfunctions Φ form a basis for the function space consisting of functions that satisfy the boundary conditions, meaning that any such function can be expressed as a linear combination of the eigenfunctions.
If we have a linear operator, L, with a complete set of orthonormal eigenfunctions, and an inhomogeneous equation
Lu f = we can solve this problem using a basis of eigenfunctions.
We can expand f in terms of the basis
f(x) = 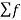 k ɸk(x)
k ɸk(x)
and the solution given as 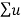 k ɸk(x)
k ɸk(x)
Substituting this into the inhomogeneous equation, we get
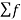 k ɸk(x) = f(x) = Lu = L
k ɸk(x) = f(x) = Lu = L 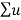 k ɸk(x)=
k ɸk(x)= 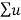 k λ ɸk(x)
k λ ɸk(x)
Equating the coeffecients of ɸk we get the relation
Uk = fk/λk
Since λk ->∞ |fk| are bounded
So we have uk->0
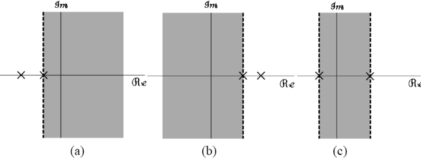
13. Explain the properties of ROC?
Properties of ROC:
Property 1:
The ROC of X(s) consists of strips parallel to the jΩ – axis in the s-plane.
Property 2.
ROC does not contain any poles.
Property 3.
If x(t) is of finite duration and is absolutely integral then ROC is the entire s-plane.
Property 4:
If x(t) is a right sided signal that x(t) = 0 for t<to <∞ then ROC is of the form Re(s) > 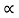 max. Where
max. Where 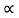 max equals to the maximum real part of any poles of X(s).
max equals to the maximum real part of any poles of X(s).
Property 5:
If x(t) is left-sided that is x(t) =0 for t>t1 >- ∞. Then the ROC is of the form Re(s) < > 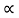 min.
min.
Property 6:
If x(t) is two-sided than the ROC is of the form 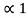 < Re(s) <
< Re(s) < 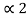
14. Find the Laplace transform of the signal
x(t) = e -3t u(t) + e -2t u(t) and find the ROC
What are the pole-zero location.
X(s) = 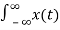 e -st dt
e -st dt
 e -3t u(t) e -st dt +
e -3t u(t) e -st dt + 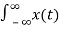 e -2t u(t) e -st dt
e -2t u(t) e -st dt
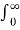 e –(s+3) t dt +
e –(s+3) t dt + 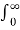 e –(s+2)t dt
e –(s+2)t dt
Converges if Re(s) >-3 and converges if Re(s) > -2
X(s) = -1/s+3 e –(s+3) t | 0 ∞ + -1/s+2 e –(s+2)t | 0 ∞
= 1/s+3 + 1/ s+2 ROC : Re(s) >-2
= 2s + 5 / s2 +5s + 6 ROC 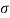 > -2
> -2
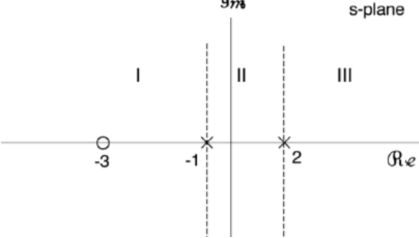
The poles are obtained (s+2)(s+3) at s=-2 and s=-3. and zero is at s=-5/2.





 Re(s) > -2
Re(s) > -2
-2.5 -2
ROC are always vertical half plane stripes bounded by poles.
Right side signals -> ROC in right half plane
Left side signals -> ROC in left half plane
Double sided signals -> ROC in a central stripe or does not exist.
XX(s) = s+3/ (s+1) (s-2) = A/ s+1 + B/s-2
AA = -2/3 B = 5/3
1/s + 1 = e-t
1/ s-2 = e 2t
15.Explain poles and zeros of the system?
All Laplace transforms in the above examples are rational, i.e., they can be written as a ratio of polynomials of variable 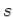 in the general form
in the general form
X(s) = N(s) / D(s) = 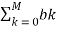 s k /
s k / 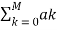 s k =
s k = 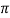 k=1 M (s-szk)/ (s-spk)
k=1 M (s-szk)/ (s-spk)
- N(s) is the numerator polynomial of order M with roots szk(k=0,1,2…….M),
- D(s) is the denominator polynomial of order N with roots with spk =(1,2………N).
In general, we assume the order of the numerator polynomial is always lower than that of the denominator polynomial, M<N. If this is not the case, we can always expand X(s) into multiple terms so that M<N is true for each of terms.
16. Solve the following IVP
y′′−10y′+9y=5t,y(0)=−1y′(0)=2y″−10y′+9y=5t,y(0)=−1y′(0)=2
The first step in using Laplace transforms to solve an IVP is to take the transform of every term in the differential equation.
L{y’’} – 10L {y’} + 9L{y} = L{5t}
s 2 Y(s) – s y(0) – y’(0) – 10 (sY(s) – y(0) ) + 9Y (s) = 5/ s 2
Plug in the initial conditions we get
(s 2 – 10s +9) Y(s) +s -12= 5/ s2
Solve for Y(s)
Y(s) = 5/ s2 (s-9) (s-1) + 12-s / (s-9) (s-1)
Combining the two terms we get
Y(s) = 5+12 s2 – s3 / s2 (s-9) (s-1)
The partial fraction decomposition for this transform is,
Y(s) = A/s + B/ s2 + C /s-9 + d/s-1
A = 50/81; B = 5/9 ; C= 31/81; D=-2
Taking inverse transform gives us
y(t) = 50/81 + 5/9 t + 31/81 e 9t – 2 et
Unit 3
Signal system
- Explain Fourier series representation? Derive its expression
A signal is said to be periodic if it satisfies the condition x (t) = x (t + T) or x (n) = x (n + N).
Where T = fundamental time period,
ω0= fundamental frequency = 2π/T
There are two basic periodic signals:
x(t) = cos wot (sinusoidal)
x(t) = e jwot (complex exponential)
These two signals are periodic with period T=2π/ω0
A set of harmonically related complex exponentials can be represented as ɸk(t)
ɸk(t) = { ejkwot} = { e jk(2π/T)t} where k=0,±1,±2,±3,………………(1)
All these signals are periodic with period T.
According to orthogonal signal space approximation of a function f(x) with n mutually orthogonal functions is given by
x(t) =  e jkwot ……………………………………………….(2)
e jkwot ……………………………………………….(2)
=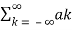 k ejkwot
k ejkwot
Where ak= Fourier coefficient = coefficient of approximation.
This signal x(t) is also periodic with period T.
Equation 2 represents Fourier series representation of periodic signal x(t).
The term k = 0 is constant.
The term k=±1 having fundamental frequency ω0, is called as 1st harmonics.
The term k=±2 having fundamental frequency 2ω0, is called as 2nd harmonics, and so on...
The term k=±n having fundamental frequency nω0, is called as nth harmonics.
Deriving Fourier Coefficient
We know that x(t) = 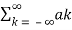 e jkwot ------------------------(1)
e jkwot ------------------------(1)
Multiply e-jnwot on both sides we get
x(t) e -jnwot = 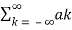 e jkwot . e-jnwot
e jkwot . e-jnwot
Consider integral on both sides we get
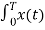 e jkwot dt =
e jkwot dt = 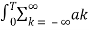 e jkwot. e-jnwot
e jkwot. e-jnwot
= 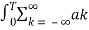 e j(k-n)wotdt
e j(k-n)wotdt
= 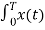 e jkwot dt =
e jkwot dt =  j(k-n)wot dt --------------------------(2)
j(k-n)wot dt --------------------------(2)
By Eulers formula
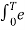 j(k-n)wot dt =
j(k-n)wot dt = 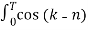 wo dt + j
wo dt + j 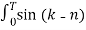 wo dt
wo dt
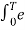 j(k-n)wot dt = { T k=n
j(k-n)wot dt = { T k=n
0 k 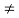 n
n
Hence in equation (2) the integral is zero for all values of k except at k=n. Put k=n is equation 2
= 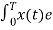 j(k-n)wot dt = anT
j(k-n)wot dt = anT
=an = 1/T 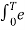 -jnwot
-jnwot
Replace n by k we get
= ak = 1/T 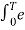 -jkwot dt
-jkwot dt
x(t) =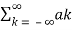 e j(k-n) wot
e j(k-n) wot
Where ak = 1/T 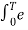 -jkwot dt
-jkwot dt
2. Explain Fourier transform?
Aperiodic signals in continuous time are represented by the Fourier transform
An aperiodic signal can be viewed as a periodic signal with an infinite period
As the period becomes infinite, the frequency components form a continuum and the Fourier series becomes an integral
The (CT) Fourier transform (or spectrum) of x(t) is
X(jw) = 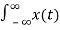 e -jwt dt ---------------------------------------(1)
e -jwt dt ---------------------------------------(1)
x(t) can be reconstructed from its spectrum using the inverse Fourier transform
x(t) = 1/ 2 π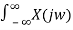 e jwtdw ------------------------------------------(2)
e jwtdw ------------------------------------------(2)
The above two equations are referred as Fourier transform pair with the first one being the analysis equation and the second being the synthesis equation.
Notation
X(jw) = F{x(t)}
x(t) = F -1 {X(jw)}
x(t) and X(jw) form a Fourier transform pair denoted by
 x(t) F X(jw)
x(t) F X(jw)
3. The function is given by
Rect(t) or π(t) = 1 |t| 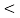 ½
½
0 |t| > ½
½ |t| =1/2
Find the Fourier transform ?
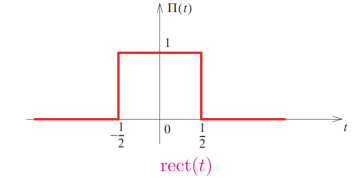
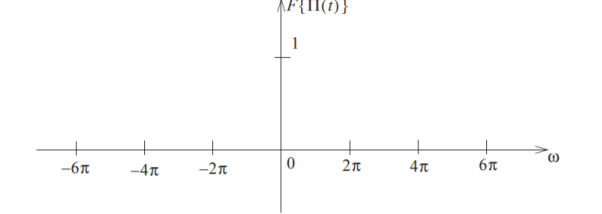
Figure1.Fourier transform of rect
4. Explain its magnitude and phase response ?
H(e jw) = H R ( e jw) + j H I ( e jw) = | H ( e jw) | e j 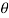 1 (w)
1 (w)
 1 (w) = angle H(e jw)
1 (w) = angle H(e jw)
Example:
h[n] = - δ[n]
| H (ejw)| = 1 angle H(e jw) = π
In the magnitude or phase representation a real valued frequency response does not mean that the system is zero-phase.
Using this representation,
|Y (ejw) | = | H ( ejw)| | X (ejw)|
Thus, |H(ejω)| and angle H(ejω) are commonly referred to as the gain and the phase shift of the system, respectively.
In magnitude and phase plots, as ω goes through a zero on the unit circle, the magnitude will go to zero and the phase will flip by π, as shown in the figure below.
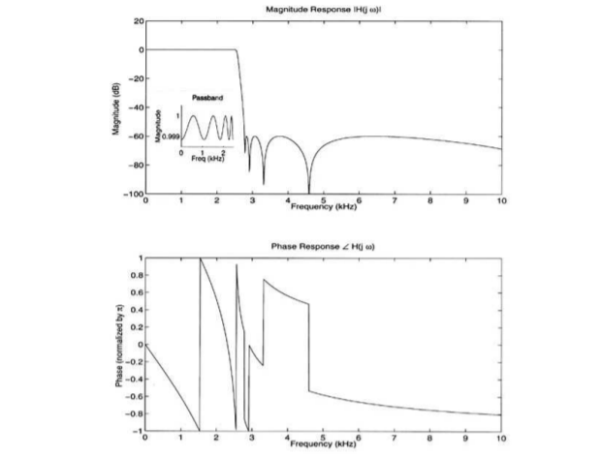
Figure. Fourier transform magnitude and frequency response
5. Explain Fourier transform duality ?
The Duality property is very useful because it can enable to solve Fourier Transforms that would be difficult to compute directly (such as taking the Fourier Transform of a sinc function). The Duality Property tells us that if x(t) has a Fourier Transform X(ω), then if we form a new function of time that has the functional form of the transform, X(t), it will have a Fourier Transform x(ω) that has the functional form of the original time function (but is a function of frequency). Mathematically, we can write:
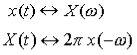

Notice that the second term in the last line is simply the Fourier Transform integral of the function X(t), i.e.

Therefore we get the Duality Property:
6. Explain DTFT ?
The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.
The DTFT sequence x[n] is given by
X(w) =  e-jwn ---------------(1)
e-jwn ---------------(1)
Here X(w) is a complex function of real frequency variable w and can be written as
X(w) = Xre (w) + j X img(w)
Where Xre (w) , j X img(w) are real and Imaginary parts of X(w)
Xre (w) = |X(w) cos 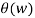
Ximg(w) = |X(w)| sin 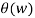
|X(w)| 2 = |Xre(w) | 2 + |Xim(w)| 2
And | X(w)| can be represented as
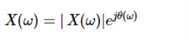 .
.
Inverse Discrete Fourier Transform is given by
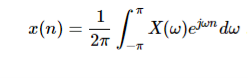
7.Find the four point DFT of the sequence
x(n) = {0,1,2,3}
Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1 for n=0
W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j
W42 = e-j π = cos π – j sin π = -1
W43 = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j
For k=0
X(k) = 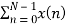 e-j2 π nk/N
e-j2 π nk/N
X(0) =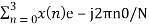
X(0) = x(0)+ x(1)+x(2) + x(3) = 0 +1+2+3 = 6
X(1) = 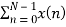 e-j2 π nk/N
e-j2 π nk/N
X(1) = 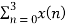 e-j2 π n/4
e-j2 π n/4
= x(0) e0 + x(1) e –j2 π /4+ + x(2) e-j4 π/4+ x(3) e- j 6 π/4
= 0 + 1 –j + 2( -1) + 3(j)
= -2+ 2j
X(2) = 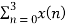 e-j2 π n2/4
e-j2 π n2/4
X(2) = 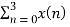 e-j π n
e-j π n
X(2) = x(0) 1+ x(1) e-j π + x(2) e-j2 π + x(3) e-j3 π
X(2) = -2
X(3) = 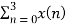 e-j2 π n3/4
e-j2 π n3/4
X(3) = x(0) e0 + x(1) e-j3 π/2 + x(2) e-j3 π + x(3) e-j9 π/2
X(3) = -2-2j.
DFT = { 6, -2+2j,-2,_2-2j}
8.What is Parseval’s theorem?
Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series co-efficient of these two signals are cn and dn then
1/T  x2(t) = 1/T
x2(t) = 1/T 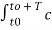 n e j n Ωot [
n e j n Ωot [ 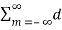 m e jmΩot ] dt---------------------(1)
m e jmΩot ] dt---------------------(1)
= 1/T  n d *m
n d *m 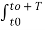 e j(n-m)Ωot dt ------------------------------(2)
e j(n-m)Ωot dt ------------------------------(2)
= 0 n≠ m
= 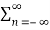 n d *n n=m --------------------------------(3)
n d *n n=m --------------------------------(3)
If x1(t) = x2(t) = x(t) then eq(3) becomes
1/T  2 =
2 = 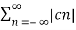 2 --------------------------------(4)
2 --------------------------------(4)
The above equation can be written as
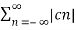 2 = c0 2 +
2 = c0 2 +  2
2
n≠0
= c0 2 + 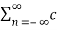 n c *n
n c *n
n≠0
a0 2 +  [Re(c 2 n ) + Im (cn ) 2]
[Re(c 2 n ) + Im (cn ) 2]
= a0 2 + 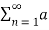 2 n /2 + b 2 n /2 ---------------------------(5)
2 n /2 + b 2 n /2 ---------------------------(5)
9. Explain the condition for orthogonality ?
Signal space (or vector) representation of signals (waveforms) is a very effective and useful tool in the analysis of digitally modulated signals. In fact, any set of signals is equivalent to a set of vectors.
Two vectors u and v are orthogonal if hu, vi = 0. More generally, a set of m vectors v (k) , 1 ≤ k ≤ m, are orthogonal if v (i) , v (j) = 0 for all 1 ≤ i, j ≤ m, and i 6= j.
10.Find the Laplace transform of e–t .
F(s) = 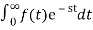
F(s) =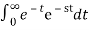
F(s) = 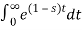
F(s) = 1 / 1-s [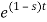 ]0
]0
F(s = 1/ s-1.
11. Explain the eigen functions of LSI system?
A continuous-time Fourier transform (F.T.) is a tool to represent signals as linear combinations of complex exponentials. The exponentials are of the form est with s=j and ejw is an eigen function of the LSI system.
The Fourier Transform only exists for signals which can absolutely integrated and have a finite energy. This observation leads to generalization of continuous-time Fourier transform by considering a broader class of signals using the powerful tool of "Laplace transform".
It will be trivial to note that the L.T can be used to get the discrete-time representation using relevant substitutions. This leads to a link with the Z-Transform and is very handy for a digital filter realization/designing.

Figure 3. Eigen functions of LSI system
Let H(s) = 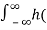 λ) e -sλ dλ
λ) e -sλ dλ
Where H(s) is the Laplace transform of h(t). e st is an eigen LSI system only if H/(s) converges.
12. Explain the basis of eigen functions?
The eigenfunctions are orthogonal. Moreover, the eigenfunctions Φ form a basis for the function space consisting of functions that satisfy the boundary conditions, meaning that any such function can be expressed as a linear combination of the eigenfunctions.
If we have a linear operator, L, with a complete set of orthonormal eigenfunctions, and an inhomogeneous equation
Lu f = we can solve this problem using a basis of eigenfunctions.
We can expand f in terms of the basis
f(x) =  k ɸk(x)
k ɸk(x)
and the solution given as 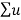 k ɸk(x)
k ɸk(x)
Substituting this into the inhomogeneous equation, we get
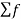 k ɸk(x) = f(x) = Lu = L
k ɸk(x) = f(x) = Lu = L 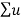 k ɸk(x)=
k ɸk(x)= 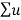 k λ ɸk(x)
k λ ɸk(x)
Equating the coeffecients of ɸk we get the relation
Uk = fk/λk
Since λk ->∞ |fk| are bounded
So we have uk->0
13. Explain the properties of ROC?
Properties of ROC:
Property 1:
The ROC of X(s) consists of strips parallel to the jΩ – axis in the s-plane.
Property 2.
ROC does not contain any poles.
Property 3.
If x(t) is of finite duration and is absolutely integral then ROC is the entire s-plane.
Property 4:
If x(t) is a right sided signal that x(t) = 0 for t<to <∞ then ROC is of the form Re(s) > 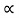 max. Where
max. Where 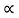 max equals to the maximum real part of any poles of X(s).
max equals to the maximum real part of any poles of X(s).
Property 5:
If x(t) is left-sided that is x(t) =0 for t>t1 >- ∞. Then the ROC is of the form Re(s) < >  min.
min.
Property 6:
If x(t) is two-sided than the ROC is of the form  < Re(s) <
< Re(s) < 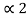
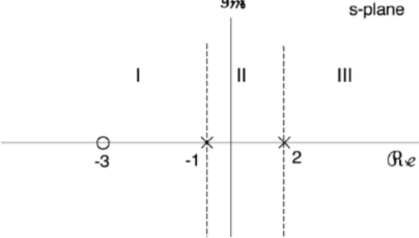
14. Find the Laplace transform of the signal
x(t) = e -3t u(t) + e -2t u(t) and find the ROC
What are the pole-zero location.
X(s) = 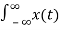 e -st dt
e -st dt
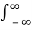 e -3t u(t) e -st dt +
e -3t u(t) e -st dt + 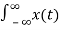 e -2t u(t) e -st dt
e -2t u(t) e -st dt
 e –(s+3) t dt +
e –(s+3) t dt + 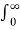 e –(s+2)t dt
e –(s+2)t dt
Converges if Re(s) >-3 and converges if Re(s) > -2
X(s) = -1/s+3 e –(s+3) t | 0 ∞ + -1/s+2 e –(s+2)t | 0 ∞
= 1/s+3 + 1/ s+2 ROC : Re(s) >-2
= 2s + 5 / s2 +5s + 6 ROC 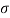 > -2
> -2
The poles are obtained (s+2)(s+3) at s=-2 and s=-3. and zero is at s=-5/2.





 Re(s) > -2
Re(s) > -2
-2.5 -2
ROC are always vertical half plane stripes bounded by poles.
Right side signals -> ROC in right half plane
Left side signals -> ROC in left half plane
Double sided signals -> ROC in a central stripe or does not exist.
XX(s) = s+3/ (s+1) (s-2) = A/ s+1 + B/s-2
AA = -2/3 B = 5/3
1/s + 1 = e-t
1/ s-2 = e 2t
15.Explain poles and zeros of the system?
All Laplace transforms in the above examples are rational, i.e., they can be written as a ratio of polynomials of variable 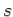 in the general form
in the general form
X(s) = N(s) / D(s) =  s k /
s k / 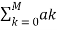 s k =
s k = 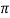 k=1 M (s-szk)/ (s-spk)
k=1 M (s-szk)/ (s-spk)
- N(s) is the numerator polynomial of order M with roots szk(k=0,1,2…….M),
- D(s) is the denominator polynomial of order N with roots with spk =(1,2………N).
In general, we assume the order of the numerator polynomial is always lower than that of the denominator polynomial, M<N. If this is not the case, we can always expand X(s) into multiple terms so that M<N is true for each of terms.
16. Solve the following IVP
y′′−10y′+9y=5t,y(0)=−1y′(0)=2y″−10y′+9y=5t,y(0)=−1y′(0)=2
The first step in using Laplace transforms to solve an IVP is to take the transform of every term in the differential equation.
L{y’’} – 10L {y’} + 9L{y} = L{5t}
s 2 Y(s) – s y(0) – y’(0) – 10 (sY(s) – y(0) ) + 9Y (s) = 5/ s 2
Plug in the initial conditions we get
(s 2 – 10s +9) Y(s) +s -12= 5/ s2
Solve for Y(s)
Y(s) = 5/ s2 (s-9) (s-1) + 12-s / (s-9) (s-1)
Combining the two terms we get
Y(s) = 5+12 s2 – s3 / s2 (s-9) (s-1)
The partial fraction decomposition for this transform is,
Y(s) = A/s + B/ s2 + C /s-9 + d/s-1
A = 50/81; B = 5/9 ; C= 31/81; D=-2
Taking inverse transform gives us
y(t) = 50/81 + 5/9 t + 31/81 e 9t – 2 et