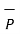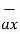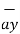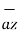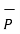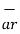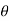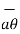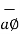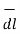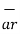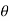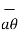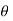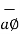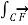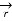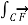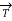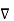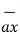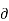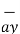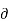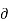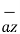Unit - 1
Coordinate Systems and Transformations
Q1) Explain rectangular co-ordinate system?
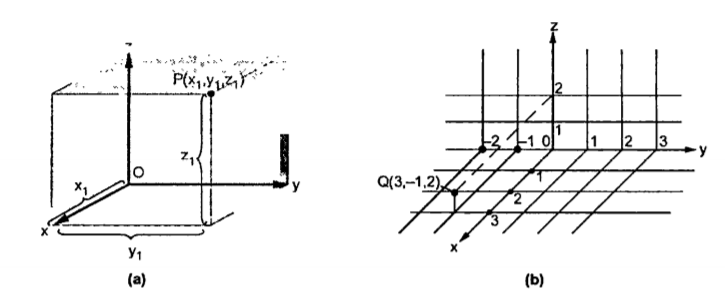
Representing a point in Rectangular Co-ordinate system
A point in rectangular co-ordinate system is located by three co-ordinates namely x,y and z co-ordinates. The point can be reached by moving from origin the distance of x in x-direction , distance of y in y-direction and finally distance of z in z direction.
Consider a point P having co-ordinates x1,y1 and z1 which can be positive or negative.
The point Q(3,-1,2) can be shown as
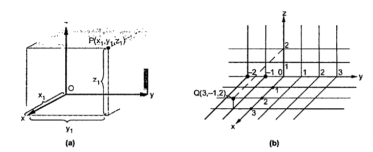
Figure 1. Rectangular co-ordinate system
Base vector :
The base vector are the unit vectors that are oriented along the directions of the co-ordinate axes of the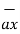 given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore
given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore 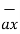 ,
, 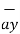 and
and 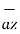 are the base vectors of the cartesian co-ordinate system.
are the base vectors of the cartesian co-ordinate system.
Any point of the x-axis having (x1,0,0) can be represented by a vector joining origin to this point to this point and denoted as x1 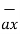 .
.
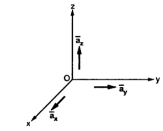
Figure 2. Base vector
Position and Distance vectors :
Consider a point P(x1, y1, z1) in cartesian co-ordinate system as shown in figure. Then the position vector of point P from the origin directed from origin to point P. This is called radius vector as shown in figure.
The three components of position vector oriented along the three co-ordinate axes with magnitudes x1, y1and z1. Thus the position vector of point P can be represented as
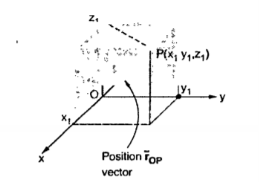
Figure 3. Position vector
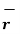 OP = x1
OP = x1 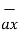 + y1
+ y1 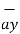 + z1
+ z1 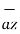
The magnitude of this vector in terms of three mutually perpendicular components is given by
|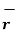 OP |=
OP |= 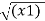 2 + (y1) 2 + (z1) 2
2 + (y1) 2 + (z1) 2
Thus, if point P has co-ordinates (1,2,3) then its position vector is
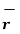 OP =1
OP =1 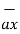 + 2
+ 2 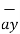 + 3
+ 3 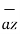
And
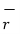 OP =
OP = 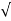 (1) 2 + (2) 2 + (3) 2 =
(1) 2 + (2) 2 + (3) 2 = 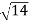 = 3.7416
= 3.7416
Consider two points in a cartesian coordinate system P and Q with the co-ordinates (x1,y1,z1) and (x2,y2,z2) respectively. The individual position vector of the points are
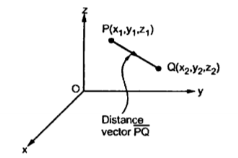
Figure 4. Cartesian coordinate system
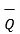 = x2
= x2 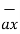 + y2
+ y2 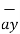 + z2
+ z2 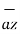
Then the displacement from P to Q is represented by the distance vector 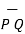 and is given by
and is given by
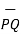 =
= 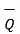 -
- 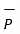 = [x2 -x1]
= [x2 -x1] 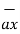 + [ y2 -y1]
+ [ y2 -y1] 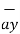 + [z2 -z1]
+ [z2 -z1] 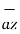
This is called separation vector.
The magnitude of the vector is given by
|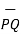 | = √ (x2 -x1) 2 + (y2 -y1) 2 +(z2 – z1) 2
| = √ (x2 -x1) 2 + (y2 -y1) 2 +(z2 – z1) 2
This is called as distance formula.
The unit vector along the direction PQ is given by
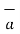 PQ = Unit vector along PQ =
PQ = Unit vector along PQ = 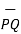 / |PQ|
/ |PQ|
Q2) Given the three points in cartesian co-ordinate system as A(3,-2,1) B (-3,-3,5) , C (2,6,-4)
Find
i) The vector from A to C
ii) The unit vector from B to A
iii) The distance from B to C
iv) The vector from A to the mid-point of the straight line joining B to C.
The position vectors for the given points are:
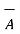 = 3
= 3 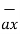 - 2
- 2 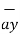 +
+ 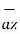 .
.
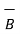 = -3
= -3 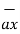 - 3
- 3 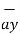 + 5
+ 5 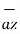 .
.
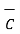 = 2
= 2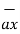 +6
+6 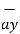 -4
-4 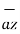 .
.
i) The vector from A to C is
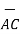 =
= 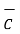 -
- 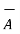 = [ 2-3]
= [ 2-3] 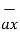 +[6 –(-2)]
+[6 –(-2)] 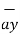 +[-4-1]
+[-4-1] 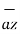 .
.
= - 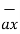 + 8
+ 8 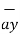 -5
-5 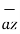 .
.
ii) For unit vector from B to A obtain the distance vector 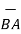 first
first
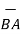 =
= 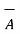 -
- 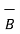
= [ 3 – (-3)]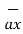 + [ (-2) –(-3) ]
+ [ (-2) –(-3) ] 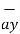 + [ -4-1]
+ [ -4-1] 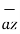
= 6 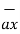 +
+ 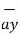 -4
-4 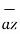 .
.
|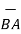 | =
| = 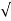 (6) 2 + (1) 2 + (-4)2 = 7.2801.
(6) 2 + (1) 2 + (-4)2 = 7.2801.
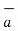 BA =
BA = 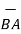 / |
/ |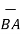 | = 6
| = 6 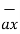 +
+ 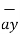 -4
-4 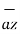 ./ 7.2801
./ 7.2801
iii) For distance between B and C
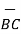 =
= 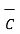 -
- 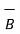 = [ 2 –(-3 ]
= [ 2 –(-3 ] 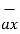 + [6-(-3)]
+ [6-(-3)] 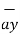 +[-4) –(-5)]
+[-4) –(-5)] 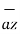 = 5
= 5 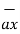 + 9
+ 9 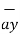 – 9
– 9 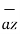
Distance BC = 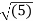 2 + (9) 2 + (-9) 2 = 13.6747
2 + (9) 2 + (-9) 2 = 13.6747
iv) Let B(x1,y1,z1 ) and C(x2,y2,z2) then the co-ordinates of the mid-point BC are (x1+x2/2 , y1+y2/2 , z1+z2/2)
Q3) Explain spherical coordinate system?
The surfaces which are used to define the spherical co-ordinate system on the three cartesian axes are:
Thus the three co-ordinates of a point P in the spherical co-ordinate system are (r,Ѳ,Ø). These surfaces are shown in figure
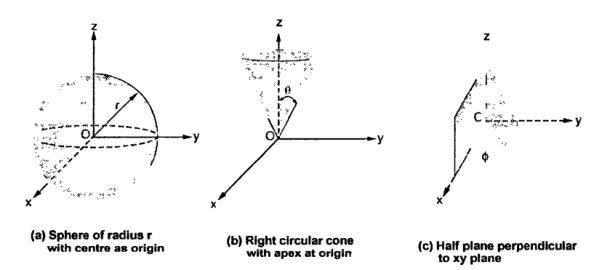
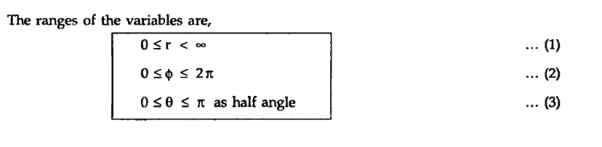
Figure 9. Spherical coordinate system.
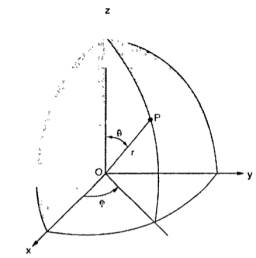
Figure 10. Points in the spherical coordinate system
The point P(r,Ѳ,Ø) can be represented in the spherical co-ordinate system as shown in figure. The angles Ѳ and Ø are measured in radians. The point P can be defined as the intersection of three surfaces in spherical co-ordinate system. These three surfaces are:
r = Constant which is a sphere with cenre as origin
Ɵ = Constant which is right circular cone with apex as origin and axis a z axis
ɸ= Constant is a plane perpendicular to xy plane.
Base Vector:
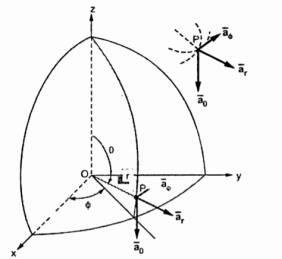
Figure 11. Base vector
There are three unit vectors in r, Ɵ and ɸ directions denoted as 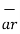 ,
, 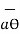 and
and 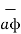 . These unit vectors are mutually perpendicular to each other as shown in figure. The unit vector
. These unit vectors are mutually perpendicular to each other as shown in figure. The unit vector 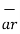 is directed from the centre of the sphere that is the origin to the given point P. It is radially outward normal to the sphere. It lies in the cone Ɵ = constant and plane ɸ= constant.
is directed from the centre of the sphere that is the origin to the given point P. It is radially outward normal to the sphere. It lies in the cone Ɵ = constant and plane ɸ= constant.
The unit vector 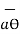 is tangent to the sphere and oriented in the direction of increasing Ɵ. It is normal to the conical surface.
is tangent to the sphere and oriented in the direction of increasing Ɵ. It is normal to the conical surface.
The third unit vector 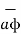 is tangent to the sphere and also tangent to the conical surface. It is oriented in the direction of increasing ɸ. It is same as defined in the cylindrical co-ordinate system.
is tangent to the sphere and also tangent to the conical surface. It is oriented in the direction of increasing ɸ. It is same as defined in the cylindrical co-ordinate system.
Hence, vector P is
Differential elements in Spherical co-ordinate system.
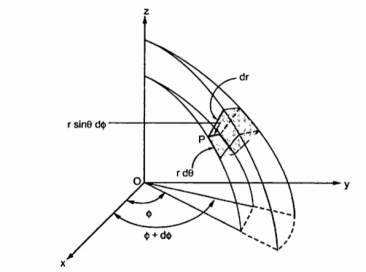
Figure 12. Spherical coordinate system
Consider a point P(r,Ɵ,ɸ) in spherical co-ordinate system. Let each co-ordinate be increased by the differential amount. The differential increments in r,Ɵ,ɸ are dr,dƟ and dɸ.
Now there are two spheres of radius r and r+dr . There are two cones with half angles Ɵ and Ɵ+dƟ. There are two planes at the angles ɸ+dɸ measured from xz plane. All these surfaces enclose a small volume as shown in figure.
dr= Differential length in r direction
r d Ɵ = Differential length in Ɵ direction
r sin Ɵ dɸ = Differential length in ɸ direction.
Hence the differential vector length in spherical coordinate system is
The magnitude of the differential length vector is
|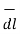 | = √ (dr) 2 + (r d
| = √ (dr) 2 + (r d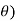 2 + (r sin
2 + (r sin 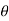 dɸ) 2
dɸ) 2
Hence differential volume is given by
dv = r 2 sin 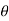 dr d
dr d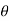 d
d 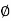
Q4) Write a short note on vector calculus?
Consider a scalar valued function of scalar for example time -dependent density of a material 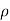 =
= 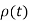
Consider vector valued function of scalar for example time -dependent displacement of a particle u = u(t). In this case the derivative in the usual way
du/dt = lim ∆t->0 u(t+∆t) – u(t) / ∆t
which turns out to be simply the derivative co-efficient
du/dt = du1/dt e1 + du2/dt e2 + du3/dt = dui/dt ei
Partial differentiation:
Partial derivatives can also be defined. For example if u is a function of the coordinates u(x1,x2,x3) then
∂u/ ∂x1 = lim ∆x1->0 u(x1+ ∆x1 ,x2,x3) – u( x1,x2,x3) / ∆x1
Integration
The line integrals of vector fields as a line integral with respect to arc length as follows,
where →T(t) is the unit tangent vector and is given by,
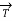 (t) =
(t) = 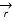 ’(t) ||
’(t) ||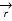 ’(t)||
’(t)||
To compute line integrals with respect to arc length we can see that this second form is equivalent to the first form given above.
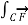 . d
. d 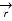 =
= 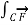 .
. 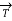 ds
ds
= 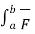 (
( 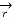 ‘(t) / ||
‘(t) / || 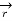 ‘(t) || ||
‘(t) || ||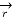 ‘(t) || dt
‘(t) || dt
= 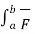 (
( 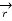 ‘(t) ) .
‘(t) ) . 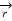 ‘(t) dt
‘(t) dt
Q5) Explain line surface and volume integrals?
The electric field intensity due to point charge Q is given by
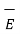 = Q/ 4 π
= Q/ 4 π 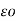 R 2
R 2 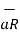
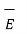 due to line charge:
due to line charge:
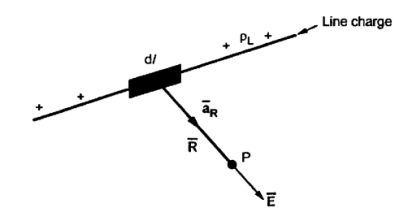
Figure . Line charge
Consider a line charge distribution having charge density 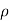 L as shown in figure.
L as shown in figure.
The charge dQ on the differential length dl is
dQ = 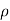 L dl----------------(1)
L dl----------------(1)
Hence the differential electric field d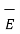 at point P due to dQ is given by
at point P due to dQ is given by
d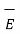 = dQ/ 4
= dQ/ 4 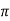
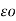 R 2
R 2 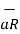 =
= 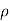 L dl / 4
L dl / 4 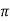
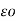 R 2
R 2 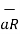 ----------------------(2)
----------------------(2)
Hence the total 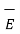 at a point P due to line charge can be obtained by integrating d
at a point P due to line charge can be obtained by integrating d 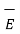 over the length of the charge.
over the length of the charge.
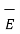 =
= 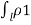 dl/ 4
dl/ 4 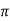
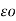 R 2
R 2 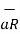
The 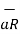 and dl can be obtained depending upon the coordinate system used.
and dl can be obtained depending upon the coordinate system used.
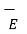 due to surface charge.
due to surface charge.
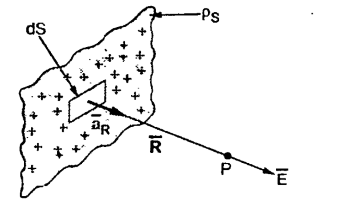
Figure . Surface charge
Consider a surface charge distribution having a charge density 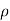 s as shown in the figure. The charge dQ on the differential surface area dS is
s as shown in the figure. The charge dQ on the differential surface area dS is
dQ = 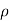 s dS.
s dS.
Hence the differential electric field d 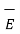 at a point due to dQ is given by,
at a point due to dQ is given by,
d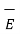 = dQ/ 4
= dQ/ 4 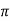
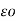 R 2
R 2 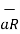 =
= 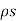 dS/ 4
dS/ 4 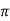
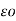 R 2
R 2 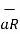
Hence the total 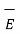 at a point P is to be obtained by integrating d
at a point P is to be obtained by integrating d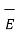 over the surface area on which charge is distributed.
over the surface area on which charge is distributed.
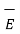 due to Volume charge
due to Volume charge
Consider a volume charge distribution having a charge density 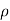 v as shown in the figure.
v as shown in the figure.
The charge dQ on the differential volume dv is
dQ = 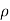 v dv
v dv
Hence the differential electric field d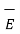 at a point P due to dQ is given by
at a point P due to dQ is given by
d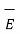 = dQ/ 4
= dQ/ 4 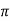
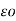 R 2
R 2 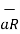 =
= 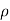 v dv/ 4
v dv/ 4 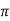
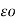 R 2
R 2 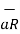
Hence the total 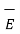 at a point P is to be obtained by integrating d
at a point P is to be obtained by integrating d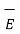 over the volume in which charge is accumulated.
over the volume in which charge is accumulated.
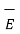 =
= 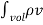 dv / 4
dv / 4 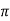
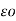 R 2
R 2 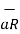
The 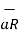 and dv must be obtained according to the co-ordinate system used.
and dv must be obtained according to the co-ordinate system used.
Thus, if there are all possible types of charge distribution then the total 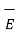 at a point is the vector sum of individual electric field intensities produced by each of the charges at a point under consideration.
at a point is the vector sum of individual electric field intensities produced by each of the charges at a point under consideration.
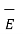 total =
total = 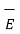 p +
p + 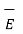 l +
l + 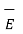 s +
s + 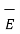 v
v
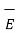 p ,
p , 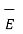 l ,
l , 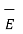 s ,
s , 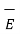 v are the field intensities due to point , line, surface and volume charge distributions respectively.
v are the field intensities due to point , line, surface and volume charge distributions respectively.
Q6) Explain del operator and gradient?
Consider that in space let W be the unique function of x,y,z co-ordinates in the cartesian system. This is scalar function denoted as W(x,y,z) . Consider the vector operator in cartesian system denoted as 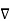 called del. It is defined as
called del. It is defined as
Gradient
Let ɸ(x) be a scalar field. The gradient of ɸ is vector field defined as
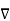 ɸ = ∂ɸ/ ∂x1 e1 + ∂ɸ2/∂x2 e2 + ∂ɸ3/∂x3 e3
ɸ = ∂ɸ/ ∂x1 e1 + ∂ɸ2/∂x2 e2 + ∂ɸ3/∂x3 e3
= ∂ɸ/∂xi ei = ∂ɸ/∂x. is important as it takes the dot product of 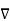 ɸ with dx it gives the increment in ɸ
ɸ with dx it gives the increment in ɸ
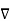 ɸ . dx = ∂ɸ/∂xi ei . dxj ej
ɸ . dx = ∂ɸ/∂xi ei . dxj ej
= ∂ɸ/∂xi . dxi = dɸ
= ɸ(x+dx) - ɸ(dx)
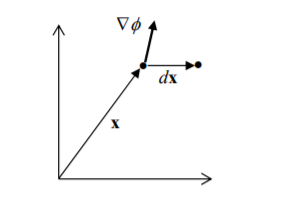
Figure Gradient of a vector
Properties:
The various properties of a gradient of a scalar field W are :
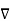
Q7) Explain divergence theorem?
Divergence theorem states that the volume integral of the divergence vector field is equal to the net outward flux of the vector through the closed surface that bounds the volume.
Mathematically 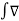
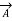 dv =
dv = 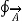
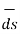
Let us consider a volume V enclosed by a surface S. Let us subdivide the volume in large number of cells. Let the kth cell has a volume ∆ Vk and the corresponding surface is denoted by Sk. Interior to the volume cells have common surfaces. Outward flux through these common surfaces from one cell becomes the inward flux for the neighbouring cells. Therefore, when the total flux from these cells are considered we actually get the net outward flux through the surface surrounding the volume. Hence, we can write
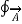
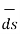 =
= 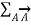
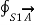
 =
= 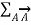
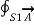
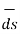 /
/ 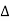 Vk . ∆ Vk
Vk . ∆ Vk
In the limit that is when k->∞ and ∆ Vk -> 0 the right hand of the expression can be written as
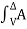 dv . Hence we get
dv . Hence we get 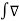
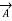 dv =
dv = 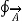
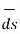
Q8) What is curl of vector?
Mathematically it is defined as
Curl of 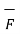 = lim ∆ SN ->0
= lim ∆ SN ->0 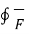 . d
. d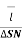
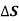 N = Area enclosed by the line integral in normal direction
N = Area enclosed by the line integral in normal direction
Thus, maximum circulation of 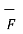 per unit area tends to zero whose direction is normal to the surface is called curl of
per unit area tends to zero whose direction is normal to the surface is called curl of 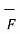 .
.
Symbolically it is represented as
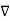 x
x 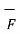 = curl of
= curl of 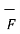
Q9) Explain Stoke’s theorem?
Stokes’ Theorem
For a simple region D with bounding curve C = ∂ D and two C’ function P and Q on D we have
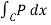 + Q dy =
+ Q dy = 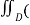 ∂Q/∂x - ∂P/∂y) dx dy
∂Q/∂x - ∂P/∂y) dx dy
Area of region is
A =
Q10) Explain Laplacian of scalar?
If V is a scalar field then the Laplacian of scalar V is denoted as 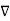 2 V and mathematically defined as the divergence of the gradient of V. The operator
2 V and mathematically defined as the divergence of the gradient of V. The operator
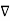 2 is called Laplacian operator.
2 is called Laplacian operator.
In cartesian co-ordinate system,
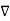 2 . V =
2 . V = 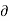 2 V /
2 V / 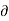 x 2 +
x 2 + 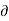 2 V /
2 V / 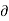 y 2 +
y 2 + 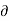 2 V /
2 V / 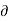 z 2
z 2
In cylindrical co-ordinate system
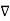 2 . V =
2 . V =  1/r
1/r 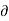 /
/ 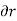 ( r
( r 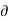 V/
V/ 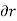 ) + 1/ r 2 (
) + 1/ r 2 ( 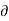 2 V /
2 V / 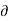 ɸ 2 ) +
ɸ 2 ) + 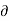 2 V /
2 V / 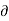 z 2
z 2