Electrostatic fields and Magnetostatic fields
Q1) Write a short note on electric field intensity?
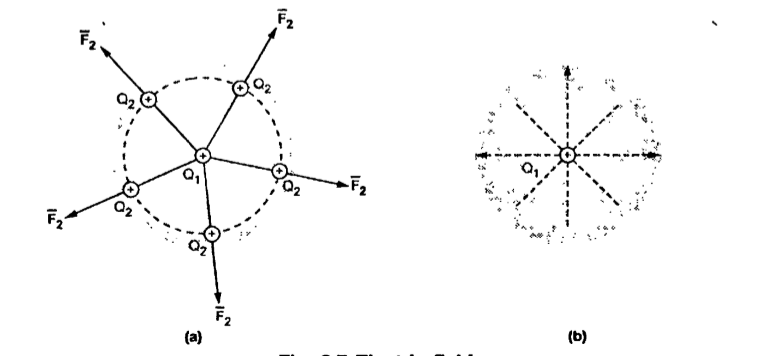
Consider a point charge Q1 as shown in figure:
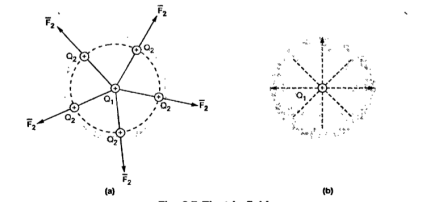
Figure . Electric field Intensity
If any other similar charge Q2 is brought near it Q2 experiences a force. Infact if Q2 is moved around Q1 still Q2 experiences a force as shown in figure.
Thus, there exists a region around a charge in which it exerts force on any other charge. This region where a particular charge exerts a force on any other charge located in that region called electric field of that charge . The electric field of Q1 is shown in figure (b).
The force experienced by the charge Q2 due to Q1 is given by Coulombs law as ,
 = Q1 Q2 / 4 π
= Q1 Q2 / 4 π  R2 12 .
R2 12 . 
Thus, force per unit charge can be written as:
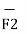 /Q2 = Q1 / 4 π
/Q2 = Q1 / 4 π  R2 12 .
R2 12 . 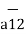
This force exerted per unit charge is called electric field intensity or electric field strength. It is a vector quantity and is directed along a segment from the charge Q1 to the position of any other charge.
It is denoted as 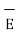 .
.
Another definition of electric field is the force experienced by a unit positive test charge that is Q2 = 1C.
Consider a charge Q1 as shown in figure below. The unit positive charge Q2=1C is placed at distance R from Q1. Then the force acting on Q2 due to Q1 is along the unit vector 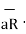 As the charge Q2 is unit charge the force exerted on Q2 is nothing but electric field intensity
As the charge Q2 is unit charge the force exerted on Q2 is nothing but electric field intensity 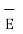 of Q1. Then the force acting on Q2 due to Q1 is along the unit vector
of Q1. Then the force acting on Q2 due to Q1 is along the unit vector 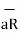 .As the charge Q2 is unit charge the force exerted onQ2 is nothing but electric field intensity
.As the charge Q2 is unit charge the force exerted onQ2 is nothing but electric field intensity 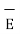 of Q1 at a point where unit charge is placed.
of Q1 at a point where unit charge is placed.
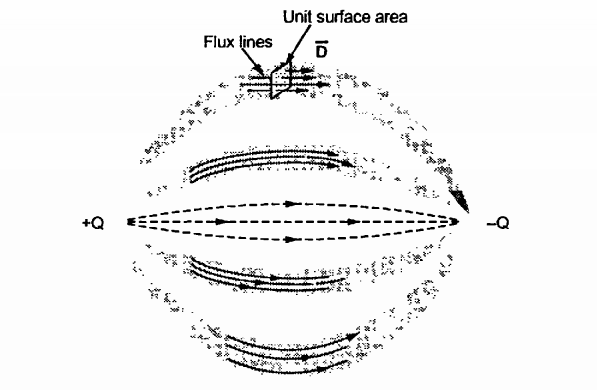
Q2) Write a short note on electric flux density?
Consider the two- point charges as shown in figure. The flux lines originating from positive charge and terminating at negative charge are shown in the form of tubes.
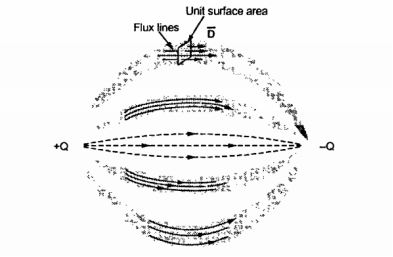
Figure . Electric flux density
Consider a unit surface area as shown in figure. Te number of flux lines are passing through this surface area.
The net flux passing normal through the unit surface area is called electric flux density. It is denoted as 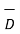 . It has specific direction normal to the surface area under consideration hence it is a vector field.
. It has specific direction normal to the surface area under consideration hence it is a vector field.
Consider a sphere with a charge Q placed at the centre. There are no other charges present around. The total flux distributes around the charge is 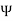 = Q. This flux distributes uniformly over the surface of the sphere.
= Q. This flux distributes uniformly over the surface of the sphere.
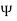 = Total flux
= Total flux
While S = Total surface area of sphere.
The electric flux density is defined as
D = 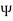 / S in magnitude.
/ S in magnitude.
Q3) Explain Gauss Law?
The electric flux passing through any closed surface is equal to the total charge enclosed by that surface.
The total charge enclosed by the irregular closed surface is Q coulombs. Hence the total flux has to pass through the closed surface is Q. Consider a small differential surface dS at point P. As the surface is irregular the direction of D as well as its magnitude is going from point to point on the surface. The surface dS under consideration can be represented in vector form.
d 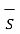 = d S
= d S 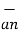
where 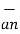 = Normal to the surface d at point P
= Normal to the surface d at point P
The flux density at point P is D and its direction is such that it makes an angle Ѳ with the normal direction at point P.
The flux d passing through the surface dS is the product of the component normal to dS and d
passing through the surface dS is the product of the component normal to dS and d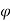 .
.
Mathematically thus can be represented as,
d 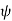 = Dn dS
= Dn dS
Dn = component of 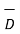 in the direction of normal to the surface dS
in the direction of normal to the surface dS
From the figure we can write
Dn = | | cos
| cos 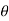
d 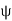 = |
= |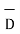 | cos
| cos 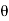 dS
dS
From the definition of the dot product
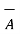 .
. 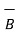 = |A| |B| cos ƟAB
= |A| |B| cos ƟAB
|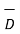 | cos
| cos 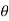 dS =
dS =  d
d 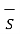
This is the flux passing through incremental surface area dS. Hence the total flux passing through the entire closed surface is to be obtained by finding the surface integration of the equation
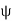 =
= 
 =
= 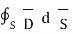
 sign indicates the integration over the closed surface called closed surface integral.
sign indicates the integration over the closed surface called closed surface integral.
Such a closed surface over which the integration in eq(6) is carried out is called Gaussian surface.
Total charge enclosed by the surface is given by
 =
=  = Q = Charge enclosed.
= Q = Charge enclosed.
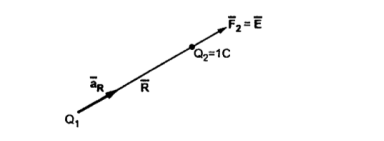
Figure . Concept of electric field intensity
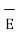 = Q1 / 4 π
= Q1 / 4 π 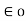 R2 .
R2 . 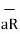
If a charge Q1 is located at the centre of the spherical coordinate system then unit vector 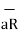 in equation (3) becomes the radial unit vector
in equation (3) becomes the radial unit vector 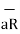 coming radially outwards from Q1 and the distance R is the radius of the sphere r.
coming radially outwards from Q1 and the distance R is the radius of the sphere r.
Q4) Write a short note on Maxwells equation?
The divergence of electric flux density  is given by
is given by
div 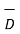 = lim ∆v->0
= lim ∆v->0  . d
. d 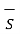 / ∆v --------------------(1)
/ ∆v --------------------(1)
 Dx/
Dx/ 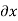 +
+  Dy /
Dy / 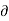 y +
y + 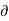 Dz/∂z -------------------------(2)
Dz/∂z -------------------------(2)
According to Gauss’s law it is known that
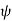 = Q =
= Q = 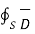 . d
. d  -----------------------------------------------(3)
-----------------------------------------------(3)
Expressing Gauss’s law per unit volume basis
Q/ ∆v = 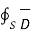 . d
. d 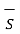 / ∆v -----------------------------------------(4)
/ ∆v -----------------------------------------(4)
Taking lim ∆v->0 volume shrinks to zero
lim ∆v->0 Q/ ∆v = lim ∆v->0 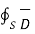 . d
. d 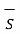 / ∆v
/ ∆v
But lim ∆v->0 Q/ ∆v = 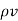 at that point-----------------------(5)
at that point-----------------------(5)
This equation gives the volume charge density at the point where divergence is obtained.
Equating (1) and (5)
div 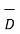 =
= 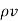 -------------------------------(6)
-------------------------------(6)
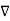 .
.  =
= 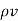
This is volume charge density around a point. The equation (6) is called Maxwells first equation.
Q5) Explain continuity time and relaxation time?
According to principle of charge conservation the time rate of decrease within a given volume must be equal to the net outward current flow through the closed surface of the volume.
The current Iout coming out of the closed surface
I out = 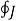 . dS = - d Qin/dt
. dS = - d Qin/dt
Where Qin is the total charge enclosed by the closed surface. Using diverhgence theorem
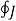 . dS =
. dS = 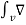 . J dv
. J dv
But
-d Qin/dt = -d/dt 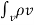 dv = -
dv = - 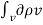 /dt dv--------------------(i)
/dt dv--------------------(i)
Equation (i) now becomes
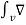 . J dv = -
. J dv = -  /dt dv
/dt dv
Or
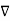 . J = - ∂
. J = - ∂ 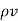 / ∂t
/ ∂t
This is called continuity of current equation.
According to Ohms law
J = 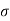 E
E
According to Gauss law
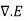 =
= 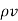 /
/  --------------------------------(ii)
--------------------------------(ii)
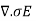 =
= 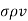 /
/  = - ∂
= - ∂ 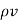 /
/ 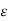
Or
∂ 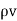 / ∂t +
/ ∂t + 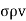 /
/ 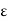 =0
=0
This is homogeneous linear ordinary differential equation. By separating variables, we get
∂ 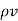 /
/ 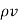 =
= 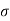 /
/ 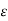 ∂t
∂t
Integrating both sides
ln 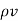 = -
= -  /
/  + ln
+ ln 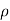 vo where
vo where 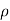 vo is constant of integration.
vo is constant of integration.
Where
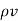 =
= 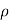 vo e -t/Tp
vo e -t/Tp
Tr = 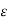 /
/ 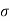
The time constant Tr is known as the relaxation time or the relaxation time.
Q6) Write a short note on boundary conditions?
When electric field passes from one medium to the other it is necessary to study the conditions at the boundary between two media. The conditions existing at the boundary of two media when field passes from one medium to the other are called boundary conditions.
Depending on the nature of the media there are two situations of boundary conditions:
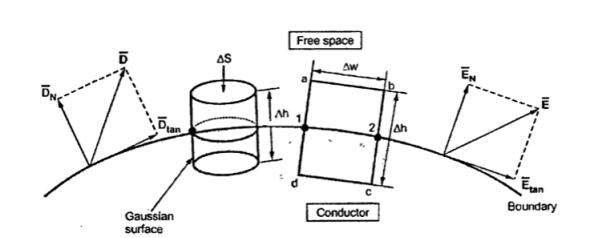
Figure 6. The boundary between conductor and free space.
Consider a boundary between conductor and free space. The conductor has infinite conductivity. For ideal conductor
The field intensity inside the conductor is zero and flux density inside a conductor is zero.
No charge can exist within a conductor. The charge appears on the surface in the form of surface charge density.
The charge density within the conductor is zero.
Thus 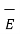 ,
, 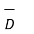 and
and 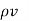 within the conductor
within the conductor  is zero is the surface charge density.
is zero is the surface charge density.
In order to determine the boundary conditions, use the closed path and Gaussian surface.
 at the boundary.
at the boundary.
Let 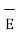 be the electric field intensity in the direction making some angle with the boundary. This
be the electric field intensity in the direction making some angle with the boundary. This  is resolved into two components
is resolved into two components
The component tangential to the surface
The component normal to the surface.
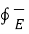 . d
. d 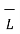 = 0 ------------------------(1)
= 0 ------------------------(1)
The integral 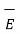 . d
. d 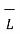 of carried over a closed contour is zero that is the work done in carrying unit positive charge along the closed path is zero.
of carried over a closed contour is zero that is the work done in carrying unit positive charge along the closed path is zero.
Consider a rectangular closed path abcda as shown in figure. It is traced in clockwise direction hence 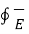 . d
. d 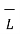 is divided into four parts:
is divided into four parts:
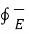 . d
. d  =
= 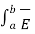 . d
. d 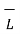 +
+ 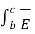 . d
. d 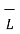 +
+ 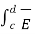 . d
. d 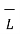 +
+ 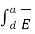 . d
. d 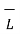 =0 ---------(2)
=0 ---------(2)
The closed contour is placed in such a way that its two sides a-b and c-d are parallel to tangential direction to the surface while the other two are normal to the surface at the boundary.
The rectangle with height 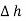 and width
and width  is placed in a manner that half of it is conductor and remaining half is free space. Thus
is placed in a manner that half of it is conductor and remaining half is free space. Thus 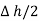 is in the conductor and
is in the conductor and 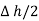
in free space.
The portion of c-d in conductor where 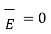 hence the corresponding integral is zero.
hence the corresponding integral is zero.
 . d
. d 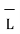 +
+ 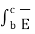 . d
. d 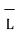 +
+ 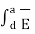 . d
. d 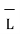 =0
=0
The width 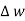 therefore E is constant hence,
therefore E is constant hence,
 . d
. d 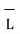 =
= 
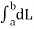 =
= 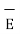
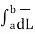 =
=  (
(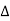 w) ---------------------(4)
w) ---------------------(4)
But 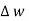 is tangential to the boundary hence
is tangential to the boundary hence 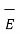 =
= 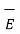 tan (∆w)
tan (∆w)
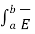 . d
. d 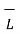 = E tan (∆w) where Etan = | E tan| ---------------(5)
= E tan (∆w) where Etan = | E tan| ---------------(5)
Now b-c is parallel to the normal component therefore 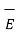 =
= 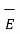 N along this direction. Let
N along this direction. Let
EN = |EN|
For small height 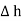 EN is assumed constant and taken out of integration.
EN is assumed constant and taken out of integration.
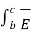 . d
. d  =
= 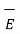
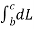 = EN
= EN 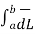 ----------------(6)
----------------(6)
But out of b-c , b-2 is in free space and 2-c is in the conductor when 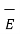 =0
=0
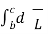 =
= 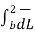 +
+  = ∆h/2 + 0 = ∆h/2 ----------------(7)
= ∆h/2 + 0 = ∆h/2 ----------------(7)
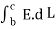 = EN (∆h/2) -------------------(8)
= EN (∆h/2) -------------------(8)
For path d-a the condition is same as for b-c only direction is opposite.
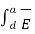 .
. 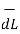 = -EN (∆h/2)
= -EN (∆h/2)
Substituting eq 4 and 8 and 3 and 9 we get
Etan ∆w + EN (∆h/2) - EN (∆h/2) = 0
Etan ∆w =0
E tan =0
Thus, the tangential component of the electric field intensity is zero at the boundary between conductor and free space.
Q7) A potential field is given as V = 100 e -5x sin 3y cos 4z V. Let point P (0.1,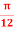 ,
, 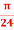 ) be located at a conductor free space boundary. At point P find the magnitudes of
) be located at a conductor free space boundary. At point P find the magnitudes of
a) V b) c) Et d) EN e)
c) Et d) EN e) 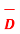 f) DN g)
f) DN g) 
At P , x=0.1 , y= 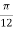 z =
z = 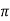 / 24.
/ 24.
V = 100 e – 0.5 sin 3 / 12 cos 4
/ 12 cos 4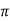 / 24 = 37.1422 V
/ 24 = 37.1422 V
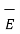 = -
= - 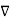 V ( ∂Vx/∂x
V ( ∂Vx/∂x 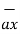 + ∂ Vy/ ∂ y
+ ∂ Vy/ ∂ y 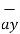 + ∂ Vz/ ∂ z
+ ∂ Vz/ ∂ z 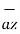
= -100[-5 e 5x sin 3y cos 4z 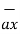 + e -5x (3) (cos3y)(cos 4z)
+ e -5x (3) (cos3y)(cos 4z) 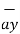 + e-5x (sin 3y) (4) (-sin 4z)
+ e-5x (sin 3y) (4) (-sin 4z) 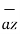
At P
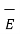 = [-100[-1.857
= [-100[-1.857 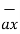 - 1.114
- 1.114 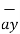 + 85.776
+ 85.776 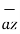 ]= 185.7
]= 185.7 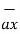 -111.4
-111.4 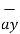 + 85.776
+ 85.776 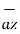
|E| = 232.9206 V/m
c ) Et = 0 V/m P is on the boundary.
d ) EN = | | = 232.9206 V
| = 232.9206 V
e ) 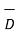 = 8.854 x 10 -12 [185.7
= 8.854 x 10 -12 [185.7 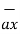 -111.4
-111.4  + 85.776
+ 85.776 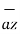 ]
]
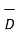 = 1.992 nC /m2
= 1.992 nC /m2
DN = | |= 1.992 nC /m2
|= 1.992 nC /m2
DN = 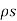 1.992 nC / m2
1.992 nC / m2
Q8) Explain Ampere’s Circuit law?
Gauss’s Law is useful to obtain 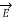 in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
It states that
The line integral of magnetic field intensity 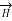 around closed path is exactly equal to direct current enclosed by that path.
around closed path is exactly equal to direct current enclosed by that path.
The mathematical representation of Ampere’s circuital law is
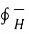 .
. 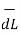 = I ----------------------------------(1)
= I ----------------------------------(1)
This law is useful to determine 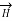 when current distribution is symmetrical.
when current distribution is symmetrical.
Proof:
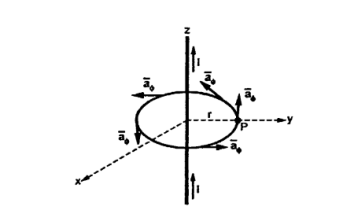
Figure . Conductor
Consider a long straight conductor carrying direct current I placed along z axis as shown in figure. Consider a closed circular path of radius r which encloses the straight conductor carrying direct current I. The point P is at perpendicular distance r from the conductor.
Consider 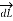 at point P which is direction
at point P which is direction 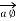 direction tangential to circular path at point P.
direction tangential to circular path at point P.
Therefore,
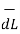 = r dɸ
= r dɸ  ------------------------------(2)
------------------------------(2)
While 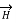 obtained at point P, from Biot-Savart law due to infinitely long conductor is,
obtained at point P, from Biot-Savart law due to infinitely long conductor is,
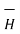 = 1/2πr .
= 1/2πr . 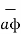 ---------------------------------(3)
---------------------------------(3)
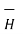 .
. 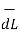 = 1/2πr .
= 1/2πr .  + r dɸ
+ r dɸ 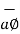
= 1/2πr . r dɸ = 1/2π dɸ
Integrating 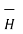 .
. 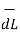 over the entire closed path
over the entire closed path
 .
. 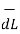 =
= 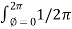 dɸ = 1/2π [ɸ] 0 2π
dɸ = 1/2π [ɸ] 0 2π
= I 2π/2π
This proves that the integral  .
. 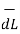 along closed path gives the direct current enclosed by that closed path.
along closed path gives the direct current enclosed by that closed path.
Steps to Apply Amper’s Circuital Law:
Step1: Consider a closed path preferably symmetrical such that it encloses the direct current I once. This is Amperian path.
Step2: Consider differential length 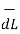 depending upon the co-ordinate system used.
depending upon the co-ordinate system used.
Step3: Identify the symmetry and find in which direction 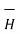 exists according to co-ordinate system used.
exists according to co-ordinate system used.
Step 4: Find 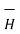 . Make sure that
. Make sure that 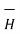 and
and 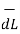 are in the same direction.
are in the same direction.
Step 5: Find the integral of 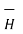 .
. 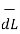 around the closed path. And equate it to current I enclosed by the path.
around the closed path. And equate it to current I enclosed by the path.
To apply Ampere’s circuital law the following conditions must be satisfied,
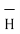

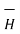
Q9) Explain magnetic scalar and vector potential?
In Electrostatics, electric field E is derivable from the electric potential V.
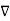 x E = 0
x E = 0
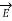 = -
= - 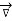 V
V
V is a scalar quantity and easier to handle than E which is a vector quantity. In Magnetostatics, the quantity Magnetic scalar potential can be obtained using analogues relation
 x B =
x B = 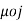
In regions of space in the absence of currents, the current density j =0
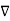 x B =0
x B =0
B is derivable from the gradient of a potential Therefore B can be expressed as the gradient of a scalar quantity φm B = - ∇φm φm is called as the Magnetic scalar potential.
The magnetic scalar potential is useful only in the region of space away from free currents. If J=0, then only magnetic flux density can be computed from the magnetic scalar potential The potential function which overcomes this limitation and is useful to compute B in region where J is present is . Magnetic Vector Potential.
Q10) Explain magnetic boundary conditions?

Figure . Charge density
Consider the electric displacement at a boundary between two different materials. To be completely general, we will assume that there is some surface charge density ρs (charge per unit area) on the boundary. Applying Gauss’ theorem to the divergence of the electric displacement, integrated over a pillbox crossing the boundary.
Take Maxwell’s equation: ∇ · D~ = ρ (1)
Integrate over the volume of the pillbox, and apply Gauss’ theorem:

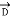 dV =
dV = 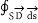 =
= 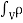 dV -------------------------------------------(2)
dV -------------------------------------------(2)
Taking the limit in which the height of the pillbox becomes zero. If the flat ends of the pillbox have (small) area A, then:
− D1nA + D2nA = ρsA
Dividing by the area A, we arrive at: D2n − D1n = ρ
Now consider the magnetic intensity at a boundary between two different materials
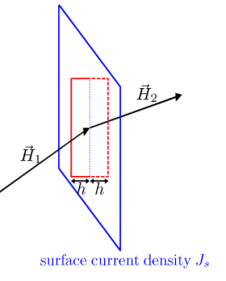
Figure . Current density
Assume that there is some surface current density J~s (current per unit length) on the boundary. On applying Stokes’ theorem to the curl of the magnetic intensity, integrated over a loop crossing the boundary.
Take Maxwell’s equation:
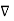 x
x 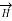 =
= 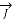 +
+ 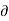
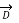 /
/ 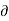 t ---------------------------------------------------(5)
t ---------------------------------------------------(5)
Integrate over the surface bounded by the loop, and apply Stokes’ theorem to obtain:
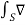 x
x 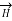 .
. 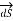 =
=  .
. 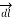 =
= 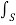 x
x  .
.  + ∂ / ∂t
+ ∂ / ∂t  .
.  ---------(6)
---------(6)
Now take the limit where the lengths of the narrow edges of the loop become zero:
where Js⊥ represents a surface current density perpendicular to the direction of the tangential component of H~ that is being matched
Boundary conditions on the normal component of the magnetic field B~ , and on the tangential component of the electric field E~ can be obtained using the same arguments.