Unit-3
Time domain analysis of Control System
Q1). The open-loop transfer function of a system with unity feedback gain G( S ) = 20 / S2 + 5S + 4. Determine the ξ, Mp, tr, tp.
Sol: Finding closed loop transfer function,
C( S ) / R( S ) = G( S ) / 1 + G( S ) + H( S )
As it is unity feedback so, H(S) = 1
C(S)/R(S) = G(S)/1 + G(S)
= 20/S2 + 5S + 4/1 + 20/S2 + 5S + 4
C(S)/R(S) = 20/S2 + 5S + 24
Standard equation for second order system,
S2 + 2ξWnS + Wn2 = 0
We have,
S2 + 5S + 24 = 0
Wn2 = 24
Wn = 4.89 rad/sec
2ξWn = 5
(a). ξ = 5/2 x 4.89 = 0.511
(b). Mp% = e-∏ξ / √1 –ξ2 x 100
= e-∏ x 0.511 / √1 – (0.511)2 x 100
Mp% = 15.4%
(c). tr = ∏ - φ / Wd
φ = tan-1√1 – ξ2 / ξ
φ= tan-1√1 – (0.511)2 / (0.511)
φ = 1.03 rad.
tr = ∏ - 1.03/Wd
Wd = Wn√1 – ξ2
= 4.89 √1 – (0.511)2
Wd = 4.20 rad/sec
tr = ∏ - 1.03/4.20
tr = 502.34 msec
(d). tp = ∏/4.20 = 747.9 msec
Q.2. A second order system has Wn = 5 rad/sec and is ξ = 0.7 subjected to unit step input. Find (i) closed loop transfer function. (ii) Peak time (iii) Rise time (iv) Settling time (v) Peak overshoot.
Sol: The closed loop transfer function is
C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
= (5)2 / S2 + 2 x 0.7 x S + (5)2
C(S)/R(S) = 25 / S2 + 7s + 25
(ii). tp = ∏ / Wd
Wd = Wn√1 - ξ2
= 5√1 – (0.7)2
= 3.571 sec
(iii). tr = ∏ - φ/Wd
φ= tan-1√1 – ξ2 / ξ = 0.795 rad
tr = ∏ - 0.795 / 3.571
tr = 0.657 sec
(iv). For 2% settling time
ts = 4 / ξWn = 4 / 0.7 x 5
ts = 1.143 sec
(v). Mp = e-∏ξ / √1 –ξ2 x 100
Mp = 4.59%
Q.3. The open loop transfer function of a unity feedback control system is given by
G(S) = K/S(1 + ST)
Calculate the value by which k should be multiplied so that damping ratio is increased from 0.2 to 0.4?
Sol: C(S)/R(S) = G(S) / 1 + G(S)H(S) H(S) = 1
C(S)/R(S) = K/S(1 + ST) / 1 + K/S(1 + ST)
C(S)/R(S) = K/S(1 + ST) + K
C(S)/R(S) = K/T / S2 + S/T + K/T
For second order system,
S2 + 2ξWnS + Wn2
2ξWn = 1/T
ξ = 1/2WnT
Wn2 = K/T
Wn =√K/T
ξ = 1 / 2√K/T T
ξ = 1 / 2 √KT
forξ1 = 0.2, for ξ2 = 0.4
ξ1 = 1 / 2 √K1T
ξ2 = 1 / 2 √K2T
ξ1/ ξ2 = √K2/K1
K2/K1 = (0.2/0.4)2
K2/K1 = 1 / 4
K1 = 4K2
Q.4. Consider the transfer function C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
Find ξ, Wn so that the system responds to a step input with 5% overshoot and settling time of 4 sec?
Sol:
Mp = 5% = 0.05
Mp = e-∏ξ / √1 –ξ2
0.05 = e-∏ξ / √1 –ξ2
Cn 0.05 = - ∏ξ / √1 –ξ2
-2.99 = - ∏ξ / √1 –ξ2
8.97(1 – ξ2) = ξ2∏2
0.91 – 0.91 ξ2 = ξ2
0.91 = 1.91 ξ2
ξ2 = 0.69
(ii). ts = 4/ ξWn
4 = 4/ ξWn
Wn = 1/ ξ = 1/ 0.69
Wn = 1.45 rad/sec
Q5) For the CLTF G(s) =  . Find Kp, Kv and Ka?
. Find Kp, Kv and Ka?
Sol: Kp = 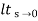 G(s)
G(s)
= 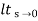
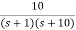
= 1
Kv =  SG(s)
SG(s)
=  S
S 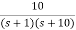
= 0
Ka = 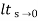 s2 G(s)
s2 G(s)
= 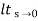 s2
s2 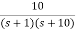
= 0
Q6) For a unity feedback system G(s) = 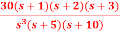 an input t3u(t) is applied. Find the steady-state error?
an input t3u(t) is applied. Find the steady-state error?
Sol: ess= 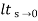
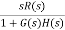
r(t) = t3u(t)
R(s) = 6/s4
H(s) =1
ess= 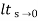
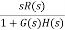
= 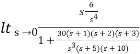
= 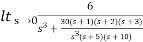
= 5/3
Q7) For the OLTF with unity feedback is G(s)=  . Determine the damping ratio, maximum overshoot, rise time?
. Determine the damping ratio, maximum overshoot, rise time?
Sol: The CLTF will be T(s) = 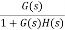
T(s) = 
For second order system,
S2 + 2ξWnS + Wn2
wn = 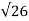 = 5.1
= 5.1
2ξWn = 5
i) Damping Ratio 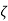 = 0.49
= 0.49
ii) Maximum overshoot Mp = e-∏ξ / √1 –ξ2 x 100
= e-∏x0.49 / √1 –(0.49)2
= 17.1%
iii) Rise Time tr = ∏ - φ/Wd
Wd = Wn√1 - ξ2
= 5.1 √1 – (0.49)2
= 4.45 sec
φ= tan-1√1 – ξ2 / ξ = 1.059 rad
tr = ∏ - φ/Wd
= ∏ - 1.059/4.45
=468.53msec
Q8) Define and derive the time domain specifications for a second-order system?
Sol:
1) Rise Time (tp):- The time taken by the output to reach the already status value for the first time is known as Rising time.
C(t) = 1-e-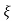 wnt/
wnt/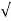 1-
1- 2 sin (wdt+ø)
2 sin (wdt+ø)
Sin (wd +ø) = 0
Wdt +ø = n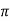
tr =n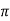 -ø/wd
-ø/wd
for the first time so,n=1.
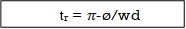
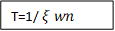
2) Peak Time (tp)
The peak value attained by the output is called peak time .The time required by the output to reach this value is lp.
d(cct) /dt = 0 (maxima)
d(t)/dt = peak value
tp = n /wd for n=1
/wd for n=1
tp = 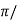 wd
wd
(3) Peak Overshoot Value
Maximum deviation of output from steady state value is called peak overshoot value(Mp ).
( ltp ) = 1 = Mp
(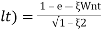 Sin(Wat + φ )
Sin(Wat + φ )
(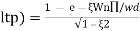 Sin( Wd∏/Wd + φ)
Sin( Wd∏/Wd + φ)
Mp = e-∏ξ / √1 –ξ2
Condition 3 ξ = 1
C( S ) = R( S ) Wn2 / S2 + 2ξWnS + Wn2
C( S ) = Wn2 / S(S2 + 2WnS + Wn2) [ R(S) = 1/S ]
C( S ) = Wn2 / S( S2 + Wn2 )
C( t ) = 1 – e-Wnt + tWne-Wnt
The response is critically damped.
(4). Settling Time (ts) :
ts = 3 / ξWn ( 5% )
ts = 4 / ξWn ( 2% )
Q9) Determine the type and order of the system G(s)= K/S(S+1)
G(S)= K(S+1)/S2(S+2)
Sol: G(s)= K/S(S+1)
It is order 2 and type 1 system
G(S)= K(S+1)/S2(S+2)
It is order 3 and type 2 system
Q10) Derive position error coefficient?
Sol: R(s)= Unit step
R(t) = u(t)
R(s) = 1/s
ess = 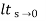 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 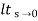 s[ys/1+G(s)]
s[ys/1+G(s)]
ess= 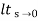 1+1/1+G(s)
1+1/1+G(s)
=1/1+lt G(s) s- 0

(Position error coefficient)