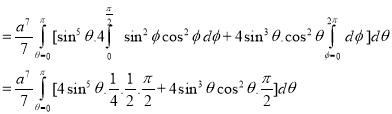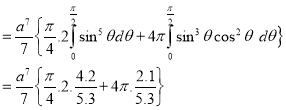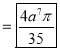Module 4
Multivariable Calculus-I
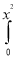
Soln. :
Given : I = 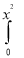 ey/x dy dx
ey/x dy dx
Here limits of inner integral are functions of y therefore integrate w.r.t y,
I = 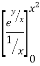
 dx
dx
= 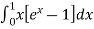
= 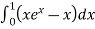
I = 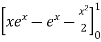
= =
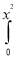 ey/x dy dx =
ey/x dy dx =
2. Evaluate x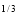 y
y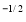 (1 – x –y)
(1 – x –y)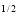 dx dy.
dx dy.
Soln. :
Given : I = x y
y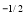 (1 – x –y)
(1 – x –y)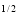 dx dy.
dx dy.
Here the limits of inner integration are functions of y therefore first integrate w.r.t y.
I = x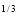 dx
dx 
Put 1 – x = a (constant for inner integral)
I = x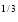 dx
dx 
put y = at dy = a dt
y | 0 | a |
t | 0 | 1 |
I = x dx
dx 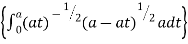
I = x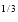 dx
dx 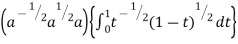
I = x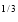 a dx
a dx
I = x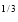 (1 – x) dx = (x
(1 – x) dx = (x – x4/3) dx
– x4/3) dx
I = 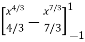
=
I = =
x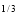 y
y (1 – x –y)
(1 – x –y)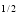 dx dy =
dx dy =
3. Evaluate 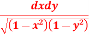
Soln. :
Let, I = 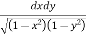
Here limits for both x and y are constants, the integral can be evaluated first w.r.t any of the variables x or y.
I = dy 
I = 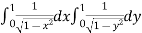
= 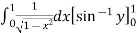
= 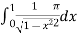
= 
=
= 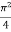
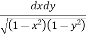 =
=
4. Evaluate e–x2 (1 + y2) x dx dy.
Soln. :
Let I = e–x2 (1 + y2) x dy = dy e–x2 (1 + y2) x dy
= dy e– x2 (1 + y2)  dx
dx
= dy [∵ f (x) ef(x) dx = ef(x) ]
= (–1) dy (∵ e– = 0)
= = =
e–x2 (1 + y2) xdx dy =
5. Evaluate y dx dy over the area bounded by x= 0 y = 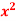 and x + y = 2 in the first quadrant
and x + y = 2 in the first quadrant
Soln. :
The area bounded by y = x2 (parabola) and x + y = 2 is as shown in Fig.6.2
The point of intersection of y = x2 and x + y = 2.
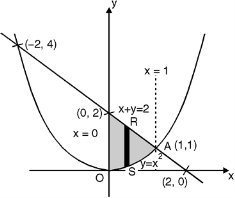
Fig. 6.2
x + x2 = 2 x2 + x – 2 = 0
x = 1, – 2
At x = 1, y = 1 and at x = –2, y = 4
(1, 1) is the point of intersection in the Ist quadrant. Take a vertical strip SR, Along SR x constant and y varies from S to R i.e. y = x2 to y = 2 – x.
Now slide strip SR, keeping IIel to y-axis, therefore y constant and x varies from x = 0 to x = 1.
I = 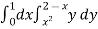
= 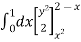
= 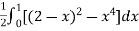
= (4 – 4x + 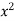 –
– 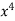 ) dx
) dx
= =
I = 16/15
6. Evaluate 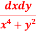 over x 1, y
over x 1, y 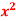
Soln. :
Let I =  over x 1, y
over x 1, y 
The region bounded by x 1 and y 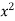
is as shown in Fig. 6.3.
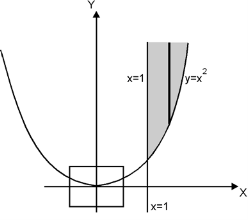
Fig. 6.3
Take a vertical strip along strip x constant and y varies from y = 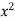
to y = . Now slide strip throughout region keeping parallel to y-axis. Therefore y constant and x varies from x = 1 to x = .
I = 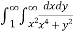
= 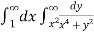
= 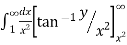 [ ∵
[ ∵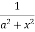 dx = tan–1 (x/a)]
dx = tan–1 (x/a)]
=  =
=
= – = (0 – 1)
I =
7. Evaluate (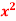 +
+  ) dx dy through the area enclosed by the curves y = 4x, x + y = 3 and y =0, y = 2.
) dx dy through the area enclosed by the curves y = 4x, x + y = 3 and y =0, y = 2.
Soln. :
Let I = (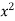 +
+ 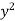 ) dx dy
) dx dy
The area enclosed by the curves y = 4x, x + y =3, y = 0 and y = 2 is as shown in Fig. 6.4.
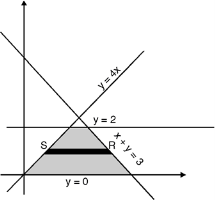
Fig. 6.4
(find the point of intersection of x + y = 3 and y = 4x)
Take a horizontal strip SR, along SR y constant and x varies from x = to x = 3 – y. Now slide strip keeping IIel to x-axis therefore x constant and y varies from y = 0 to y = 2.
I = dy (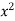 +
+ 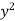 ) dx
) dx
= 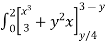
= 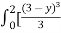 +
+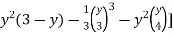 dy
dy
I = 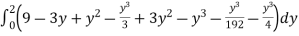
= 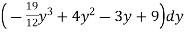
= 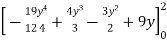
= + – 6 + 18
I =
8. Evaluate
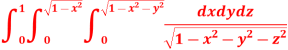
Solution: Let
I = 
= 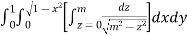
(Assuming m = 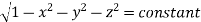 )
)
= 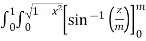 dxdy
dxdy
= 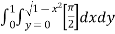
=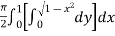
= 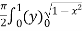 dx
dx
= 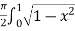 dx
dx
= 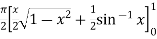
=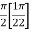
I =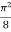
9. Evaluate 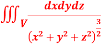 Where V is annulus between the spheres
Where V is annulus between the spheres 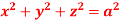
and  (
(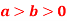 )
)
solution: It is convenient to transform the triple integral into spherical polar co-ordinate by putting
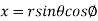 ,
, 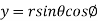 ,
, 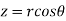
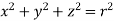 , dxdydz=
, dxdydz= sin
sin drd
drd d
d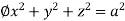 ,
,
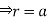 and
and 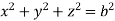
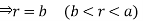
For the positive octant, r varies from r =b to r =a, 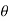 varies from
varies from 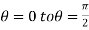
and 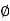 varies from
varies from 
I= 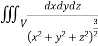
= 8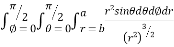
=8
=8
=8
=8 log
= 8 log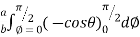
I= 8 log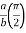 I = 4 log
I = 4 log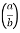
10. Evaluate 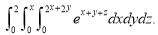
Solution:-
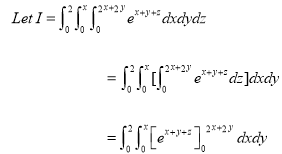



11. Evaluate 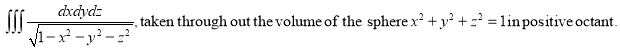
Solution:-
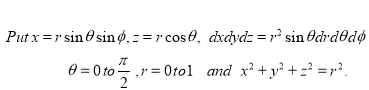

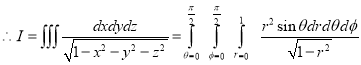

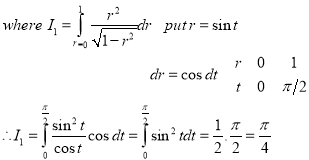

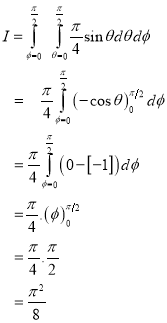
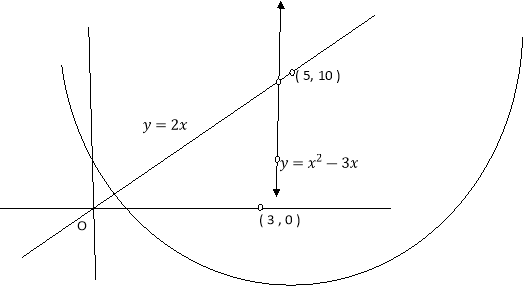
12. A lamina is bounded by the curves  and
and 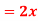 . If the density at any point is
. If the density at any point is  then find the mass of lamina.
then find the mass of lamina.
Solution:

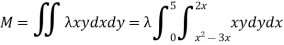
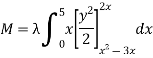
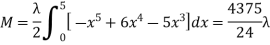
13. If the density at any point of a non-uniform circular lamina of radius’ a’ varies as its distance from a fixed point on the circumference of the circle then find the mass of lamina.
Solution:
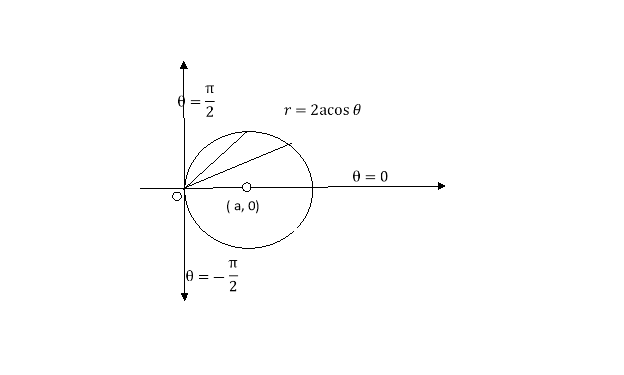
Take the fixed point on the circumference of the circle as origin and diameter through it as the x-axis. The polar equation of circle 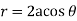
And density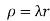 .
.
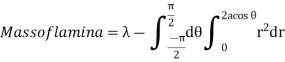
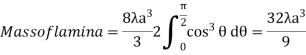
14. Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane
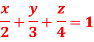
Solution: Volume =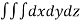 ………. (1)
………. (1)
Put 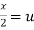 ,
, 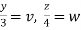
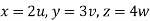
From equation (1) we have
V = 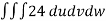
=24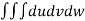
=24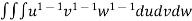 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 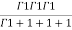
=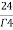 =
=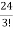 = 4
= 4
Volume =4
15. Find volume common to the cylinders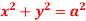 ,
, 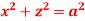 .
.
Solution: Forgiven cylinders,
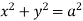 ,
, 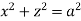 .
.
Z varies from
Z=-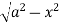 to z =
to z = 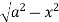
Y varies from
y= -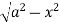 to y =
to y = 
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 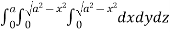
=8
= 8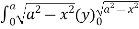 dx
dx
=8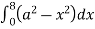
=8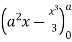
=8
Volume = 16
16. Evaluate
1. 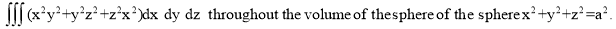 Solution:-
Solution:-