TOE
UNIT 4TORSIONQ 1) Explain Navier Theory of Torsion?A 1) The equation of motion also called the Navier equation for plane stress are given below-
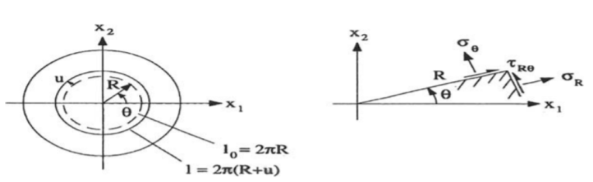
Figure: Circular plate with axis symmetrical displacementFig shows a circular slab having polar coordinate (R, Ɵ) it is axis symmetrical Hence radial displacement will be a function of R only- u=u(R). The stresses in polar coordinate are σ R ,τ RƟ and σ Ɵ but here shear stress will be zero because of axis symmetry and by Hooke’s Law the remaining stresses will be-
Q 2) Explain St. Venant’s Theory of Torsion/Semi- inverse method?A 2)
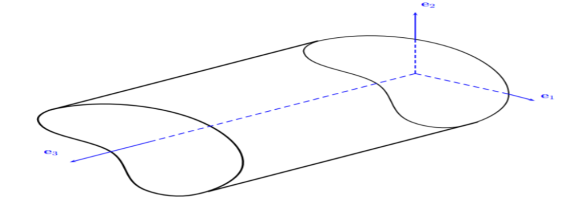
Figure Torsion of Prismatic barAssumptions –1. Each x3 =constant, rotation of the plane section like a rigid body about theCenter axis2. The rotation angle is a linear function of x 3To derive a St. Venant principle of torsion we apply a semi-inverse method according to this- (for axis symmetrical circular lab).It shows stress function gradient is perpendicular to the tangent and parallel with the normal boundary of the cross-section. it means Ø is constant over the cross-section boundary. For boundary value problem-Ø=0At the bar end (x 3 =0, L), the internal stresses are used to balance the external forces.Ignoring the details of how the external torque is appliedSimilarly for F2(A is cross-sectional area)-Here the Torque T should be – Where,First-term will be removed because Ø=0 at the boundaryQ 3) Write application of St. Venant Theory/Semi-inverse methodA 3)We use the following step to solve any bar having circular, elliptical, triangular, or rectangular cross-section.1. By solving the Poisson equation with boundary conditions we get a stressFunction.2. Obtain rate of twist from the equation
Where,First-term will be removed because Ø=0 at the boundaryQ 3) Write application of St. Venant Theory/Semi-inverse methodA 3)We use the following step to solve any bar having circular, elliptical, triangular, or rectangular cross-section.1. By solving the Poisson equation with boundary conditions we get a stressFunction.2. Obtain rate of twist from the equation 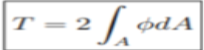 3. Compute strain and stresses.4. Compute raping functionQ 4) Explain Membrane Analogy?A 4)There are many cross-sections for which to find an analytical solution is very tough hence for these type of problem in 1903 Prandtl include an analogy which called membrane analogy in this analogy we take a thin membrane from the cross-section which have uniform pressure load as shown in figure-
3. Compute strain and stresses.4. Compute raping functionQ 4) Explain Membrane Analogy?A 4)There are many cross-sections for which to find an analytical solution is very tough hence for these type of problem in 1903 Prandtl include an analogy which called membrane analogy in this analogy we take a thin membrane from the cross-section which have uniform pressure load as shown in figure-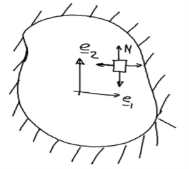 Figure: shows the membrane subjected to a uniform pressureIf N is membrane force per unit length and P is uniform pressure. Here the boundary condition will be u3 (x1, x 2 )=0, On comparing here we can get an analogy between membrane and torsion problem –
Figure: shows the membrane subjected to a uniform pressureIf N is membrane force per unit length and P is uniform pressure. Here the boundary condition will be u3 (x1, x 2 )=0, On comparing here we can get an analogy between membrane and torsion problem – Using the above analogy we can convert a complex membrane problem into a simple problem.Q 5) Write the formula of Venant’s Theory of Torsion?A 5) The formula of venants theory of torsion is given below:
Using the above analogy we can convert a complex membrane problem into a simple problem.Q 5) Write the formula of Venant’s Theory of Torsion?A 5) The formula of venants theory of torsion is given below:  Q 6) Write the formula of Prandtl’s Theory on Torsion?A 6) the formula of prandtl’s theory on torsion is given below:
Q 6) Write the formula of Prandtl’s Theory on Torsion?A 6) the formula of prandtl’s theory on torsion is given below: 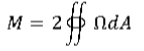 Q 7) Explain Saint-Venant’s Principle?A 7) “If the forces acting on a small portion of the surface of an elastic body are replaced by another statically equivalent system of forces acting on the same portion of the surface, this redistribution of loading produces substantial changes in the stresses locally, but has a negligible effect on the stresses at distances which are large in comparison with the linear dimensions of the surface on which the forces are changed.”Q 8) Explain torsion?A 8) Torsion: torsion defined as twisting of structural member when it is loaded by a couple (ie Equal and opposite forces) causing rotation of structural member about its longitudinal axis.Pure Torsion: A shaft of circular cross section is said to be in pure Torsion when it is subjected to equal and opposite end couple whose axis coincides with axis of shaft. Q 9) Explain assumption in torsion?A 9) Following are the assumptions made for the derivation of torsion equation:The material is homogeneous (elastic property throughout)The material should follow Hook’s lawThe material should have shear stress proportional to shear strainThe cross-sectional area should be planeThe circular section should be circularEvery diameter of the material should rotate through the same angleThe stress of the material should not exceed the elastic limitQ 10) Explain Power Transmission?A 10)One of the most common examples of torsion in engineering design is the power generated by transmission shafts. We can quickly understand how twist generates power just by doing a simple dimensional analysis. Power is measured in the unit of Watts [W], and 1 W = 1 N m s-1. At the outset of this section, we noted that torque was a twisting couple, which means that it has units of force times distance, or [N m]. So, by inspection, to generate power with a torque, we need something that occurs with a given frequency f, since frequency has the units of Hertz [Hz] or [s-1]. So, the power per rotation (2*pi) of a circular rod is equal to the applied torque times the frequency of rotation, or: P=2πFt = wT On the far right hand side of the equation, we've used the relation that angular velocity, denoted by the Greek letter omega, is equal to 2pi times the frequency.
Q 7) Explain Saint-Venant’s Principle?A 7) “If the forces acting on a small portion of the surface of an elastic body are replaced by another statically equivalent system of forces acting on the same portion of the surface, this redistribution of loading produces substantial changes in the stresses locally, but has a negligible effect on the stresses at distances which are large in comparison with the linear dimensions of the surface on which the forces are changed.”Q 8) Explain torsion?A 8) Torsion: torsion defined as twisting of structural member when it is loaded by a couple (ie Equal and opposite forces) causing rotation of structural member about its longitudinal axis.Pure Torsion: A shaft of circular cross section is said to be in pure Torsion when it is subjected to equal and opposite end couple whose axis coincides with axis of shaft. Q 9) Explain assumption in torsion?A 9) Following are the assumptions made for the derivation of torsion equation:The material is homogeneous (elastic property throughout)The material should follow Hook’s lawThe material should have shear stress proportional to shear strainThe cross-sectional area should be planeThe circular section should be circularEvery diameter of the material should rotate through the same angleThe stress of the material should not exceed the elastic limitQ 10) Explain Power Transmission?A 10)One of the most common examples of torsion in engineering design is the power generated by transmission shafts. We can quickly understand how twist generates power just by doing a simple dimensional analysis. Power is measured in the unit of Watts [W], and 1 W = 1 N m s-1. At the outset of this section, we noted that torque was a twisting couple, which means that it has units of force times distance, or [N m]. So, by inspection, to generate power with a torque, we need something that occurs with a given frequency f, since frequency has the units of Hertz [Hz] or [s-1]. So, the power per rotation (2*pi) of a circular rod is equal to the applied torque times the frequency of rotation, or: P=2πFt = wT On the far right hand side of the equation, we've used the relation that angular velocity, denoted by the Greek letter omega, is equal to 2pi times the frequency.
|
|
|
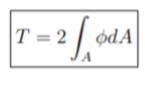 Where,First-term will be removed because Ø=0 at the boundaryQ 3) Write application of St. Venant Theory/Semi-inverse methodA 3)We use the following step to solve any bar having circular, elliptical, triangular, or rectangular cross-section.1. By solving the Poisson equation with boundary conditions we get a stressFunction.2. Obtain rate of twist from the equation
Where,First-term will be removed because Ø=0 at the boundaryQ 3) Write application of St. Venant Theory/Semi-inverse methodA 3)We use the following step to solve any bar having circular, elliptical, triangular, or rectangular cross-section.1. By solving the Poisson equation with boundary conditions we get a stressFunction.2. Obtain rate of twist from the equation 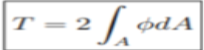 3. Compute strain and stresses.4. Compute raping functionQ 4) Explain Membrane Analogy?A 4)There are many cross-sections for which to find an analytical solution is very tough hence for these type of problem in 1903 Prandtl include an analogy which called membrane analogy in this analogy we take a thin membrane from the cross-section which have uniform pressure load as shown in figure-
3. Compute strain and stresses.4. Compute raping functionQ 4) Explain Membrane Analogy?A 4)There are many cross-sections for which to find an analytical solution is very tough hence for these type of problem in 1903 Prandtl include an analogy which called membrane analogy in this analogy we take a thin membrane from the cross-section which have uniform pressure load as shown in figure- Figure: shows the membrane subjected to a uniform pressureIf N is membrane force per unit length and P is uniform pressure. Here the boundary condition will be u3 (x1, x 2 )=0, On comparing here we can get an analogy between membrane and torsion problem –
Figure: shows the membrane subjected to a uniform pressureIf N is membrane force per unit length and P is uniform pressure. Here the boundary condition will be u3 (x1, x 2 )=0, On comparing here we can get an analogy between membrane and torsion problem – Using the above analogy we can convert a complex membrane problem into a simple problem.Q 5) Write the formula of Venant’s Theory of Torsion?A 5) The formula of venants theory of torsion is given below:
Using the above analogy we can convert a complex membrane problem into a simple problem.Q 5) Write the formula of Venant’s Theory of Torsion?A 5) The formula of venants theory of torsion is given below:  Q 6) Write the formula of Prandtl’s Theory on Torsion?A 6) the formula of prandtl’s theory on torsion is given below:
Q 6) Write the formula of Prandtl’s Theory on Torsion?A 6) the formula of prandtl’s theory on torsion is given below: 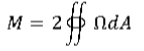 Q 7) Explain Saint-Venant’s Principle?A 7) “If the forces acting on a small portion of the surface of an elastic body are replaced by another statically equivalent system of forces acting on the same portion of the surface, this redistribution of loading produces substantial changes in the stresses locally, but has a negligible effect on the stresses at distances which are large in comparison with the linear dimensions of the surface on which the forces are changed.”Q 8) Explain torsion?A 8) Torsion: torsion defined as twisting of structural member when it is loaded by a couple (ie Equal and opposite forces) causing rotation of structural member about its longitudinal axis.Pure Torsion: A shaft of circular cross section is said to be in pure Torsion when it is subjected to equal and opposite end couple whose axis coincides with axis of shaft. Q 9) Explain assumption in torsion?A 9) Following are the assumptions made for the derivation of torsion equation:The material is homogeneous (elastic property throughout)The material should follow Hook’s lawThe material should have shear stress proportional to shear strainThe cross-sectional area should be planeThe circular section should be circularEvery diameter of the material should rotate through the same angleThe stress of the material should not exceed the elastic limitQ 10) Explain Power Transmission?A 10)One of the most common examples of torsion in engineering design is the power generated by transmission shafts. We can quickly understand how twist generates power just by doing a simple dimensional analysis. Power is measured in the unit of Watts [W], and 1 W = 1 N m s-1. At the outset of this section, we noted that torque was a twisting couple, which means that it has units of force times distance, or [N m]. So, by inspection, to generate power with a torque, we need something that occurs with a given frequency f, since frequency has the units of Hertz [Hz] or [s-1]. So, the power per rotation (2*pi) of a circular rod is equal to the applied torque times the frequency of rotation, or: P=2πFt = wT On the far right hand side of the equation, we've used the relation that angular velocity, denoted by the Greek letter omega, is equal to 2pi times the frequency.
Q 7) Explain Saint-Venant’s Principle?A 7) “If the forces acting on a small portion of the surface of an elastic body are replaced by another statically equivalent system of forces acting on the same portion of the surface, this redistribution of loading produces substantial changes in the stresses locally, but has a negligible effect on the stresses at distances which are large in comparison with the linear dimensions of the surface on which the forces are changed.”Q 8) Explain torsion?A 8) Torsion: torsion defined as twisting of structural member when it is loaded by a couple (ie Equal and opposite forces) causing rotation of structural member about its longitudinal axis.Pure Torsion: A shaft of circular cross section is said to be in pure Torsion when it is subjected to equal and opposite end couple whose axis coincides with axis of shaft. Q 9) Explain assumption in torsion?A 9) Following are the assumptions made for the derivation of torsion equation:The material is homogeneous (elastic property throughout)The material should follow Hook’s lawThe material should have shear stress proportional to shear strainThe cross-sectional area should be planeThe circular section should be circularEvery diameter of the material should rotate through the same angleThe stress of the material should not exceed the elastic limitQ 10) Explain Power Transmission?A 10)One of the most common examples of torsion in engineering design is the power generated by transmission shafts. We can quickly understand how twist generates power just by doing a simple dimensional analysis. Power is measured in the unit of Watts [W], and 1 W = 1 N m s-1. At the outset of this section, we noted that torque was a twisting couple, which means that it has units of force times distance, or [N m]. So, by inspection, to generate power with a torque, we need something that occurs with a given frequency f, since frequency has the units of Hertz [Hz] or [s-1]. So, the power per rotation (2*pi) of a circular rod is equal to the applied torque times the frequency of rotation, or: P=2πFt = wT On the far right hand side of the equation, we've used the relation that angular velocity, denoted by the Greek letter omega, is equal to 2pi times the frequency. 0 matching results found