Unit – 1
Definition of Fluid
Q1) Explain types of fluid with example.
A1) Fluids have common properties that they share, such as compressibility, density, pressure, buoyancy and viscosity.
Fluids are basically separated in 5 types
- Ideal fluid
- Real fluid
- Newtonian fluid
- Non–Newtonian fluid
- Ideal plastic fluid
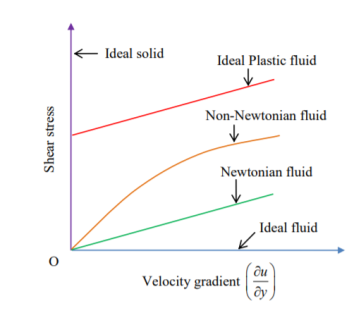
1. Ideal fluid – fluid which is incompressible in nature and no viscosity.in practical there is no ideal fluid, because all fluids have viscosity. Also called as imaginary fluid.
2. Real fluid - fluid which is compressible in nature and viscosity
Ex. Kerosene, petrol, castor oil.
3. Newtonian fluid – fluid which obeys Newton’s law of viscosity. In other words, fluids in which shear stress is directly proportional to rate of shear strain. This fluids viscosity totally depends on temperature and pressure of fluid.
Ex. Water, air, Hydrogen
4. Non –Newtonian fluid- fluid does not obey Newton’s law of viscosity. In other words, fluids in which shear stress is not directly proportional to rate of shear strain.
Ex – Flubber, Ooblek
5. Ideal plastic fluid - words fluids in which shear stress is directly proportional to rate of shear strain and in
Which shear stress is more than yield value.
Q2) What are properties of Fluids?
A2) There are various properties of fluid. Some of them are mentioned below:
- Mass Density
It is defined as the ratio of mass of the fluid to its volume. Its unit is kg/m3 and its dimensional formula is ML-3.
Density depends on temperature and pressure
2. Specific weight or weight density
Specific volume is defined as the ratio of volume of fluid to the mass of fluid.
It is denoted by Vs.
Mathematically it is denoted as
Vs=V/m=1/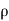
3. Specific Gravity
It can be defined as the ratio of specific weight of fluid to the specific weight of standard fluid.
It is unit less or dimensionless.
For liquid, the standard fluid is water and for gases the standard fluid is either H2
Or air at given temperature and pressure.
The specific gravity of water is 1.
If the specific gravity of liquid is less than 1 that means it is lighter than water and if the specific gravity of liquid is greater than 1, it means the liquid is heavier than water.
4. Compressibility
The measure of a liquid's relative volume change when the pressure acting on it varies is called compressibility.
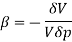
Where B = compressibilityV = Volume, P = Pressure
When a force acts on a fluid, it reduces its volume. The 'Bulk Modulus of Elasticity' is also used to assess this impact. The reciprocal of the Bulk Modulus of Elasticity can also be used to define the compressibility coefficient. The volume gets decreased when pressure increases so the negative sign.
5. Viscosity
It is the internal resistance offered by one layer fluid to the other layer.
Viscosity is the physic al property that characterizes the flow resistance of simple fluids.
Viscosity is the property of a fluid by virtue of its offer’s resistance to the movement of one layer of fluid over an adjacent layer.
Viscosity is also called as dynamic viscosity
Q3) Explain viscosity and kinematic viscosity.
A3) It is the internal resistance offered by one layer fluid to the other layer.
Viscosity is the physical property that characterizes the flow resistance of simple fluids.
Viscosity is the property of a fluid by virtue of its offer’s resistance to the movement of one layer of fluid over an adjacent layer.
Viscosity is also called as dynamic viscosity
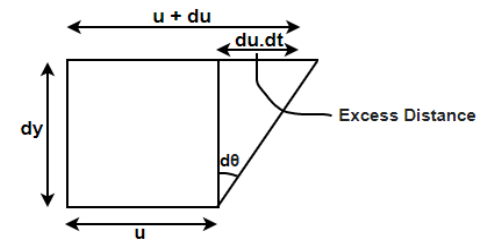
Figure: Viscosity diagram
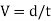
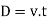
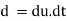
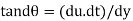
As the tandθ is very less, then
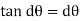
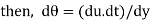
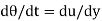
We know that, shear stress= shear force/shear area
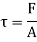
As the molecules are taken into same area:
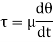
Kinematic viscosity
It is defined as the ratio of dynamic viscosity to the density of the fluid.it is also called as momentum diffusivity:

Where
 Kinmeatic viscosity
Kinmeatic viscosity
 Dynamic Visocosity
Dynamic Visocosity
 Density of the fluid
Density of the fluid
Q4) State Bernoulli’s theorem with application.
A4) It states that the sum of kinetic, potential and pressure heads of a fluid particle is constant along a streamline during steady flow when compressibility and frictional effects are negligible. i.e., For an ideal fluid, total head of fluid particle remains constant during a steady-incompressible flow.
Total head along a streamline is constant during steady flow when compressibility and frictional effects are negligible.
The total mechanical energy of the moving fluid comprising the gravitational potential energy of elevation, the energy associated with the fluid pressure and the kinetic energy of the fluid motion, remains constant.
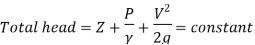
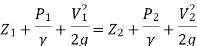
Applications of Bernoulli’s equation
Bernoulli’s equation is applied is all problems of incompressible fluid flow where energy considerations are involved, but we shall consider its applications to the following measuring devices:
- Venturi meter
- Pitot- tube
- Sub-merged orifice
- Orifice meters
- Rotameter.
Q5) What is pitot tube? How will you determine the velocity at any point with the help of pitot tube?
A5)
- It is a device used for measuring the velocity of flow at any point in a pipe or a channel.
- It is based on the principle, that if the velocity of flow at a point becomes zero, the pressure there is increased due to the conservation of the kinetic energy into pressure energy.
- In its simplest form, the pitot- tube consists of a glass tube, bent at right angles as shown in fig.
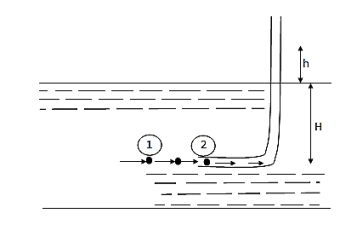
Fig.: Pitot tubes
- The Lower end, which is bent though 90° is directed in the upstream direction as shown in fig.
- The liquid rises up in the tube due to the conservation of kinetic energy into pressure energy.
- The velocity is determined by measuring the rise of liquid in the tube.
P1= intensity of pressure at point (1)
V1 = velocity of flow at (1)
P2 = pressure at point (2)
V2 = velocity at point (2), which is zero
H = depth of tube in the liquid.
h = rise of liquid in the tube above the fire Surface
Applying Bernoulli’s equation at points (1) and (2)
We get
P1/ W+V1 2 / 2 g +Z1=P2/ W+V22 / 2g+Z2
But Z 1 = Z2as points (1) and (2) are the same line and V2 =0
P1 /g= pressure Lead at (1) = H
P2 /g = pressure head at (2) = (h +H)
Substituting these values, we get
H+ V1 2 / 2 g = (h+H)
:. h= V1 2 / 2 g or v 1 = 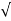 (2 g h)
(2 g h)
This is theoretical velocity.
Actual velocity is gives by (V 1) = Cv (2 g h)
(2 g h)
Where C v= Co-efficient of pitot-tube
:. Velocity at any point V= Cv (2 g h)
(2 g h)
Q6) What is surface tension?
A6) Surface tension is the tension of the surface film of a liquid caused by the attraction of the particles in the surface layer by the bulk of the liquid, which tends to minimize surface area.
Surface tension is a property of liquids that arises from unbalanced molecular cohesive forces at or near a surface.
Surface tension is the tendency of liquid surfaces to shrink into the minimum surface area possible. Surface tension allows insects (e.g., water striders), to float and slide on a water surface without becoming even partly submerged.
. 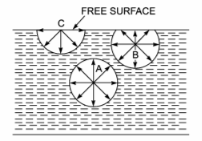
At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion).
There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract. Second is a tangential force parallel to the surface of the liquid. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane.
Surface tension has the dimension of force per unit length, or of energy per unit area. The two are equivalent, but when referring to energy per unit of area, it is common to use the term surface energy, which is a more general term in the sense that it applies also to solids.
S.I. Unit of Surface tension is N/m
The dimensional formula of surface tension is MT-2.
Examples of surface tension in action include the following:
--formation of liquid droplets,
--the ability of a needle to float on water,
--why bubbles are round
--soap being used the break up water tension.
Surface tension for various cases are
Sr | Case | Formula |
1 | Surface tension on liquid droplet | 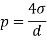 |
2 | Surface hollow tension on bubble |  |
3 | Surface hollow tension on liquid jet |  |
p is pressure intensity, d is diameter, 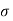 | ||
Q7) 2 liter petrol weighs 14 N. Calculate the specific weight, mass density, specific volume and specific gravity of petrol with respect to water. (2019-20)
A7)


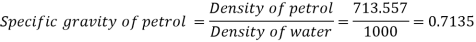

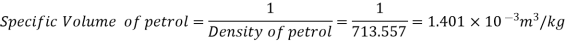
Q8) A plate 0.025 mm distant from a fixed plate moves at 1.4 m/sec and requires a shear stress of 2 N/m² to maintain this velocity. Find the viscosity of the fluid between the plates.
A8)
Let 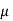 be viscosity,
be viscosity,
Shear stress, 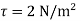
Velocity, V=1.4m/sec
Distance between plate y =0.025mm
Newton’s law of viscosity,
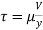
Or 
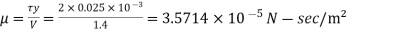
Q9) Find the surface tension in a soap bubble of 40 mm diameter when the inside pressure is 2.5 N/ m² above atmospheric pressure.
A9)
Given
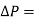 2.5 N/ m²,
2.5 N/ m²,
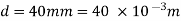
Because the soap film is incredibly thin, the soap bubble has two surfaces, one with air and the other with almost the same radius.

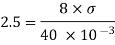

Q10) A venturimeter of 12 cm inlet diameter and 8 cm throat is laid horizontally in a pipe to measure the flow of oil of 0.9 specific gravity. The reading of a mercury manometer is 20 cm. Calculate the discharge in lit/min? The flow direction is upwards. The difference in elevation between inlet and throat is 30 cm. Determine the pressure head between inlet and throat. If coefficient of discharge is 0.97 calculate discharge.
A10)
Given
Inlet diameter 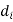 = 12cm =0.12m
= 12cm =0.12m
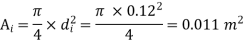
Throat diameter  = 8cm =0.08m
= 8cm =0.08m
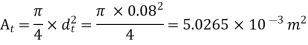
Difference in elevation, 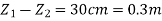
Coefficient of discharge, 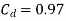
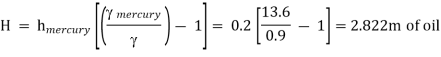
Theoretical Discharge is given by,
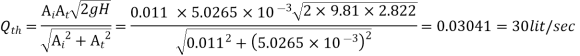
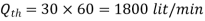
Pressure Head
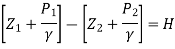
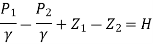
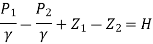
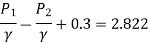
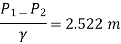
Actual Discharge is given by
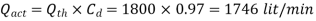
Q11) An orifice meter has an orifice of 10 cm diameter and a coefficient of discharge of 0.65. It is fixed in a pipe of 20 cm diameter with flowing oil of 0.8 specific gravity. The pressure difference between pipe and orifice is measured by a mercury manometer that gives a reading of 80 cm. Determine the discharge.
A11)
Given
Pipe diameter  = 20cm =0.2m
= 20cm =0.2m
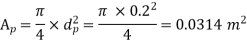
Orifice diameter 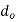 = 10cm =0.1m
= 10cm =0.1m
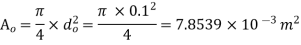
Coefficient of discharge, 

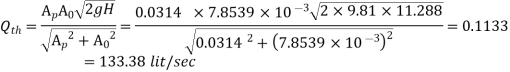
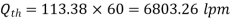
Actual Discharge is given by
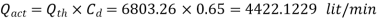
Q12) Water with a 10 m head is flowing through a 40 mm orifice. The discharge and velocity coefficients are 0.6 and 0.9, respectively. 1- What is the actual discharge from the orifice? 2- What is the actual vena contraction velocity?
A12)
Given
Orifice diameter 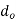 = 40mm =0.04m
= 40mm =0.04m
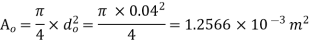
Theoretical Discharge from orifice

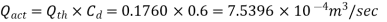

Actual vena contraction velocity
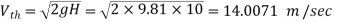
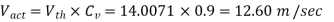
Q13) A hose is attached to a nozzle. The pressure in the entering section is 250 kPa, and the diameter is 20 mm. The diameter of the outlet section is 10 mm. The flow rate is 1.2 litres per second. Determine the amount of force required to keep the nozzle in place.
A13)
Given
Q=1.2 lit/s= 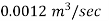
At entry, P1= 250 kPa, d1 =20mm
At exit, P2= 1 atm= 0, d2 =10mm
In x direction,
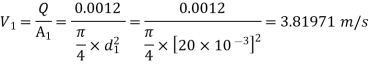
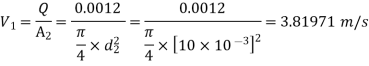
By momentum equation
Force in X direction
FT = FB + FW + FP = Q (vout – vin)
FB= Q (v2 – v1)- (P1 A1 + 0)
FB=1000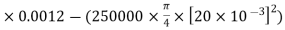 = -77.33N
= -77.33N
Force in Y direction
vout = vin = 0
The required holding force is -77.33N