Unit - 1

Review of Fundamental Concepts and Definitions

Q1) Assume a gas's specific heats at constant pressure and volume are Cp = 2,286 KJ/kg K and Cv = 1,768. Determine the molecular weight of a gas.

A1)

R = cp – cv = 0.518 kJ/kg.K

Molecular weight of gas = Universal gas constant/Characteristic gas constant = 8.3143/0.518

= 16.05 kg/k mol Ans.

Q2) It is possible to expand 750 kPa and 600 K perfect gas to 2 bar pressures. If the initial and final volumes of the gas are 0.2 m3 and 0.5 m3, calculate the final temperature of the gas.

A2)

Initial states = 750 × 103 Pa, 600 K, 0.2 m3

Final states = 2 bar or 2 × 105 Pa, 0.5 m3

Using perfect gas equation,

P1V1/T1 = P2V2/T2

T2 = 400 K

Final temperature = 400 K or 127º C Ans.

Q3) Determine the pressure of 5 kg carbon dixoide contained in a vessel of 2 m3 capacity at 27º C, considering it as

(i) perfect gas

(ii) real gas.

A3)

V = 2 m3, Universal gas constant. = 8.314 kJ/kg. K

T = 300 K

m = 5 kg

Considering it as perfect gas

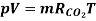
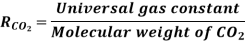
R = 8.314 *10 ^ 3 / 44.01 = 188.9 J/kg · K

P = 5* 188.9 *300 / 2 = 141675 N/m2

P = 1.417 × 105 N/m2

Considering it as real gas let us use Vander-Waals’s equation

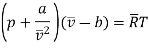
Vander Waals constant

Gas	Constant	Constant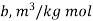
Helium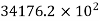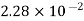
Hydrogen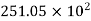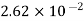
Oxygen	1392.5 ×	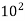3.14×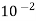
Air	1355.22×	3.62 ×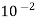
Carbon dioxide	3628.50×	3.14×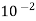
Gas	Constant	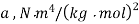Constant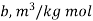

Where ‘v’ is molar specific volume and constants ‘a’ and ‘b’ can be seen from Table 1.6.

R = 8.314 × 103

Molar specific volume, = 2 * 44.01 / 5 = 17.604 m3/kg · mol

Vander-Waals Constant,

a = 3628.5 × 102 N . m4/(kg · mol)2

b = 3.14 × 10–2 m3/kg · mol

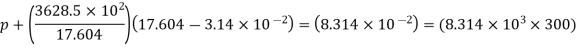
p = 140766.019 N/m2 = 1.408 × 105 N/m2

Q4) A steel insulated tank of 6 m3 volume is equally divided into two chambers using a partition. The two portions of tank contain N2 gas at 800 kPa and 480 K and CO2 gas at 400 kPa and 390 K. Determine the equilibrium temperature and pressure of mixture after removing the partition. Use γ = 1.4 for N2, γ =  1.3 for CO2.

A4)

Since tank is insulated so adiabatic mixing can be considered. Let us consider N2 and CO2 to behave as perfect gas.

No. Of moles of N2

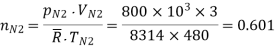
No of moles of CO2

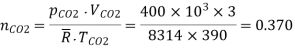
Total no. Of moles of mixture, = = 0.601 + 0.370 = = 0.971

Specific heat for 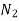at constant volume

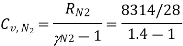
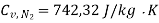
Specific heat for 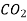at constant volume

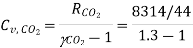
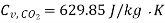
Mass of N2 = n N2 × Mol. Wt. Of N2 = 0.601 × 28 = 16.828 kg

Mass of CO2 = n CO2 × Mol. Wt. Of CO2 = 0.370 × 44 = 16.28 kg.

Applying energy conservation principle:

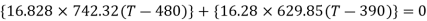
Equilibrium temperature, T = 439.4 K

Equilibrium pressure of mixture, Tmixture = 439.4 K, Vmixture = 6 m3

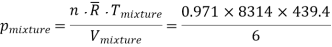
Equilibrium pressure = 591.205 kPa

Q5) A vessel of 2 m3 volume contains hydrogen at atmospheric pressure and 27ºC temperature. An evacuating pump is connected to vessel and the evacuation process is continued till its pressure becomes 70 cm of Hg vacuum.

Estimate the mass of hydrogen pumped out. Also determine the final pressure in vessel if cooling is carried up to 10ºC. Take atmospheric pressure as 76 cm of Hg and universal gas constant as 8.314 kJ/kg. K

A5)

For hydrogen, gas constant, R = 8.314 / 2 = 4.157 kJ/kg . K

Say initial and final states are given by ‘1’ and ‘2’.

Mass of hydrogen pumped out shall be difference of initial and final mass inside vessel.

Final pressure of hydrogen = Atm. Pr. – Vacuum pr.

= 76 – 70 = 6 cm of Hg.

Therefore, pressure difference = 76 – 6 = = 70 cm of Hg

= (70 / 76 )*  101.325 kPa

= 93.33 kPa

Mass pumped out =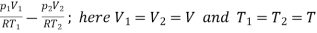

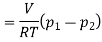
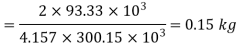
During cooling upto 10ºC, the process may be considered as constant volume process. Say the state before and after cooling are denoted by suffix 2 and 3.

Therefore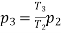

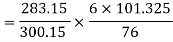
Final pressure after cooling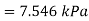

Q6) Determine the human body temperature in degree celsius (°C) if the temperature in Fahrenheit is 98.6°F.

A6)

Degree Celsius and Fahrenheit are related as below,

T (°C) = T (°F) – 32 / 1.8 = 98.6- 32 /1.8 = 37°C

Temperature in degree Celsius shall be 37°C.

Q7) In an unknown temperature scale freezing point of water is 0°X and boiling point of water is 1000°X. Obtain a conversion relation between degrees X and degree Celsius. Also determine the absolute zero in degree X.

A7)

Let the conversion relation be X = aC + b

Where C is temperature in degree celsius, a & b are constants and X is temperature in °X.

At freezing point, temperature = 0°C, 0°X

Or, 0 = a. 0 + b

⇒ b = 0

At boiling point, temperature = 100°C, 1000°X

1000 = a · 100 + b

⇒ a = 10

Conversion relation X = 10. C

Absolute zero temperature in °C = – 273.15°C

Absolute zero temperature in °X = – 2731.5°X

– 2731.5°X

Q8) Gas in cylinder is maintained at pressure of 689 kPa. Fluid expands from a volume of 0.04 m3 to 0.045 m3 while pressure remains constant. Paddle wheel in the system does a work of 4.88 kJ on the system. Determine (a) work done by system on the piston (b) the net amount of work done on or by the system.

A8)

a)     It is a closed system. If the pressure on face of piston is uniform, then the work done on piston

Can be obtained as,

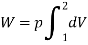
= 689 × 103 (0.045 – 0.04)

W = 3445 J or 3.445 kJ

Work done on piston = 3.445 kJ Ans.

b) Paddle work done on the system = – 4.88 kJ

Net work of system⇒ Wnet = Wpiston + Wpaddle = 3445 – 4880 = –1435 J

Work done on system = 1435 J or 1.435 kJ.

Work done on system = 1.435 kJ Ans.

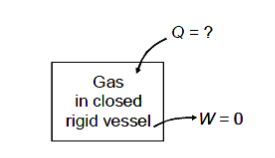
Q9) In a closed, rigid vessel, a gas at 65 kPa and 200°C is heated to 400°C. Assuming the internal energy at 200°C and 400°C is 26.6 and 37.8 kJ/kg, calculate the amount of heat necessary for 0.5 kg of the gas.

A9)

Given m = 0.5 kg

u1 = 26.6 kJ/kg

u2 = 37.8 kJ/kg

As the vessel is rigid therefore work done shall be zero.

W = 0

From first law of thermodynamics.

Q = U2 – U1 + W = m(u2 – u1) + 0

Q = 0.5 (37.8 – 26.6)

Q = 5.6 kJ

Heat required = 5.6 kJ Ans.

Q10) 50 kg/hr of carbon dioxide must be cooled from 800°C to 50°C by passing through a heat exchanger. Calculate the rate of heat removal assuming a constant and steady flow of gas. Think about cp = 1.08 kJ/kg K.

A10)

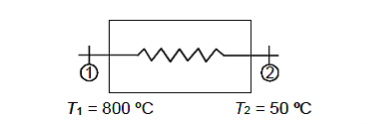
Given, m = 50 kg/hr

Writing down the steady flow energy equation.

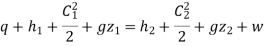
Here let us assume changes in kinetic and potential energy to be negligible. During flow the work

Interaction shall also be zero.

Hence q = h2 – h1

Or Q = m (h2 – h1)

= m · cp · (T2 – T1)

= 50 × 1.08 × (750)

= 40500 kJ/hr

Heat should be removed at the rate of 40500 kJ/hr Ans.

Q11) A 0.78 m3 cylinder is filled with air by opening its valve to the atmosphere and letting it fill up. Work done by air and environment on a system is determined.

A11)

Total work done by the air at atmospheric pressure of 101.325 kPa,

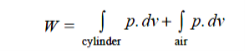
= 0 + p.Δv, it is –ve work as air boundary shall contract

Work done by air = – 101.325 × 0.78 = – 79.03 kJ

Work done by surroundings on system = + 79.03 kJ

Q12) A system consisting of a 5 kg gas is expanded from 1 MPa and 0.5 m3 to 0.5 MPa by means of a squeezing process. p.v1.3 = constant governs the expansion process. U = 1.8pv + 85kJ/kg is the formula for calculating the internal energy of a gas (u). In this case, "u" stands for the specific internal energy, "p" for the pressure, and "v" for the specific volume. Calculate heat and work interaction and internal energy change.

A12)

Given mass of gas, m = 5 kg, pv1.3 = constant

Assuming expansion to be quasi-static, the work may be given as,

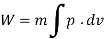
From internal energy relation, change in specific internal energy,

Δu = u2 – u1 = 1.8 (p2v2 – p1v1), kJ/kg

Total change, ΔU = 1.8 × m × (p2v2 – p1v1), kJ

ΔU = 1.8 × (p2V2 – p1V1)

Between states 1 and 2

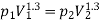
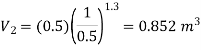
Total change in internal energy, ΔU = –133.2 kJ

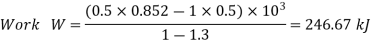
From first law,

ΔQ = ΔU + W

= –133.2 + 246.7

ΔQ = 113.5 kJ

Heat interaction = 113.5 kJ

Work interaction = 246.7 kJ

Change in internal energy = –133.2 kJ

Q13) A ideal gas with molecular weight 16 is compressed from 101.3 kPa at 20°C to 600 KPA using the law pV^1.3 = constant to determine the heat transfer and its direction. Take 1.7 kJ/kg.K as the specific heat at constant pressure of a gas.

A13)

Characteristic gas constant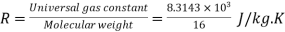

= 519.64, J/kg.K or = 0.51964, kJ/kg.K

R = 0.520, kJ/kg.K

Cv = Cp – R = 1.7 – 0.520

Cv = 1.18, kJ/kg.K

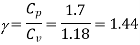
For polytropic process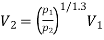

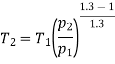
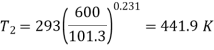
Work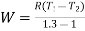

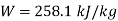
For polytropic process

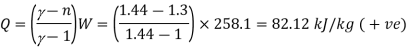
Q14) In a nozzle, air at 627°C and twice atmospheric pressure enters at negligible velocity and exits at 27°C. Determine the velocity of the air at the exit, assuming no heat loss and a horizontal nozzle. For air, use CP = 1.005 kJ/kg.K.

A14)

Applying steady flow energy equation with inlet and exit states as 1, 2 with no heat and work interaction and no change in potential energy.

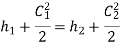
Given that 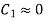negligible inlet velocity

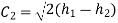
Exit velocity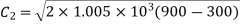 

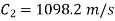
Exit velocity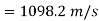

Q15) An air compressor requires 200 kJ/kg of air in shaft work, and compression increases the enthalpy of air by 100 kJ/kg of air. The cooling water required to cool the compressor absorbs heat at a rate of 90 kJ/kg of air. Calculate the heat transferred from the compressor to the atmosphere.

A15)

Work interaction, W = – 200 kJ/kg of air

Increase in enthalpy of air = 100 kJ/kg of air

Total heat interaction, Q = Heat transferred to water + Heat transferred to atmosphere.

Writing steady flow energy equation on compressor, for unit mass of air entering at 1 and leaving at 2.

Assuming no change in potential energy and kinetic energy.

Q = (h2 - h1 ) + W

= 100 + (- 200)

Q = - 100 kJ/kg of air

Q = - I 00 = Heat transferred to water + Heat transferred to atmosphere

So, - 100 = (- 90) + Heat transferred to atmosphere

Heat transferred to atmosphere = - 10 kJ/kg of air Ans.

Q16) Micro- or macro-scale studies of thermodynamics are possible. It's important to know the difference between macro and microscopical techniques. So, differentiate.

A16)

Studying thermodynamics can be done in two ways: macroscopic and microscopical. In the macroscopic approach, the state of matter is characterised b; defining just a few numbers of variables, and these variables can be measured and evaluated. Examples include a gas's pressure (P), temperature (7) and volume (V), all of which may be easily measured in order to define its state. The macroscopic method does not take into account the structure of the matter under investigation. The status of a gas can be seen here. Variables such as P, T and V can be used to characterise liquids and solids.

Atoms and molecules are minuscule particles that make up all stuff. The microscopic approach considers the structure of matter or the state of agglomeration, such as gas, liquid, or solid. These molecules move at random at independent speeds and there are intermolecular attractive and repulsive forces between them, making up matter. This is done by describing each atom or molecule’s position and velocity vectors, as well as the intermolecular forces that exist between them.

A vast number of variables are therefore necessary to characterise the state of matter when using the microscopic technique and these variables cannot be quantified. When assessing the behaviour of a substance, understanding its structure is vital.

Traditional thermodynamics uses a macroscopic approach while structural thermodynamics uses one that uses a microcosmic perspective.

Q17) Define a thermodynamic system and state its characteristics

A17)

Thermal systems are defined as discrete quantities of matter that are separated from the rest of the universe by a boundary and on which we focus our attention for thermodynamic analysis.

A system contains a specific amount of matter. This quantity does not change as the system goes through a process. Therefore. A system is also known as a control mass.

The boundary enclosing the system can be real, such as the glass wall of a thermos flask, or imaginary, such as the glass wall of a thermos flask acting as a boundary for enclosing coffee contained in the flask. For example, one could concentrate his attention on the air contained in the Im x Im x Im space of a room.

The system boundary can be rigid or change shape. As well as in size during a particular process That is, the volume of a system may change.

The system may exchange energy with its surroundings or with other systems in the form of work, heat, or both. An isolated system is one that does not exchange energy with its surroundings, both in the form of work and heat.

A system can be as simple as a specific amount of coffee held in a thermos flask or as complex as a massive petrochemical plant.

The selection of a system is not unique, and it is determined by the analyst.

Q18) What are the key characteristics of a thermodynamic property?

A18)

A thermodynamic property is a property that can be used to describe a system's state. The following are the essential characteristics of a property:

I. When a system is in a specific state, a thermodynamic property should have a definite value.

2. The change in the value of the property should not be affected by the system's path to the specified state. In other words, the change in the property is solely determined by the system's initial and final states. That is, the modification to the property Z can be written as

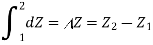
That is thermodynamic property is a point function or state function and it is not a path function. In other word, its differential is exact.

Note: if then

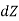is an exact differential if

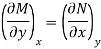
Q19) Explain

(a) kinetic energy

(b) potential energy

(c) mechanical energy

A19)

(a)  Kinetic energy: The energy possessed by a body by virtue of its motion is called the kinetic energy. If a body of mass of m moves with a velocity V the kinetic energy (KE) possessed by the body is given by

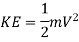
(b) Potential energy: The energy possessed by a body by virtue of its location or configuration is called potential energy. If a body of mass m is at an elevation of h above the datum plane. The potential energy (PE) possessed by the body is given by

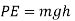
(c)  Mechanical energy.: The sum of the potential energy and Kinetic energy of a body is called the mechanical energy of the body.

Q20) Water can be cooled to a temperature (say, 10 o C) below its normal freezing point with care. The cold water produced in this manner is commonly referred to as super cooled water. Is the supercooled water in an equilibrium state?

A20)

Consider the Super' cooled water as a system and use the equilibrium criteria to determine whether it is in a state of equilibrium or not. The system has a uniform temperature, so it meets the thermal equilibrium criterion. Because the pressure is uniform throughout the system, the system also meets the mechanical equilibrium criterion. The system contains pure water that is at a constant temperature and pressure.

As a result, the chemical potential is consistent throughout the system. As a result, it also meets the criterion of chemical equilibrium. The system is in thermodynamic equilibrium because it meets the criteria of thermal, mechanical, and chemical equilibrium at the same time. When the system is subjected to a minor disturbance, such as the addition of a small amount of dust or the shaking of the container, the supercooled liquid immediately freezes into ice. As a result, the system is in metastable equilibrium.