Unit – 2
Second law of thermodynamics and Entropy
Q1) Using examples involving heat and work interactions, explain the limitations of the first law of thermodynamics.
A1)
We know that kinetic and potential energy are inextricably linked, and that the macroscopic modes of energy (KE and PE) can be easily converted into work. A heat engine is required to convert microscopic modes of energy (that is energy associated with the random molecular motion of the matter) or internal energy into work. Is it possible to convert all internal energy into work in a heat engine?
Is it possible to design a heat engine with an efficiency of one (defined as the ratio of net work done to energy absorbed)? Is it possible to spontaneously transfer energy as heat from a body at a lower temperature to a body at a higher temperature? All of the above questions concerning work and heat interactions cannot be answered using the first law of thermodynamics, and thus they reflect the limitations of the first law of thermodynamics.
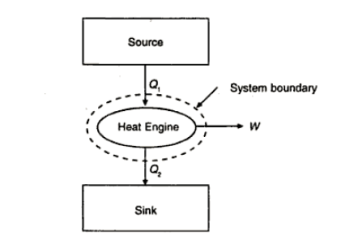
Q2) What is meant by a heat engine and what are its characteristics?
A2)
A heat engine is an energy conversion device. It is a cyclically operating device, and its primary objective is to convert the energy received as heat into work. It employs a working fluid which undergoes cyclic change. The working fluid absorbs energy as heat from a source and rejects energy as heat to a sink.
- It is a cyclically operating device.
- Its primary purpose is to convert energy absorbed as heat into work.
- It absorbs energy as heat from a high temperature source. It rejects energy as heat to a low temperature sink.
- It delivers some net work.
Q3) What is a heat pump or refrigerator and how the performance of these devices is evaluated?
A3)
A heat pump or a refrigerator is a device which works in a cycle. Absorbing energy as heat from a low temperature reservoir and rejecting energy as heat lo a high temperature reservoir when work is done on the device. Lf the objec1ivc of the device is to reject energy in the form of heat to a high temperature reservoir, it is called a heal pump. Heal pumps are generally used to keep the rooms warm in winter. On the other hand, if 1hc objective of the device is to extract energy in the form of heal from a low 1empera1ure body, it is called a refrigerator.
Usually, refrigerators are used to preserve food items and drugs at low temperature. In these devices Freon is usually used as a working fluid, and it is called as refrigerant. The index of performance of these devices is called the coefficient of perfom1ance. The coefficient of performance (COP) is defined as 1he ratio of the energy effect sought to the work done on the device. A schematic of a heat pump or refrigerator.
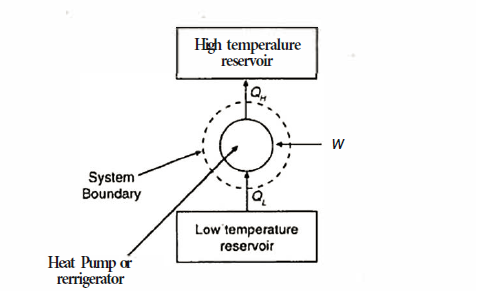
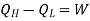
Where 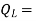 energy absorbed as heat from low temperature reservoir
energy absorbed as heat from low temperature reservoir
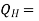 energy rejected as heat to the high temperature reservoir
energy rejected as heat to the high temperature reservoir
W= work done on the device
Then, the coefficient of performance in given by

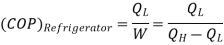

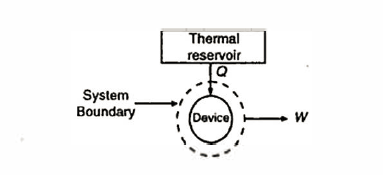
Q4) State the Kelvin- Planck statement of the second law of thermodynamics
A4)
The Kelvin-Planck statement of the second law of thermodynamics tells that it is impossible to devise a cyclically operating device which produces no other effect than the extraction of energy as heat from a single thermal-reservoir and delivers an equivalent amount of work. That is, it is impossible to devise a device.
Considering the working fluid as a system as shown application of the first law of thermodynamics gives Q = W. That is all the energy absorbed as heat by the device is completely converted into work. The Kelvin-Planck statement thus implies that no hear engine can have an efficiency equal to one.
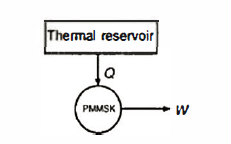
Q5) What is a perpetual motion machine of the second kind?
A5)
A Perpetual Motion Machine of the Second Kind (PMMSK) is a hypothetical device which operates in a cycle, absorbing energy as heat from a single thermal reservoir and delivering an equivalent amount of work.
The Kelvin - Planck statement of the second law of thermodynamics denies the possibility of devising a PMMSK. The PMMSK does not violate the first law of thermodynamics, but it violates the second law of thermodynamics.
Q6) State the Clausius statement of the second law of thermodynamics.
A6)
The Clausius statement of the second law of them1odynamics tells that it is impossible to devise a self-acting (that is unaided by any external agency) device which working cyclically, will produce no other effect than the transfer of energy is heat from a low temperature body to a high temperature body.
We know that 1he transfer of energy as heat from a high temperature body to a low temperature body occurs spontaneously. The Clausius statement of the second law of thermodynamics denies the possibility of self-reversal of such a spontaneous process. In other words, the second law of thermodynamics dictates the direction of a spontaneous process,
Thus, the second law of thermodynamics implies that the COP of a heat pump or refrigerator cannot be infinity.

Q7) Does the Clausius statement of the second law of thermodynamics prohibit the transfer of energy as heat from a body at low temperature to a body at high temperature? A domestic refrigerator absorbs energy as heat from the cold space and rejects energy as heat to the ambient atmosphere at a higher temperature. Does the refrigerator violate the second law of thermodynamics?
A7)
The Clausius statement of the second law of them1odynamics does not prohibit the transfer of energy as heat from a body at low temperature to a body at high temperature if the transfer of energy is externally aided. However. Spontaneous or externally unaided transfer of energy as heat from a low temperature body to a high temperature body is prohibited by the Clausius statement.
A domestic refrigerator does not violate the second law of thermodynamics, since work is done by an external agent on the refrigerator.
Q8) State Carnot theorem
A8)
The second law of thermodynamics leads lo several important consequences. The Carnot Theorems; are some of the consequences of the second law of thermodynamics. The Carnot theorems (proposed by Carnot) deal with the efficiency of a Carnot engine. The Carnot theorems are as follows
- No heat engine operating between the two given thermal reservoirs, with fixed temperatures. Can be more efficient than a reversible engine operating between the same two thermal reservoir.
- All reversible heal engines operating between the two given thermal reservoirs. With fixed temperatures, have the same efficiency. The efficiency of a reversible heat engine does not depend on the nature of the working fluid. But depends only on the temperatures of the reservoirs between which it operates.
Q9) Why is the thermodynamic temperature scale is also called absolute temperature scale?
A9)
The efficiency of a Carnot engine is given by
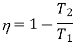
Since the efficiency of the heat engine cannot be greater than one, the lowest possible temperature on this scale is zero. Hence, the thermodynamic temperature scale is called absolute temperature scale.
Q10) Express the coefficient of performance of a Carnot heal pump and a Carnot refrigerator in terms of the temperatures of the thermal reservoirs between which they operate.
A10)

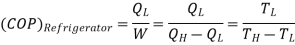

Q11) Determine the heat to be supplied to a Carnot engine operating between 400ºC and 15ºC and producing 200 kJ of work.
A11)
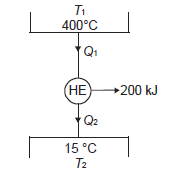
To find out 
In carnot engine from thermodynamic temperature scale;
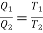 and work
and work 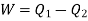
Thus 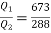
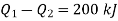
From equations 1 and 2, upon solving
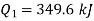
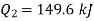
Heat to be supplied = 349.6 kJ
Q12) A refrigerator operates on reversed Carnot cycle. Determine the power required to drive refrigerator between temperatures of 42ºC and 4ºC if heat at the rate of 2 kJ/s is extracted from the low temperature region.
A12)
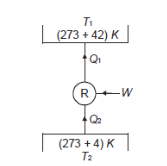
To find out, 
Given 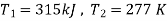
And 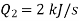
From the thermodynamic temperature scale,
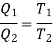
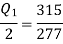
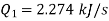
Power/work input required=
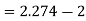
Power required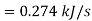
Power required for driving refrigerator=0.274 kW
Q13) A reversible heat engine operates between two reservoirs at 827ºC and 27ºC. Engine drives a Carnot refrigerator maintaining –13ºC and rejecting heat to reservoir at 27ºC. Heat input to the engine is 2000 kJ and the net work available is 300 kJ. How much heat is transferred to refrigerant and total heat rejected to reservoir at 27ºC?
A13)
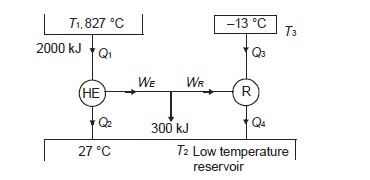
We can write, for heat engine, 
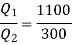
Substituting 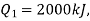 we get
we get 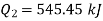
Also 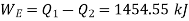
For refrigerator
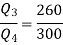
Also 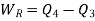
And 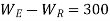
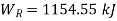
Equations (1) and (2) result in 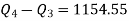
From equations (1) and (3)
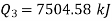
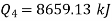
Total heat transferred to low temperature reservoir

Heat transferred to refrigerant=7504.58 kJ
Total heat transferred to low temperature reservoir =9204.68 Kj
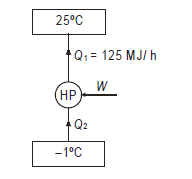
Q14) In a winter season when outside temperature is –1ºC, the inside of house is to be maintained at 25ºC. Estimate the minimum power required to run the heat pump of maintaining the temperature. Assume heating load as 125 MJ/h.
A14)
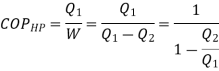
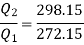
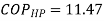
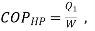 substituting
substituting 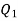
Therefore 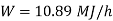
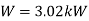
Minimum power required=3.02 kW
Q15) A cold storage plant of 40 tonnes of refrigeration capacity runs with its performance just ¼ th of its Carnot COP. Inside temperature is –15ºC and atmospheric temperature is 35ºC. Determine the power required to run the plant.
Take: One ton of refrigeration as 3.52 kW
A15)
Cold storage plant can be considered as a refrigerator operating between given temperatures limits.
Capacity of plant=Heat to be extracted=140.8 kW
Carnot COP of plant 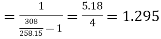
Actual 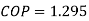
Also actual  , hence
, hence 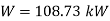
Power required=108.73 kW

Q16) What would be maximum efficiency of engine that can be had between the temperatures of 1150ºC and 27ºC?
A16)
Highest efficiency is that of Carnot engine, so let us find the Carnot cycle efficiency for given temperature limits.
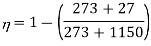
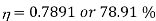
Q17) A domestic refrigerator maintains temperature of – 8ºC when the atmospheric air temperature is 27ºC. Assuming the leakage of 7.5 kJ/min from outside to refrigerator determine power required to run this refrigerator. Consider refrigerator as Carnot refrigerator.
A17)
Here heat to be removed continuously from refrigerated space shall be 7.5 kJ/min or 0.125 kJ/s.
Then, COP
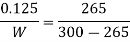
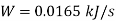
Power required =0.0165 kW

Q18) A Carnot engine getting heat at 800 K is used to drive a Carnot refrigerator maintaining 280 K temperature. Both engine and refrigerator reject heat at some temperature, T, when heat given to engine is equal to heat absorbed by refrigerator. Determine efficiency of engine and C.O.P. Of refrigerator.
A18)
Efficiency of engine
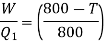
For refrigerator, COP
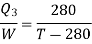
It is given that 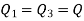
So from engine 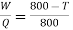
From refrigerator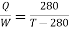
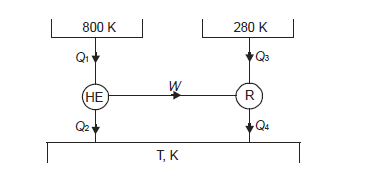
From above two 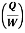 may be equated
may be equated
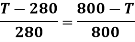
Temperature 
Efficiency of engine =
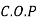 of refrigerator
of refrigerator 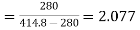
Q19) 0.5 kg of air executes a Carnot power cycle having a thermal efficiency of 50%. The heat transfer to the air during isothermal expansion is 40 kJ. At the beginning of the isothermal expansion the pressure is 7 bar, and the volume is 0.12 m3. Determine the maximum and minimum temperatures for the cycle in Kelvin, the volume at the end of isothermal expansion in m3, and the work and heat transfer for each of the four processes in kJ. For air cP = 1.008 kJ/kg. K, cv= 0.721 kJ/kg. K.
A19)
Given

Let thermodynamic properties be denoted with respect to salient states;
Carnot efficiency 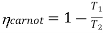
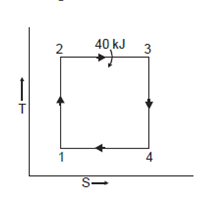

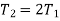
Corresponding to state 2, 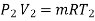
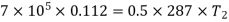
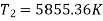
Heat transferred during process 2-3 (isothermal expansion) 
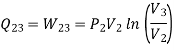
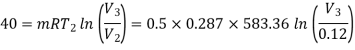
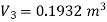
Temperature at state 1,
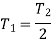
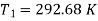
During process 1-2, 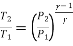
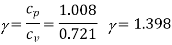

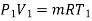
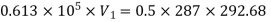
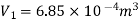
Heat transferred during process 4-1 (isothermal compression) shall be equal to the heat transferred during process 2-3(isothermal expansion)
For isoentropic process 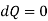
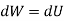
During process 1-2, isentropic process,
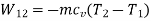
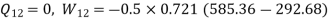
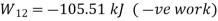
During process 3-4, isentropic process,
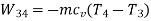

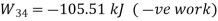
Process | Heat transfer | Work interaction
|
1-2 | 0 | -105.51 kJ |
2-3 | 40 kJ | 40k J |
3-4 | 0 | 105.51 kJ |
4-1 | -40kJ | -40 kJ |
Maximum temperature of cycle=585.36 kJ
Maximum temperature of cycle=292.68 kJ
Volume at the end of isothermal expansion=0.1932 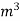
Q20) A reversible engine as shown in figure during a cycle of operation draws 5 mJ from the 400 K reservoir and does 840 kJ of work. Find the amount and direction of heat interaction with other reservoirs.
A20)
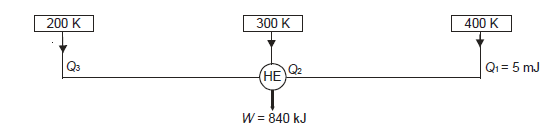
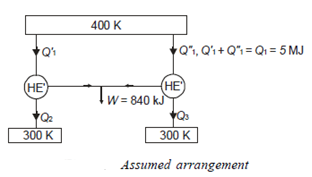
Thus 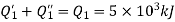
Also
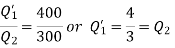
And
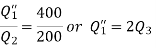
Substituting 
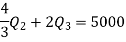
Also from total work output 
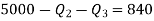


Substituting 
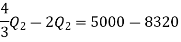
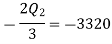
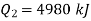
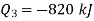
Negative sign with 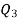 shows that the assumed direction of heat
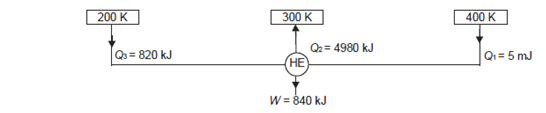
shows that the assumed direction of heat 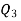 is not correct and actually
is not correct and actually 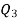 heat will flow from reservoir to engine. Actual sign of heat transfer and magnitudes are as under.
heat will flow from reservoir to engine. Actual sign of heat transfer and magnitudes are as under.
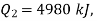 from heat engine
from heat engine
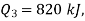 to heat engine
to heat engine