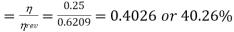Unit – 3

Availability and Irreversibility

Q1) Name the widely used thermodynamic potentials and define Helmholtz free energy and Gibbs free energy.

A1)

The widely used thermodynamic potentials are internal energy u, enthalpy h, Helmholtz free energy and Gibbs free energy g.

We know that

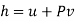
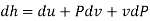
Substituting for du from eqn. (a) we get

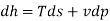
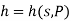
The Helmholtz free energy a is defined as

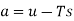
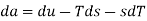
Substituting for du from eqn. (a) we get

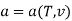
The gibbs free energy g is defined as

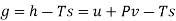
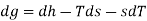
Q2) It is desired to compress air (an ideal gas with r = 1.4) in a piston-cylinder from I bar and 300 K to IO bar, with the final temperature of the air remaining at 300 K. The air interacts with the surrounding environment, which is also 300 K. Determine the smallest amount of work that must be done per mole of air.

A2)

The initial and final temperatures of the air are same as the surroundings temperature 300 K. The work done on the system will be minimum only when the process is reversible. The minimum work required is equal to the increase in the Helmholtz free energy of the system. That is

We also know that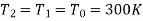

For an ideal gas (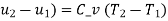

Since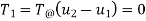

Therefore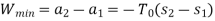

For an ideal gas

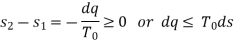
Therefore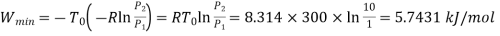

Q3) At 30 bar and 300°C, a piston cylinder assembly contains 0.1 kg superheated steam. This assembly is placed in thermal contact with a 300"C reservoir, and steam is allowed to expand to a pressure of 1 bar. Determine the maximum amount of work that can be obtained from steam.

A3)

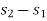
The initial and final temperatures of the steam are equal to the surrounding temperature, The maximum work can be obtained only if the process is reversible. The maximum work obtained is equal to the decrease in the Helmholtz free energy of the steam. That is

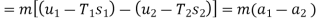
For steam at 30 bar and 300°C :

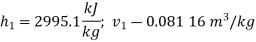
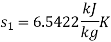
Therefore

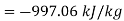
For steam at 1 bar and 300°C

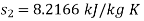
Therefore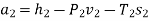

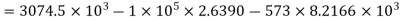
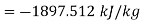
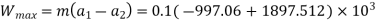
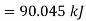
Q4) Why are the energy functions enthalpy and Gibbs free energy called as thermodynamic potentials?

A4)

Consider a device like turbine which is operating in steady state, steady• flow conditions through which material continuously flows in and flows out

Consider the device as the control volume and apply the first law of thermodynamics to the control volume to obtain

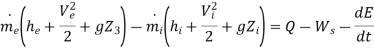
If the device is operating in steady – state, steady –flow conditions we have

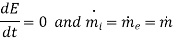
Suppose the device is adiabatic. Then

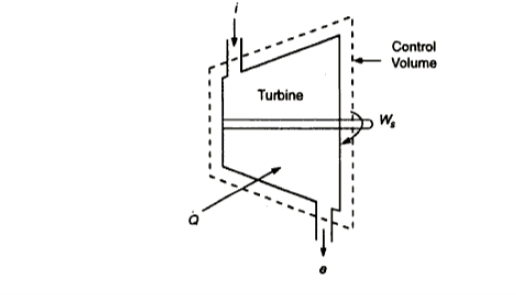
Ignore KE and PE changes. Then eqn(A) reduces to

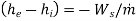
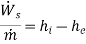
That is the power delivered per unit mass of fluid flowing through the device is equal to the decrease in the specific enthalpy of the fluid flowing through an adiabatic device. Therefore, enthalpy of the fluid the potential to do work and hence it is called a thermodynamic potential.

Now, consider a non-adiabatic device operating in steady-state, steady flow conditions. Ignore the KE and PE changes and apply the first law of thermodynamics to the device.

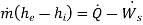
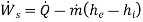
Suppose energy flows at a rate of Q from the surroundings at 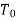into the control volume. The second law of thermodynamics gives

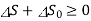
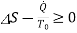  or  

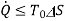
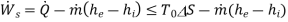
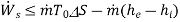
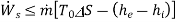
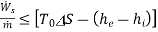  (D)

If the temperatures of the fluid at the inlet and outlet of the control-volume are equal to the surrounding temperature, that is

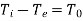
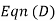reduces to

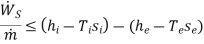
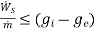   (E)

Thus, we find that the maximum work per unit mass that can be obtained from a device which is operating in steady- state, steady flow conditions such that the inlet and outlet temperatures of the fluid are same as that of the- surroundings, is equal to the decrease in the specific Gibbs free energy of the fluid flowing through the device. If there is any irreversibility in the device. The work that can be obtained per unit mass of the fluid is less than the decrease in the specific Gibbs free energy of the fluid.

If the device is an energy consuming device like compressor or pump. Then the minimum work required per unit mass of fluid flowing through it is equal to the increase in the Gibbs free energy of the fluid. If the inlet and outlet temperatures of the fluid are equal to the surroundings temperature. From this we observe that the Gibbs free energy represents the potential to do work and hence it is called a thermodynamic potential.

Q5) State the energy minimum principle

A5)

The energy minimum principle states that a system in a state of stable equilibrium will have the minimum internal energy few given values of entropy and volume. That is U is minimum for given values of Sand V or dU = O when S and V are held constant.

Q6) Define the intensive parameters in terms of thermodynamic potentials.

A6)

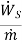
We know that

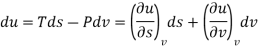
Therefore and

We know that

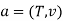
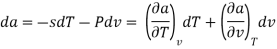
Therefore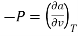

Q7) What is the importance of maxwell relation in thermodynamics?

A7)

The entropy plays an important role in the analysis of thermodynamic processes. Quite often one has to estimate the change in entropy of a syste associated with changes in the independent, measurable variables P, v and T. The entropy can be expressed in one of the following ways.

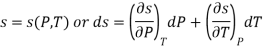
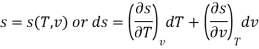
The entropy change can then be estimated by integrating the above relations. For this one should know the values of the six partial derivatives of entropy. Namely

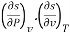 and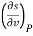

Of these, the partial derivatives of entropy with respect to temperature are measurable and are given by

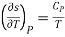and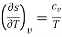

The remaining four partial derivatives of entropy wit respect to pressure and volume cannot be measured directly. The Maxwell relations express the partial derivatives of entropy with respect to pressure and volume I terms of measurable quantities, thus providing means for estimating the entropy change. The Maxwell relation obtained from the thermodynamic potential internal energy is given by [see Example 6.11]

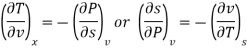
That is 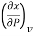is equal to the negative of the slope of v versus T curve for a reversible, adiabatic process which can be easily measured.

Q8) Derive the most used Maxwell relations standing from. The thermodynamic potentials expressed in terms of their natural variables.

A8)

The thermodynamic potentials are given by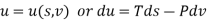 

Therefore we get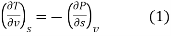

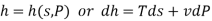
Therefore =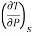

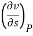
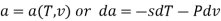
Therefore,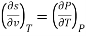

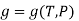  or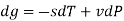 

Therefore 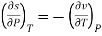  (2)

Equations (1) and (2) are the required Maxwell’s relations.

Q9) What is meant by second law efficiency and what is the necessity of introducing the term second law efficiency?

A9)

We know that the thermal efficiency or simply the efficiency of a heat engine cycle is defined as the ratio of the net work done to the energy absorbed. This efficiency is based on the conversion of energy supplied as heat into work and it is usually called as the first law efficiency because the first law of thermodynamics deals with the conservation of energy. Suppose a certain quantity of energy Q is available as heat at a higher temperature T1 while the ambient temperature is T0 Then the portion of Q which can be convened into work, or the available energy is given by

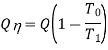
If the same amount of energy Q is available as heat at temperature then the available energy is given by

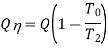
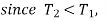we find that

That is, the available energy is high if the energy Q as heal is available at a higher temperature. Even though the lllllgni1ude of Q is identical, the potential or quality of Q is higher if it is available at higher temperature.

To consider the quality of energy, the term second law efficiency is introduced. The available energy depends on the entropy change of the source supplying the energy. Since the concept of en1ropy is based on 1he second law of 1herrnodynamics, the performance of a device in maintaining 1ht! available energy is expressed in terms of second law efficiency. The second law efficiency of a device is defined as

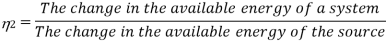
Q10) Deduce the Clausius-Clapeyron equa1ion from the Clapeyron equation.

A10)

Consider the liquid-vapor phase transi1ion al low pressures. Then the vapor phase may be approximated as an ideal gas. Moreover, the specific volume of the liquid is negligible compared to the specific volume of vapor (Vf << Vg) and hence

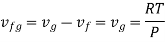
The clapeyron equation gives

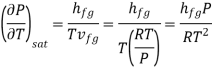
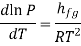
Which is known as the Clausius –Clapeyron equation

Q11) Steam enters a flow device at 1.6 MPa and 300oC with negligible velocity and exits at 0.1 MPa and 150oC with a velocity of 150 m/s. At 15oC, heat interaction with the surroundings occurs only during the flow, and the steam mass flow rate is 2.5 kg/s. Calculate the device's maximum possible output.

A11)

Let us neglect the potential energy change during the flow.

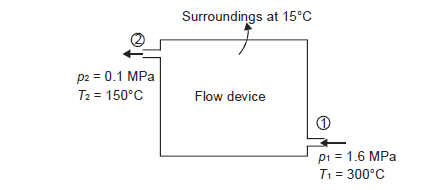
Applying S.F.E.E., neglecting inlet velocity and change in potential energy,

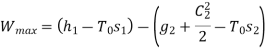
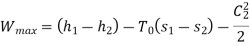
From steam tables

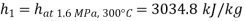
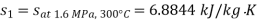
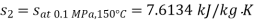
Given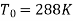 

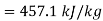
Maximum possible work=2.5×457.1 kJ/s=1142.75 kW

Maximum possible work=1142.75 kW

Q12) Two tanks A and B contain 1 kg of air at 1 bar and 50oC, and 3 bar and 50oC when the atmosphere is at 1 bar and 15oC. Determine which tank has the most stored energy. Find out how much air is available in each tank.

A12)

In these tanks the air stored is at same temperature of 50ºC. Therefore, for air behaving as perfect gas the internal energy of air in tanks shall be same as it depends upon temperature alone. But the availability shall be different.

Both the tanks have same internal energy

Availability of air in tank

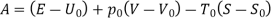
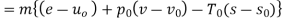
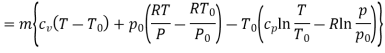
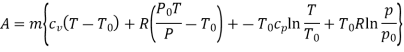
For tank A, 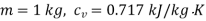, 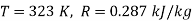K

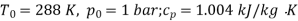
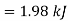
For tank B,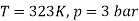

Availability of air in tank B is more than that of tank A

Availability of air in tank A=1.98kJ

Availability of air in tank B=30.98kJ

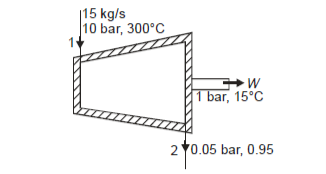
Q13) At 10 bar, 300oC, 15 kg/s steam enters a perfectly insulated steam turbine and exits at 0.05 bar, 0.95 dry with a velocity of 160 m/s. Assuming a 1 bar atmospheric pressure and a temperature of 15oC. Determine (a) power output, (b) maximum power for given end states, and (c) maximum power obtained from exhaust steam. The turbine rejects heat to a pond with 15oC water.

A13)

From steam tables, Enthalpy at inlet to turbine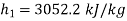

Enthalpy at exit of turbine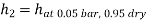

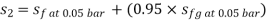
Similarly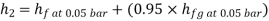

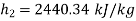
Neglecting the change in potential energy and velocity at inlet to turbine, the steady flow energy equation may be written as to give work output

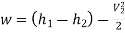
Power output=mw=15×598.06=8970.9 kW

Power output=8970.9 kW

Maximum work for given end states

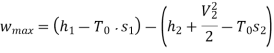
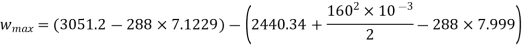
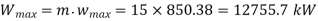
Maximum power output=12755.7 kw

Maximum power that could be obtained from exhaust steam shall depend upon availability with exhaust steam and the dead state. Stream availability of exhaust steam,

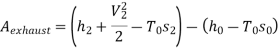
Approximately the enthalpy of water at dead state of 1 bar, 15°C can be approximated to saturated liquid at 15°C.

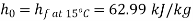
Maximum work available from exhaust steam

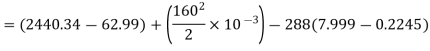
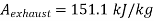
Maximum power that could be obtained from exhaust steam

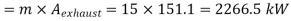
Q14) 5 kg of steam, initially at an elevation of 10 m and a velocity of 25 m/s, goes through some process to arrive at an elevation of 2 m and a velocity of 10 m/s. Determine the availability of the initial and final states. Estimate the change in availability assuming a temperature of 25oC and a pressure of 100 kPa in the environment. Thermodynamic properties u, v, s is as under.

Dead state of water

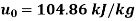
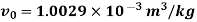
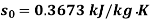
Initial state

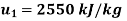
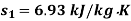
Final state

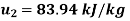
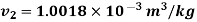
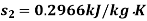
A14)

Availability at any state can be given by

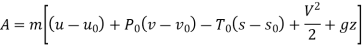
Availability at initial state

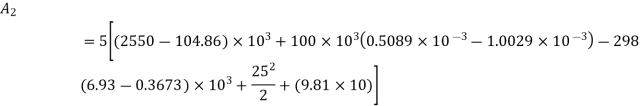
Availability at final state

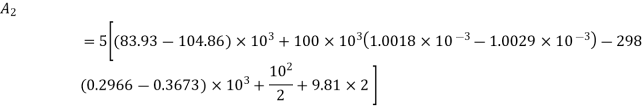
Availability at final stae=1.09 kJ

Change in availability:

Hence availability decreases by 2703.75 kJ

Q15) Exhaust gases from an internal combustion engine leave at 800oC and 1 atmosphere after performing 1050 kJ of work per kg of gas in engine. (Gas Cp = 1.1 kJ/kg K). The temperature outside is 30oC.

• How much available energy per kg of gas is lost by throwing away the exhaust gases?
• What is the ratio of the lost available exhaust gas energy to engine work?

A15)

Loss of available energy=Inversibility =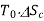

Here 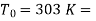Temperature of surroundings

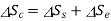
Change in entropy of system

Change in entropy of surroundings=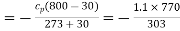

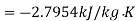
Loss of available energy=303(-2.7954+0.9786)

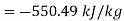
Ratio of lost available exhaust gas energy to engine work

Q16) 10 kg of water is transformed from an initial saturated vapour at 150oC with a velocity of 25 m/s and an elevation of 10 m to a saturated liquid at 20oC with a velocity of 10 m/s and an elevation of 3 m. Determine the availability for the initial state, final state, and change in availability when the environment is 0.1 MPa, 25oC, and g = 9.8 m/s2.

A16)

Let us consider velocities and elevations to be given in reference to environment. Availability is given by

Dead state of water,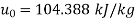

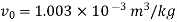
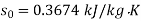
For initial state of saturated vapour at 150℃

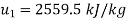
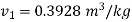
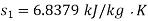
For final state of saturated vapour at 20℃

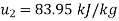
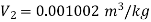
Substituting in the expression for availability

Initial state availability

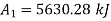
Final state availability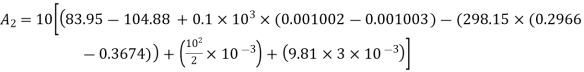

Change in availability, A=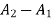

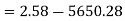
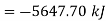
Initial availability =5650.28 kJ

Final availability=2.58 kJ

Change in availability=Decrease by 5647.70 kJ

Q17) A steam turbine has a steady rate of 5 kg/s of steam entering at 5 MPa and 500oC and leaving at 0.2 MPa and 140oC. At 1 atm and 25oC, a heat loss of 600 kJ/s occurs to the environment during flow through the turbine.

Determine

• The availability of steam at inlet to turbine,
• The turbine output
• The maximum possible turbine output, and
• The irreversibility

Neglect the changes in kinetic energy and potential energy during flow.

A17)

Let inlet and exit states of turbine be denoted as 1 and 2

At inlet to turbine

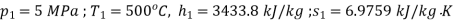
At exit from turbine

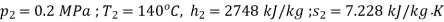
At dead state,

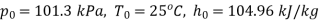
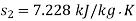
Availability of steam at inlet,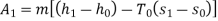

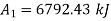
Availability of steam at inlet =6792.43kJ

Applying first law of thermodynamics

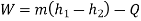
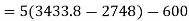
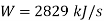
Turbine output =2829 kW

Maximum possible turbine output will be available when irreversibility is zero

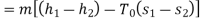
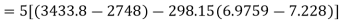
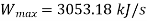
Maximum output =3053.18 kW

Inversibility can be estimated by the difference between the maximum output and turbine output

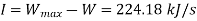
Inversibility=224.18 kW

Q18) 500 kJ of heat is removed from an 835 K constant temperature heat reservoir. A system receives heat at a constant temperature of 720 K. The temperature of the surroundings is 280 K, which is the lowest available temperature. Calculate the net loss of available energy due to irreversible heat transfer.

A18)

Here 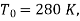ie surrounding temperature

Availability for heat reservoir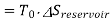

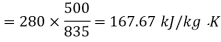
Availability for system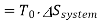

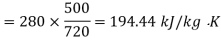
Net loss of available energy=(167.67-194.44)=-26.77 kJ/kg  K

Loss of available energy=26.77 kJ/kg  K

Q19) Describe the operation of an adiabatic steady flow turbine. The enthalpy at the entrance is 4142 kJ/kg and the enthalpy at the exit is 2585 kJ/kg. The flow availability of steam at the entrance and exit are 1787 kJ/kg and 140 kJ/kg, respectively, and the dead state temperature T0 is 300 K. Determine the actual work, the maximum possible work for the given change of state of steam, and the change in entropy of steam per kg of steam. Changes in kinetic and potential energy are ignored.

A19)

Here dead state is given as 300K and the maximum possible work for given change of state of steam can be estimated by the difference of flow availability as given under

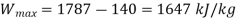
Actual work from turbine,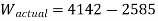

Actual work=1557 kJ/kg

Actual work=1557 kJ/kg

Maximum possible work-1647 kJ/kg

Q20) What is the second law efficiency of a heat engine with an efficiency of 0.25 and operating between reservoir temperatures of 500oC and 20oC?

A20)

Reversible engine efficiency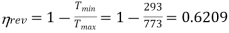

Second law efficiency