Unit – 4

Properties of steam and Rankine cycle

Q1) Derive the expression for Work of evaporation or external work of evaporation

A1)

This is the work done due to evaporation of water to steam as phase transformation from water to steam is accompanied by increase in volume. Work of evaporation can be estimated as; = p (vg – vf), for unit mass

For very low pressures of steam generation, where vf <<< vg. Work of evaporation = p·Vg

Work of evaporation for wet steam with dryness fraction ‘x’ = p ·x ·vg.

Q2) Write the expression for True latent heat

A2)

Latent heat causing the phase transformation from water to steam is accompanied with change in volume as well. Therefore, latent heat shall have two components i.e. (i) true latent heat causing phase change and (ii) work of evaporation due to volume increase. Mathematically, for unit mass, True latent heat = hfg – p(vg – vf).

Q3) Write the expression for Internal energy of steam

A3)

For a given mass of steam the total heat energy with steam can be said to comprise of

(i) Sensible heat

(ii) True latent heat

(iii) Work of evaporation

Out of above three the third component gets consumed in doing work. The internal energy of steam shall consist of first two components. For the enthalpy ‘h’ of steam,

(for unit mass) Internal energy, u = h – p(vg – vf) neglecting vf for low pressures,

For wet steam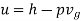

For superheated steam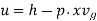

Hence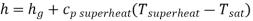

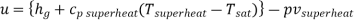
Q4) Write the expression for Entropy of water

A4)

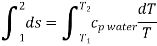
For constant specific heat of water

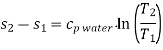
Absolute entropy may be given in reference to absolute zero temperature

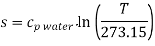
Q5) Write the expression for Entropy of evaporation

A5)

During evaporation heat absorbed is equal to latent heat of evaporation. Therefore, for unit mass

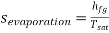
During incomplete evaporation (for wet steam)

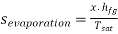
Q6) Write the expression for Entropy of wet steam

A6)

Entropy of wet steam=Entropy of water + Entropy of evaporation

For unit mass,

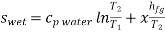
Q7) Write the expression for Entropy of super-heated steam

A7)

Entropy changes during constant pressure heating for superheating unit mass of the steam

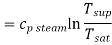
Total entropy of super heated steam, starting with water at temperature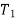

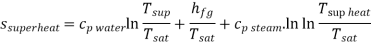
Q8) Steam enters the throttling calorimeter at 10 MPa and exits at 0.05 MPa and 100°C. Calculate the dryness fraction of steam.

A8)

During throttling,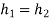

At state 2, enthalpy can be seen for super heated steam at 0.05 MPa and .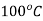

Thus

At state 1, before throttling

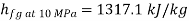
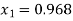
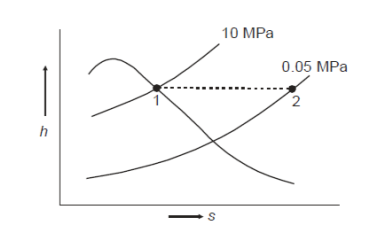
Dryness fraction is 0.968.

Q9) Calculate the internal energy of steam if its enthalpy, pressure, and specific volume are 2848 kJ/kg, 12 MPa, and 0.017 m3/kg, respectively.

A9)

Internal energy,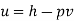

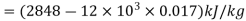
=2644 kJ/kg

Q10) At 2 MPa and 300°C, calculate the entropy of 5 kg of steam. Consider the specific heat of superheated steam to be 2.1 kJ/kg.K.

A10)

Steam state 2 MPa and 300℃ lies in super heated region as saturation temperature at 2 MPa is 212.42℃ and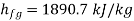

Entropy of unit mass of super heated steam with reference to absolute zero.

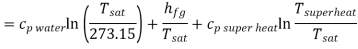
Substituting values

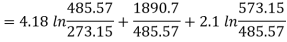
Entropy of 5 kg of steam=33.23 kJ/K

ENTROPY OF STEAM=33.23 kJ/K

Steam state 2MPa and 300℃ lies in super heated region as saturation temperature at 2 MPA

Q11) At what depth in the water does water in a pond boil at 110°C? What temperature should the water reach if we intend to boil it at 50 cm depth from the above-mentioned level?

A11)

Boiling point = 110°C, pressure at which it boils = 143.27 kPa (from steam table, sat. Pressure for 110°C)

At further depth of 50 cm the pressure

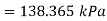
Boiling point at this depth=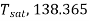

From steam table this temperature=108.866=108.87℃

Boiling point=108.87℃

Q12) A rigid vessel with a capacity of 0.5 m3 contains a water-vapour mixture at 100°C. Water is now heated until it reaches a critical temperature. What was the initial mass and volume of water?

A12)

In a rigid vessel it can be treated as constant volume process

Since final state is given to be critical state, then specific volume at critical point.

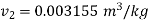
At 100℃ saturation temperature, from steam table

,

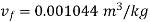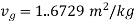
Thus for initial quality being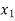

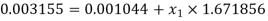
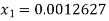
Mass of water initially=Total mass  (1-)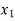

Total mass of fluid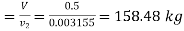

Mass of water =158.48 kg

Volume of water=158.48×0.001044

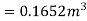
Mass of water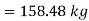

Volume of water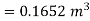

Q13) Determine slope of an isobar at 2 MPa and 500°C on mollier diagram.

A13)

On mollier diagram (h-s diagram) the slope of isobaric line may be given as

From 1st and IInd law combined

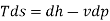
For constant pressure

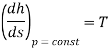
Here temperature

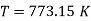
Hence slope =

Slope =773.15

Q14) Calculate the enthalpy, specific volume, and entropy of a 10% quality mixture at 0.15 MPa.

A14)

Given x=0.10

At 0.15 MPa, from steam table

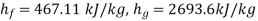
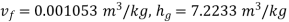
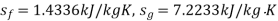
Enthalpy at x=0.1

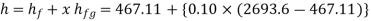
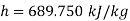
Specific volume,

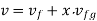
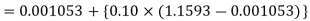
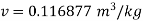
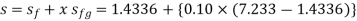
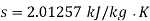
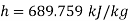
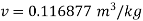
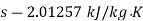
Q15) In a piston-cylinder arrangement, steam with a pressure of 1.0 MPa, an 80 percent dryness fraction, and a volume of 0.05 m3 is heated to a volume of 0.2 m3. Determine the amount of heat used.

A15)

Given

Initial states 1: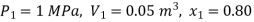

Final state, 2;

Work done during constant pressure process,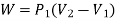

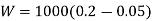
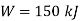
Mass of steam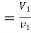

From steam table at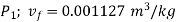

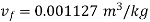
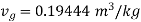
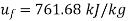
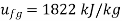
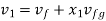
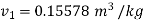
Hence mass of steam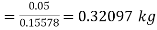

Specific volume at final state=

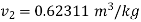
Corresponding to this specific volume the final state is to be located for getting the internal energy at final state at 1 Mpa

v2> vg1 Mpa

Hence state lies in superheated region, from the steam table by interpolation we get temperature as State lies between temperature of 1000°C and 1100°C.

So exact temperature at final state

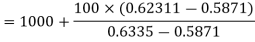
=1077.61℃

Thus internal energy at final state, 1 MPa, 1077.61℃

Internal energy at initial state

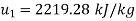
From first law of thermodynamics

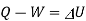
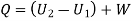
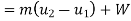
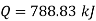
Heat added=788.83 kJ

Q16) Cooling will be used to condense steam at 800 kPa and 200°C in a rigid vessel. Determine the pressure and temperature associated with condensation

A16)

Here steam is kept in rigid vessel, therefore its specific volume shall remain constant.

Specific volume at initial state, 800kPa, 200℃C,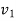

It is super heated steam as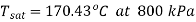

From  superheated steam table,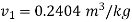

At the beginning of condensation, specific volume=0..2404

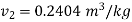
This 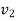shall be specific volume corresponding to saturated vapoure state for condensation.

Thus

Looking into steam table 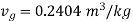shall lie between temperatures 175℃ () and 170℃ (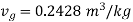) and pressures 892kPa (175℃ ) and 791.7 kPa (170℃ )

By interpolation, temperature at beginning of condensation

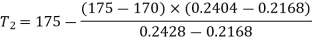
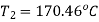
Similarly, Pressure,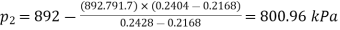

Pressure and temperature at condensation=800.96 kPa and 170.46℃

Q17) A feed water pump is used to pump water from 30°C to 200 kPa at a pressure of 200 kPa. Calculate the change in enthalpy assuming that water is incompressible, and that pumping is an isentropic process.

A17)

From Ist and IInd law:

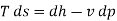
For isentropic process,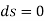

Hence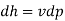

Ie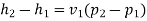

Corresponding to initial state of saturated at 30℃; from steam table;

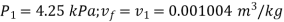
Therefore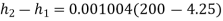

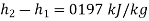
Enthalpy change=0.197 kJ/kg

Q18) A rigid vessel contains a liquid-vapour mixture in a 3:2 volume ratio. If the volume of the vessel is 2 m3 and the initial temperature is 150°C, calculate the quality of the water vapour mixture and total mass of fluid in the vessel.

A18)

From steam table at 150℃,

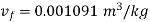
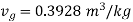
Volume occupied by water-1.2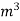

Volume of steam-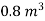

Mass of water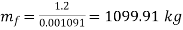

Mass of steam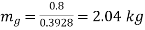

Quality or Dryness fraction,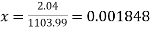

Mass=1103.99 kg, Quality=0.001848

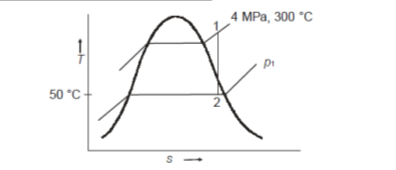
Q19) The steam turbine expands steam reversibly and adiabatically from 4 MPa and 300°C to 50°C at the turbine exit. Calculate the work output per kilogramme of steam.

A19)

From SFEE on steam turbine:

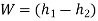
Initially at 4 MPa, 300℃ the steam is super heated so enthalpy from super heated steam table or Mollier diagram

Reversible adiabatic expansion process has entropy remaining constant. On Mollier diagram the state 2 can be simply located at intersection of constant temperature line for 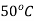and isentropic expansion line.

Else from steam tables at 50℃ saturation temperature:

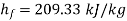
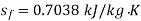
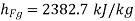
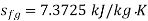
Here 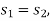let dryness fraction at 2 be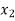

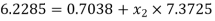
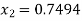
Hence enthalpy at state 2,

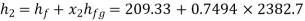
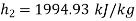
Steam turbine work

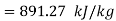
Turbine output

Q20) Bring 100 kg of steam at 100 kPa, 0.5 dry, to a pressure of 1000 kPa inside a closed vessel. Calculate the mass of dry saturated steam admitted at 2000 kPa for pressure increase. Determine the final quality as well.

A20)

It is a constant volume process,

Volume of vessel V=(Mass of vapour )×(Specific volume of vapour)

Initial specific volume,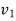

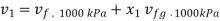
At 100 kPa from steam table;

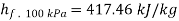
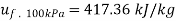
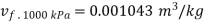
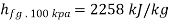
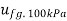=2088.7 kJ/kg

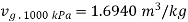
Given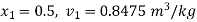

Enthalpy at 1,

Internal energy in the beginning=

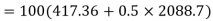
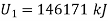
Let the mass of dry steam added be ‘m’, final specific volum inside vessel,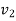

At 2000 kPa, from steam table

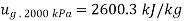
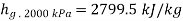
Total mass inside vessel=Mass of steam at 2000kPa + Mass of mixture at 100kPa

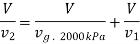
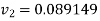
Substituting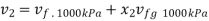

At 1000 kPa from steam table

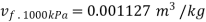
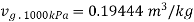
It gives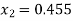

For adiabatic mixing

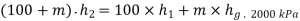
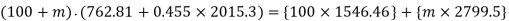
It gives upon solving

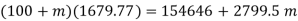
Mass of dry steam at 2000 kPa to be added=11.91 kg

Quality of final mixture=0.455