UNIT 1
Two-dimensional force systems and Friction
Q.1 Explain newton's first law of motion?
Sol: Newton’s first law states that, if a body is at rest or moving at a constant speed in a straight line, it will remain at rest or keep moving in a straight line at constant speed unless it is acted upon by a force. This postulate is known as the law of inertia. The law of inertia was first formulated by Galileo Galilei for horizontal motion on Earth and was later generalized by René Descartes. Before Galileo, it had been thought that all horizontal motion required a direct cause, but Galileo deduced from his experiments that a body in motion would remain in motion unless a force (such as friction) caused it to come to rest.
Q.2 Principle of Transmissibility of forces
Sol: The state of the rigid body will not change if the force acting on a body is replaced by another force of the same magnitude & direction acting anywhere on the body along the line of action of the replaced force. The value of force will not change along the Line of action of force within the body.
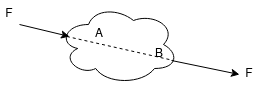
Q.3 Explain the method of resultant force?
Sol: Methods for the resultant force
Though there are many methods for finding out the resultant force of a number of given forces, yet the following are important from the subject point of view:
2. Method of resolution.
The analytical method includes the Parallelogram law of Vectors which is described as “If two forces, acting simultaneously on a particle, be shown by two sides of a parallelogram, then the resultant will be the diagonal between these sides of a parallelogram.”
Mathematically, resultant force,
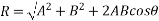
Where R is the resultant force, A and B are component vectors and 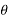 is the angle between the two vectors, as shown below.
is the angle between the two vectors, as shown below.
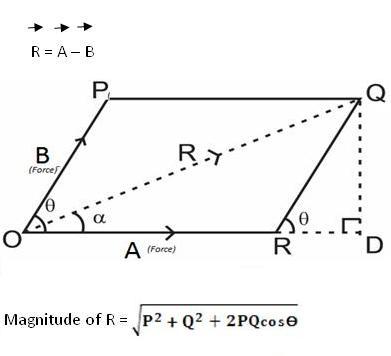
For finding the direction of resultant vector, we need to find the angle between A and R i.e. 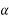 .
.

Q.4 What is a free body diagram?
Sol: Free body diagrams
If a body is shown with all external forces acting on it so that the body is in equilibrium, such a diagram is called a free body diagram. To draw the free body diagram, we have to remove all the restrictions like wall, floor, hinge, any other support and replace them by reactions which these support extents on the body.
Ex – 1) Draw FBD of a bar supported and loaded as shown below.
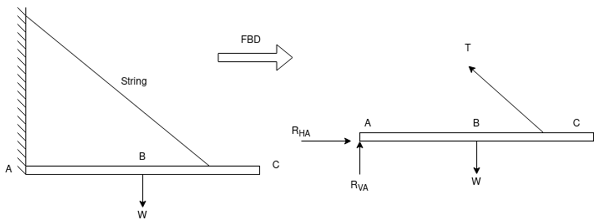
2) Draw FBD of sphere supported as shown below
Q.5 Explain kinetic friction?
Sol: Kinetic Friction FR is the resisting force that acts on a body after the Force of static friction has been overcome. Coulomb experimentally determined the following properties of kinetic friction:
Kinetic friction is proportional to the normal force FN:
FR = μk N F
It shows no considerable dependence on the contact area or roughness of the
Surface.
The coefficient of kinetic friction is approximately equal to the coefficient of
Static friction:
μk s ≈ μ
Q.6 Explain Static Friction?
Sol: In order to set in motion a body lying on an even surface in a
State of rest, a critical force, the force of static friction Fs, must be overcome. This
Force is roughly proportional to the normal force FN 1:
Fs = μs N F.
The coefficient μs is called the coefficient of static friction. It is dependent on the
The pairing of the contacting materials, however, shows almost no dependence on the contact area or roughness.
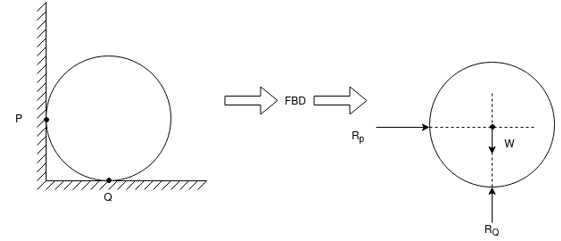
Q.7 Explain Friction in Flat Belts?
Sol:
For a flat belt, the belt or cable will interact with the bottom surface. For a V belt, the belt or cable will interact with the sides of a groove.
A flat belt is any system where the pulley or surface only interacts with the bottom surface of the belt or cable. If the belt or cable instead fits into a groove, then it is considered a V belt.
When analyzing systems with belts, we are usually interested in the range of values for the tension forces where the belt will not slip relative to the surface. Starting with the smaller tension force on one side (T1) we can increase the second tension force (T2) to some maximum value before slipping. For a flat belt, the maximum value for T2 will depend on the value of T1, the static coefficient of friction between the belt and the surface, and the contact angle between the belt and the surface (Beta) given in radians, as described in the equation below.
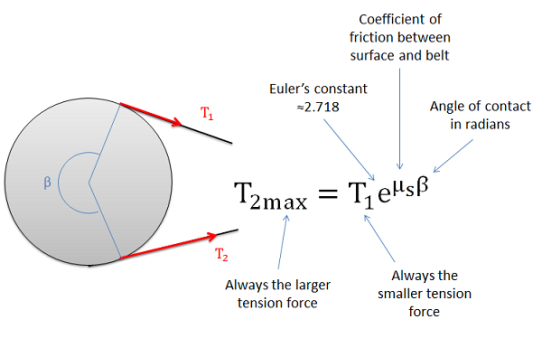
The maximum value of T2 before the belt starts slipping can be determined with the equation above.
Q.8 Explain newton's second law?
Sol: Newton’s second law is a quantitative description of the changes that a force can produce on the motion of a body. It states that the time rate of change of the momentum of a body is equal in both magnitude and direction to the force imposed on it. The momentum of a body is equal to the product of its mass and its velocity. Momentum, like velocity, is a vector quantity, having both magnitude and direction. A force applied to a body can change the magnitude of the momentum, or its direction, or both. Newton’s second law is one of the most important in all of physics. For a body whose mass m is constant, it can be written in the form F = ma, where F (force) and a (acceleration) are both vector quantities. If a body has a net force acting on it, it is accelerated in accordance with the equation. Conversely, if a body is not accelerated, there is no net force acting on it.
Q.9 Explain Friction in V Belts?
Sol: A V belt is any belt that fits into a groove on a pulley or surface. For the V belt to be effective, the belt or cable will need to be in contact with the sides of the groove, but not the base of the groove as shown in the diagram below. With the normal forces on each side, the vertical components must add up the same as what the flat belt would have, but the added horizontal components of the normal forces, which cancel each other out, increase the potential for friction forces.
The equation for the maximum difference in tensions in V belt systems is similar to the equation in flat belt systems, except we use an "enhanced" coefficient of friction that takes into account the increased normal and friction forces possible because of the groove.

In a V belt, the "enhanced" coefficient of friction takes into account the coefficient of friction between the two materials as well as the groove angle.
As we can see from the equation above, steeper sides to the groove (which would result in a smaller angle alpha) result in an increased potential difference in the tension forces. The trade-off with steeper sides however is that the belt becomes wedged in the groove and will require force to unwedge itself from the groove as it leaves the pulley. This will cause losses that decrease the efficiency of the belt-driven system. If very high tension differences are required, chain-driven systems offer an alternative that is usually more efficient.
Q.10 Explain newton's third law?
Sol: Newton’s third law states that when two bodies interact, they apply forces to one another that are equal in magnitude and opposite in direction. The third law is also known as the law of action and reaction. This law is important in analyzing problems of static equilibrium, where all forces are balanced, but it also applies to bodies in uniform or accelerated motion. The forces it describes are real ones, not mere bookkeeping devices. For example, a book resting on a table applies a downward force equal to its weight on the table. According to the third law, the table applies an equal and opposite force to the book. This force occurs because the weight of the book causes the table to deform slightly so that it pushes back on the book like a coiled spring.