UNIT 2
Beam and Trusses
Q.1 Find the support reactions of a given beam for loading as shown below.
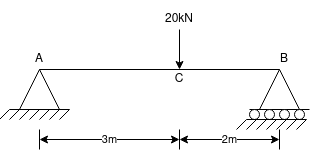
Sol  Draw FBD of a given beam & applying conditions of equilibrium
Draw FBD of a given beam & applying conditions of equilibrium
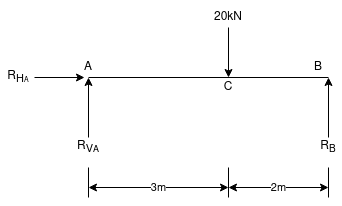
∑fx = 0
RHA = 0
∑fxy = 0
RVA – 20 + RB = 0
RVA + RB = 20 ----(1)
Taking moments at A
∑MA = 0
(20 × 3) – (RB × 5) = 0
60 – 5RB
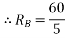
RB = 12 kN  put in equation (1)
put in equation (1)
 RVA + 12 = 20
RVA + 12 = 20
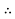 RVA = 20-12
RVA = 20-12
RVA = 8 kN 
Q.2 Find support reaction for a given beam
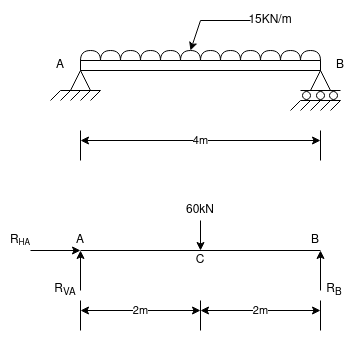
Sol:
 Resolving forces horizontally
Resolving forces horizontally
∑fx = 0
RHA = 0
Resolving forces vertically
∑fy = 0
RVA – 60 + RB = 0
RVA + RB = 60 -------(1)
Taking moment at A
∑MA = 0
(60 × 2) – (RB × 4 ) = 0
 120 – 4RB = 0
120 – 4RB = 0
 RB =
RB = 
RB = 30 kN 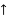
Q.3 Find the support reactions of a given loading for Beam.
Sol:
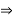 Resolving forces horizontally
Resolving forces horizontally
∑fX = 0
RHA = 0
Resolving forces vertically
∑fY = 0
RVA – 60 + RB = 0
RVA + RB = 60 ----------------- (1)
Taking moments at A
∑ MA = 0
(RVA × 0) + (60 × 2.67) – 4RB = 0
160.2 – 4RB = 0
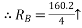 Put in equation (1)
Put in equation (1)
We get
RVA + 40 = 60
RVA = 60 – 40
RVA = 20 kN 
Q.4 Find the support reactions for a given beam.

Sol:
 Resolving force horizontally
Resolving force horizontally
∑fX = 0
RHA = 0
Resolving forces vertically
∑fy = 0
RVA + RB = 0 --------------(1)
Taking moments at A
 40 – 7RB = 0
40 – 7RB = 0
 RB =
RB = 
RB = 5.71 kN 
Put the above value in equation (1)
RVA + RB = 0
RVA + 5.71 = 0
RVA = - 5.71 kN
RVA = 5.71 kN 

Resolving forces horizontally
∑fX = 0
RHA = 0
Resolving forces vertically
∑fy = 0
RVA – 240 + RB = 0
RVA + RB = 240 -------------(1)
Taking moment at A
∑ MA = 0
(240 × 3) – 80 – 6RB = 0
640 – 6RB = 0
RB = 106.67 kN 
Put this value in equation (1)
RVA + RB = 240
RVA = 240 – 106.67
RVA = 133.33 kN 
Q.5 Find support reactions for the loading as shown below:

Sol:
 Resolving forces vertically
Resolving forces vertically
∑fy = 0
RVA – 50 – 20 – 120 + RB = 0
RVA + RB = 190 -------------(1)
Resolving forces horizontally
∑fX = 0
RHA = 0
Taking moments at A
∑ MA = 0
(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0
100 + 80 + 720 – 8RB = 0
900 – 8RB = 0
RB – 112.5 kN 
Put above value in equation (1)
RVA + 112.50 = 190
RVA = 77.5 kN 
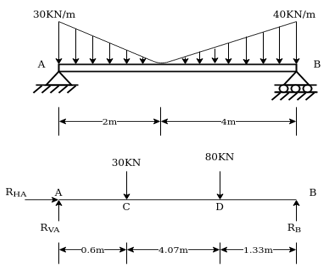
Q.6 Find the reactions at support A & B.
Sol:
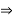 Resolving forces vertically
Resolving forces vertically
∑fy = 0
RVA – 30 – 80 + RB = 0
RVA + RB = 110 ---------(1)
Resolving forces horizontally
∑fX = 0
RHA = 0
Taking moments at A
∑ MA = 0
(30 × 0.6) + [80 × (4.07 + 0.6)]- (6 × RB) = 0
18 + 373.6 – 6RB = 0
6RB = 391.6
RB= 65.267 kN
Put above value in equation (1)
RVA + RB = 110
RVA + 65.267 = 110
RVA = 110 – 65.267
RVA = 44.733 kN
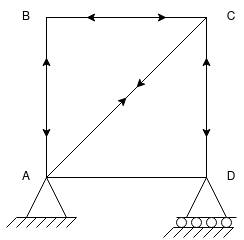
Q.7 Determine the forces in all members of the truss by a joint method
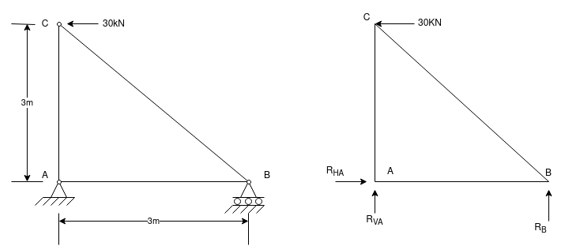
Sol:
Consider FAB of Truss, Applying conditions of equilibrium,
 = 0
= 0
RHA + 30 Kn
 = 0
= 0
RvA + RB =0
Taking moment at point A, = 0
= 0
-(RB* 3) - (30*3) = 0
RB = -30 KN
RB =30 KN RVA = 30 KN
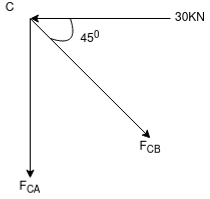
Consider Joint c, Assuming forces in member AC & BC to be
Tensile, Applying conditions of equilibrium,
 = 0
= 0
-30 + FCB cos 45 =0
FCB =30/cos 45 = 42.42 KN (T)
-  = 0
= 0
- FcA – FCB sin 45=o
- F cA -42.42 sin 45 =0
-FCA – 30= 0
-FCA = -30 KN
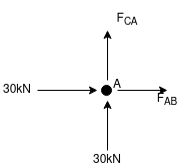
Consider Joint c, Assuming forces in member AC & BC to be
Tensile, Applying conditions of equilibrium,
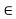 Fx = 0 30+FAB =0
Fx = 0 30+FAB =0
FAB = -30KN
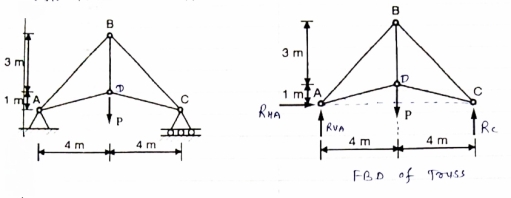
Q.8 Determine the forces in each member of the plane truss as shown in fig. in terms pf the external loading and state if the members are in tension or compression. Use 0+ 30 deg, L = 2 m and p =100N.
Diagram
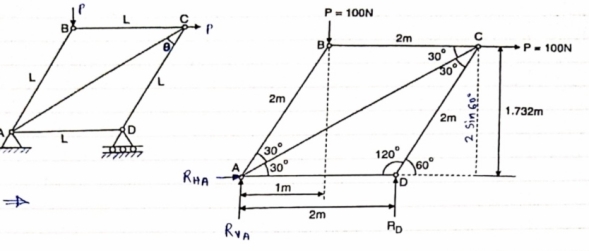
Sol: Consider FBD of Truss,
For equilibrium,  Fx =0
Fx =0
RHA+100 =0
RHA =-100 KN
 Fy =0 RVA = RD – 100 ….. 1
Fy =0 RVA = RD – 100 ….. 1
MA = 0 -------Taking moment @ A
- (Roxz) + (100*1) + (100*1.732) =0
- - 2 Rd + 100 + 1.7320 =0
- -2 Rd + 100 + 173.2 =0
- RD =136.66 N ()
From eqn (1)
RVA = 100 – 136.6
RVA= 36.6N
RVA = 36.6 N
Consider Joint D, for equilibrium,
Fx =0
-FAD + FCD cos 60 =0 – (11)
Fy = 0
136.6 +FCD sin 60 +0
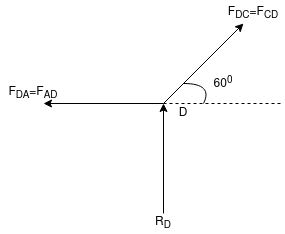
FCD = -157.73 N ©
From eqn (11), Fad =- 78. 87 N (c)
Consider point A, for the equilibrium of point A,
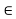 Fx = 0
Fx = 0
- 100 + FAD + FAc cos + 30 FAb cos60 = 0
-100 + (-78.87) +FAC cos 30 +FAb cos60 =0
FAc cos 30 + FAB cos60 + 178. 87 (3)
 fx =0
fx =0
-36.6 + FAC sin 30 + FAB sin 60 =0
FAC sin 30 + FAb sin 60 = 36.6
Solving eqn (3) and (4)
FAC = 273.21 N (T)
FAB = -115.47 N
FAB= 115.47 N ©
Consider point B, for the equilibrium of point,
 Fx =0
Fx =0
-FAB cos60 + FBC =0
-[9-115.47) cos60]+ FBC =0

FBC = -57.73 N
FBC =57.73N
Member | AB | BC | CD | AD | AC |
force | 115.47N | 57.73N | 157.73N | 78.87N | 273.21N |
Nature | c | c | c | c | T |
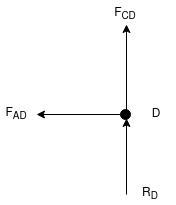
Q.9 Determine the axial forces in each member of the plane truss as shown in the figure.
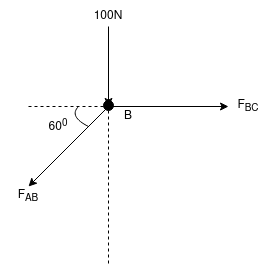
Sol: Consider FBD of Truss,
For the equilibrium of Truss,  fx =0
fx =0
RHA + 10 =0
RHA = -10 KN
RHA =10KN (
Resolving forces vertically,
 fy =o
fy =o
RVA + RD -15 =0
RVA + RD = 15 …… (1)
Taking moment about point A,
 Fy =0
Fy =0
(10*3) – 3 Rd =0
30+ 3 Rd =0
RD= 10 KN 
RVA = 5KN ( )
)
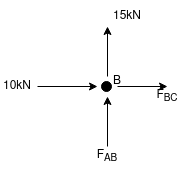
Now Consider joint B, FBD of joint B is shown below.
Assumbing forces developed in all members to be Termile,
For the equilibrium of joint We have
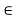 fx =0
fx =0

10+FBC =0
FBC = -10 KN
FBC = 10KN (c)
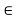 fy =0
fy =0
FAB = -15 KN
FAB = 15 KN (c)
Now consider joint c,
For the equilibrium of joint,
 fx =0
fx =0
-FBC – FAC cos 45 =0
- (-10) – FAC cos 45=0
10= FAC cos 45
FAC = 10/cos 45
FAc = 14.14 KN (T)
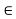 fy =0
fy =0
-Fac sin 45 – FCD=0
- 14.14 sin45 = FCD
FCD = -10 KN (c)
FCD= 10 KN (c)
Consider joint D,
By observation,
FAD=0

Sr .No | Member | Force | Nature |
1 | AB | 15 KN | c |
2 | BC | 10KN | c |
3 | CD | 10KN | c |
4 | DA | 0 | - |
5 | AC | 14.14 | T |
Q.10 Member AB & BC can support a maximum compressive force of 800 N & members AD, DC, BD can support max. Tensile. Force of 2000N Determine the greatest land p that
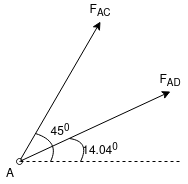
Sol: Consider the following geometry of the figure.
tan 1 = ¼
1 = ¼
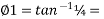 14.04
14.04
 2 =
2 = 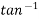 =45
=45
Consider
 fx =0 RHA = 0
fx =0 RHA = 0
∈Fy =o RVA + Rc = p……(1)
∈ma =0
Hp- 8 Rc =0
Rc =P/2 N ( ) RvA = (P/2) N (
) RvA = (P/2) N ( )
)
Consider point A C assuming all forces as Tensile)
∈fx =0
FAD cos 14.04+FAB cos 45 =0… (2)
∈fy = 0 p/2= Fad sin 14.04 + FAB sin 45 =0….. (3)
FAB = 2743.9 N > 800 N (Not Allowed)
Let FAD = 2000 N (T) Then from equation (2) & (3)
FAB =-274.9 N > 800 (Not allowed)
Let FAB = .800 N ©, Then put this equation (2) (3) we get
FAB = 583 N < 2000 N (Allowed) From Equation (2) P= 848.9 N