UNIT 5
Simple stress and strain, Pure bending of beams and Torsion
Q.1 Explain Longitudinal Strain?
Sol:
There are two types of strain :
A longitudinal strain is defined as Change in the length to the original length of an object It is caused due to longitudinal stress and is denoted by the Greek letter epsilon 𝜺.
Longitudinal Strain Formula
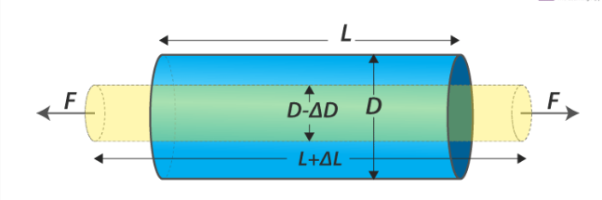
Consider a cylinder. When that longitudinal stress acts on it, there will be a change in the length of the cylinder. Then the longitudinal strain can be mathematically expressed as follows:
Longitudinal Strain=Change in the length / Original Length ε=ΔL/L |
Where,
Longitudinal Strain Unit
It is expressed as ε=Δ L / L. Here the fundamental unit of length is the meter. Substituting it in the formula we get:
SI Unit of Longitudinal Stress = mm
They cancel each other, making it unit less or dimensionless quantity.
Longitudinal Strain Meaning
Stress and strain are like two sides of a coin. It is important to know their behaviour at microscopic scales. We know that all solids are elastic by nature. Atoms or molecules constitute them. Each atom or molecule is surrounded by neighbouring atoms or molecules. Each atom or molecule surrounded by neighbouring atoms or molecules is bonded together by intermolecular forces and stay in equilibrium. When a deforming force or external force is applied, their intermolecular or inter-atomic distances vary. As a result, a restoring force will be generated to attain back the equilibrium, thereby regaining the original size and shape.
When an object is subjected to deforming force, the restoring force will be generated to oppose the deforming force and get back the original shape and size. The restoring force has a magnitude same as that of applied force but in the opposite direction. This restoring force per unit area is called stress.
Consider a cylinder (figure above) with L as length and D as the diameter. What happens to the cylinder when an equal force is applied such that it is perpendicular to the cross-sectional area? The answer is there will be a change in its length as well as in diameter. The length will increase from L to L+ΔL and Diameter will reduce from D to D-ΔD. Thus, the change in dimension to the original dimension is defined as strain. It tells the amount of stress an object is experiencing.
When the object is stretched, the restoring force is known as tensile stress. When the object is compressed, the restoring force is known as compressive stress. In both cases, there will be a considerable change in the length of the object, say, a cylinder. Thus we can define “longitudinal strain as Change in the Length ΔL to Original Length L”.
Q.2 Explain the Bulk Modulus Of Elasticity
Sol: Today we will look at the interesting topics in physics that are bulk modulus. To begin with, the bulk modulus is defined as the proportion of volumetric stress related to the volumetric strain of specified material, while the material deformation is within the elastic limit. To put in more simple words, the bulk modulus is nothing but a numerical constant that is used to measure and describe the elastic properties of a solid or fluid when pressure is applied on all the surfaces.
The bulk modulus of elasticity is one of the measures of the mechanical properties of solids. Other elastic modules include Young’s modulus and Shear modulus. In any case, the bulk elastic properties of a material are used to determine how much it will compress under a given amount of external pressure. Here it is important to find and note the ratio of the change in pressure to the fractional volume compression.
The value is denoted with a symbol of K and it has the dimension of force per unit area. It is expressed in the units per square inch (psi) in the English system and newtons per square meter (N/m2) in the metric system.
Following is the table explaining other related concepts:
Bulk Modulus Of Elasticity Formula
It is given by the ratio of pressure applied to the corresponding relative decrease in the volume of the material.
Mathematically, it is represented as follows:
B = ΔP /(ΔV/V)
Where:
B: Bulk modulus
ΔP: change of the pressure or force applied per unit area on the material
ΔV: change of the volume of the material due to the compression
V: Initial volume of the material in the units of in the English system and N/m2 in the metric system.
Q.3 What is the bulk modulus of a body that experienced a change of pressure of 5*104N/m2 and its volume goes from 4 cm3 to 3.9 cm3?
Sol:
The bulk modulus is calculated using the formula,
B = ΔP /(ΔV/V)
B = (5*104 N/m2)/((4 cm3 – 3.9 cm3)/4 cm3) = 0.125 *104 N/m2
B = 1.25 *104 N/m2
Q.4 Explain the uses of bulk modulus
Sol: Uses
Bulk modulus is used to measure how incompressible a solid is. Besides, the more the value of K for a material, the higher is its nature to be incompressible. For example, the value of K for steel is 1.6×1011 N/m2 and the value of K for glass is 4×1010N/m2. Here, K for steel is more than three times the value of K for glass. This implies that glass is more compressible than steel.
Now, a quick exercise for you. Try finding the value for diamond and comparing it with the value of steel and glass.
Consider this situation. You go deep-sea diving into the Mariana Trenches. This is the following information you have in hand.
Bulk Modulus of Bone = 1.5×1010 N/m2
Atmospheric Pressure = 1.01×105 N/m2
The pressure at deep point = 1.09×108 N/m2
You have two tasks;
While in solids, Young’s modulus is commonly used, the value of K varies in gases, as they are extremely compressible. The concept of Bulk Modulus is also used in liquids. Temperatures of fluid and entrained air content are the two factors highly controlled by the bulk modulus.
Q.5 Explain Tensile Stress
Sol: When the material is under tension, it is known as tensile. The forces that are acting along the axis of force are responsible for the stretching of the material. The external force per unit area of the material resulting in the stretch of the material is known as tensile stress.
Tensile stress is a quantity associated with stretching or tensile forces. It is responsible for the elongation of the material along the axis of the applied load. Tensile stress is defined as:
The magnitude F of the force applied along an elastic rod divided by the cross-sectional area A of the rod in a direction that is perpendicular to the applied force.
Ductile materials have the tendency to withstand the load while brittle materials fail before reaching the ultimate material strength.
When a tensile force acts on the material, the following tensile properties can be calculated:
Tensile Stress Formula
σ=F/A |
Where,
Q.6 Explain Shearing Stress
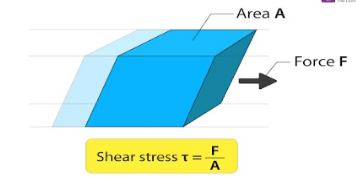
Sol: The process of parallel layers sliding past each other is known as shearing. A pile of papers, a pack of cards with rectangular cross-sections can be pushed to obtain a parallelogram cross-section. In such cases, the angle between the sides has changed, but all that has actually happened is some parallel sliding. In this article, let us discuss shearing stress in detail.
When an external force acts on an object, It undergoes deformation. If the direction of the force is parallel to the plane of the object. The deformation will be along that plane. The stress experienced by the object here is shear stress or tangential stress.
It arises when the force vector components are parallel to the cross-sectional area of the material. In the case of normal/longitudinal stress, The force vectors will be perpendicular to the cross-sectional area on which it acts.
Shearing Stress is defined as:
“A type of stress that acts coplanar with a cross-section of material.”
Shear stress arises due to shear forces. They are the pair of forces acting on opposite sides of a body with the same magnitude and opposite direction. Shear stress is a vector quantity. This means, here the direction is also involved along with magnitude. It is denoted by the Greek alphabet: τ. The SI unit of shear stress is N/m2 or Pa
How is Shearing Stress Calculated?
Average shear stress can be calculated by taking the ratio of force per unit area
τ=FA |
Where,
Q.7 Discuss Shearing Stress in Fluids
Sol: Shear stress is observed in fluids too. When a fluid flows within the boundary of solids, the shear stress is observed along with the point of contact between fluid and boundary. Fluid comprises of various levels, each level travel at different speeds. The layers which are at the same height from the boundary experience the same speed. This varying speed between the layers is also a result of shear stress. In fluids, stress and strain are related differently. Here, shear stress is proportional to strain rate with viscosity as proportionality constant.
Shearing Strain in Real Life
The moment you wake up and crawl on the bed to get out of the bed, till you go back to sleep. Almost every instance of the day to day activity involve shear stress. Some of such real-life scenarios are listed below-
Q.8 Relation between Elastic Constants
Sol: Young’s modulus, bulk modulus, and Rigidity modulus of an elastic solid are together called Elastic constants. When a deforming force is acting on a solid. It results in a change in its original dimension. In such cases, we can use the relation between elastic constants to understand the magnitude of deformation.
Elastic constant formula
E=9KG/ G+3K |
Where,
Individually Young’s modulus and bulk modulus and modulus of rigidity are related as-
| Formula | SI Units |
The relation between modulus of elasticity and modulus of rigidity | E=2G(1+μ) | N/m2 or pascal(Pa) |
The relation between Young’s modulus and bulk modulus | E=3K(1−2μ) | N/m2 or pascal(Pa) |
Derivation of the relation between elastic constants
We can derive the elastic constant’s relation by combining the mathematical expressions relating terms individually.
Young modulus can be expressed using Bulk modulus and Poisson’s ratio as –
E=3K(1−2μ)
Similarly, Young’s modulus can also be expressed using rigidity modulus and Poisson’s ratio as-E=2G(1+2μ)
Combining the above two-equation and solving them to eliminate Poisson’s ratio we can get a relation between Young’s modulus and bulk modulus k and modulus of rigidity as -E=9KG / G+3K
Hope you understood the relation between Young’s modulus and bulk modulus k and modulus of rigidity.
Q.9 When a force of 1000 N is applied on a body, it gets compressed by 1.2 mm. Determine the strain energy.
Sol:
Given:
Force F = 1000 N,
Compression δ = 1.2 mm
Strain energy formula is given by,
U = Fδ / 2
= 1000 ×1.2×10−3 / 2
Therefore, U = 0.6 J.
Q.10 A rod of area 90 mm2 has a length of 3 m. Determine the strain energy if the stress of 300 MPa is applied when stretched. Young’s modulus is given as 200 GPa.
Sol:
Given:
Area A = 90 mm2
Length l = 3m
Stress σ = 300 MPa
Young’s modulus E = 200 GPa
Volume V is given by the formula
V = area*length
= (90 × 10−6) × 3
V = 270 x 10−6 m3
The strain energy formula is given as,
U = σ2 / 2E× V
= (300×106)2 / 2 x 200×109 x 270 x 10-6
Therefore, U = 83.3 x 106 J
Therefore, the strain energy of the rod is 83.3 x 106 J
Q.11 A rod of area 90 square mm has a length of 3 m. Then find out the strain energy if the stress of 300 MPa is applied when stretched. Young’s modulus is 200 GPa.
Sol: Given parameters are,
Area A = 90 square mm,
Length, l = 3m,
Stress, σ=300MPa=300×106Paσ=300MPa=300×106Pa
Young’s modulus, E=200GPa.=200×109PaE=200GPa.=200×109Pa
Volume V is: V = AL
=(90×10−6)×3=(90×10−6)×3
V=27×10−6cubicmV=27×10−6cubicm
The strain energy formula is:
U=σ22E×V.U=σ22E×V.
=300×10622×200×109×27×10−6.=300×10622×200×109×27×10−6.
= 12.15 J
Therefore, the strain energy of the rod will be 12.15 J.