Unit 1

Partial differential equation

Question-1: Form a partial differential equation from-

Sol.

Here we have-

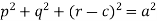
It contains two arbitrary constants a and c

Differentiate the equation with respect to p, we get-

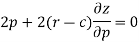
Or

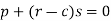
Now differentiate the equation with respect to q, we get-

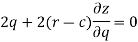
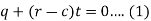
Now eliminate ‘c’,

We get

Now put z-c in (1), we get-

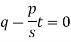
Or

Question-2: Solve the differential equation-

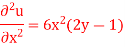
Sol: Given the boundary condition that-

At x = 0,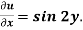

Sol.

Here we have-

On integrating partially with respect to x, we get-

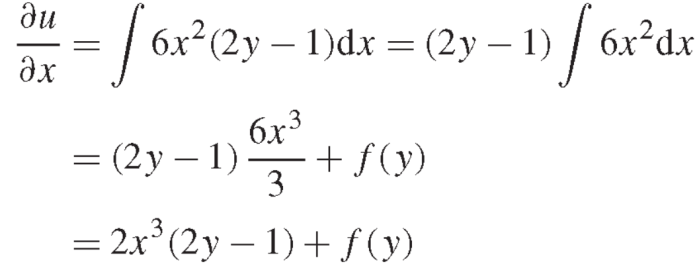
Here f(y) is an arbitrary constant.

Now form the boundary condition-

When x = 0,

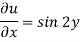
Hence-

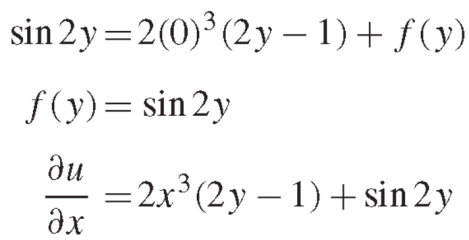
On integrating partially w.r.t.x, we get-

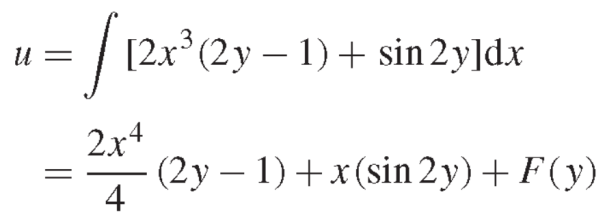
Question-3: Solve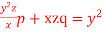

Solution. Rewriting the given equation as

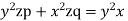
The subsidiary equations are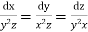

The first two fractions give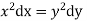

Integrating we get 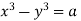   n    (i)

Again the first and third fraction give xdx = zdz

Integrating, we get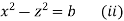

Hence from (i) and (ii), the complete solution is

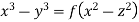
Question-4: Solve-

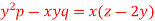
Sol.

We have-

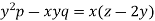
Then the auxiliary equations are-

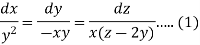
Consider the first two equations only-

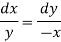
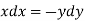
On integrating

…….. (2)

Now consider the last two equations-

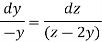
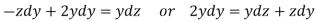
On integrating we get-

…………… (3)

From equation (2) and (3)-

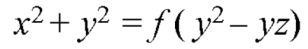
Question-5: Solve-

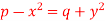
Sol.

Let-

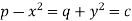
That means-

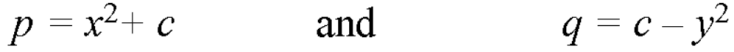
Put these values of p and q in

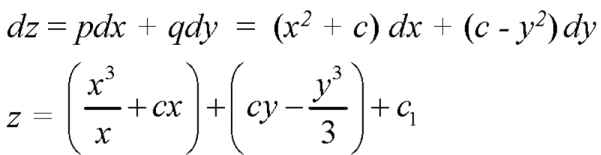
Question-6: Solve-

Sol.

Let
 

Charpit’s subsidiary equations are-

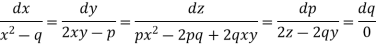
So that- dq = 0 or q = a

 On putting q = a in (1) we get-

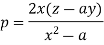
Such that-

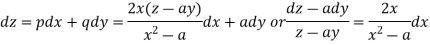
Integrating

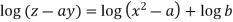
Or

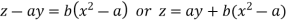
Which is the required solution.

Question-7: Find the characteristics of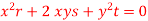

Sol.

Here we have-

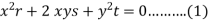
Now comparing (1) with-

Rr + Ss + Tt + f(x, y, z, p, q) = 0

We get-

R =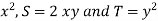

Now we see that-

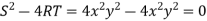
Hence the equation is parabolic.

The 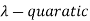is given by-

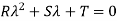
Putting the values of R, S, and T in this, we get-

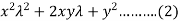
Now simplifying (2), we get-

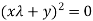
Solving it we get the repeated roots given by

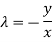
Therefore we get only ne family of the characteristic of (1).

The characteristic equation of (1) is-

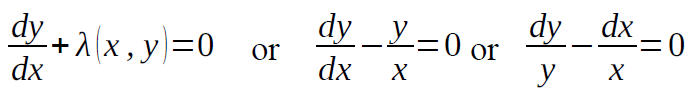
On integrating, we get-

log y – log x = log

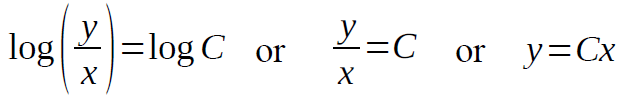
Which is the required family of characteristics and it represents a family of straight lines passing through the origin.

Question-8: Solve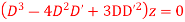

Solution.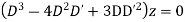

Its auxiliary equation is

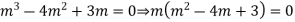
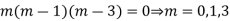
The required solution is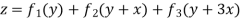

Question-9: Solve

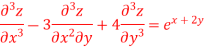
Solution.

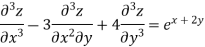
Given equation in symbolic form is

(D3-3D2 D'+4D'3)z=ex+2y

It’s A.E. is 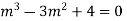where m = -1,2, 2

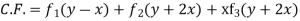
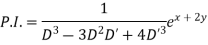
Put, D=1,D’=2 

Hence the complete solution is

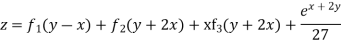
Question-10: Solve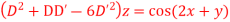

Sol.

A.E. is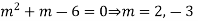

C.F. =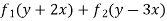

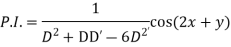
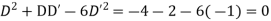
It is a case of failure.

Now,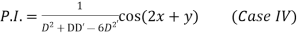

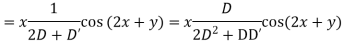
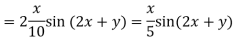
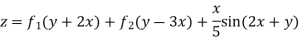
Question-11: Solve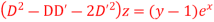

Solution.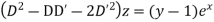

A.E. is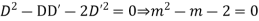

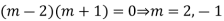
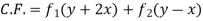
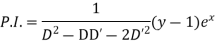
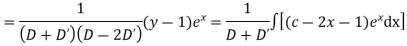
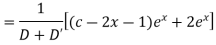
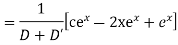
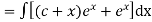
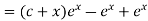
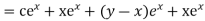
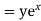
 Hence the complete solution is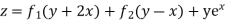

Question-12: Solve

Solution.

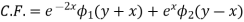
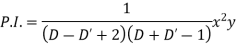
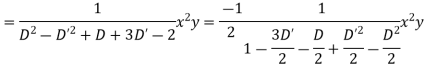
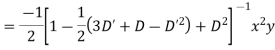
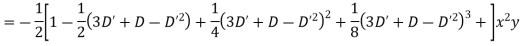
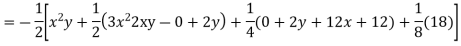
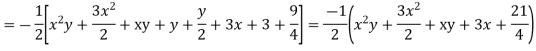
Hence the complete solution is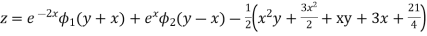

Question-13: Solve-

Sol.

The above PDE can be written as-

Now put

Which gives-

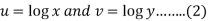
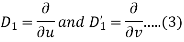
Then the equation (1) can be written as-

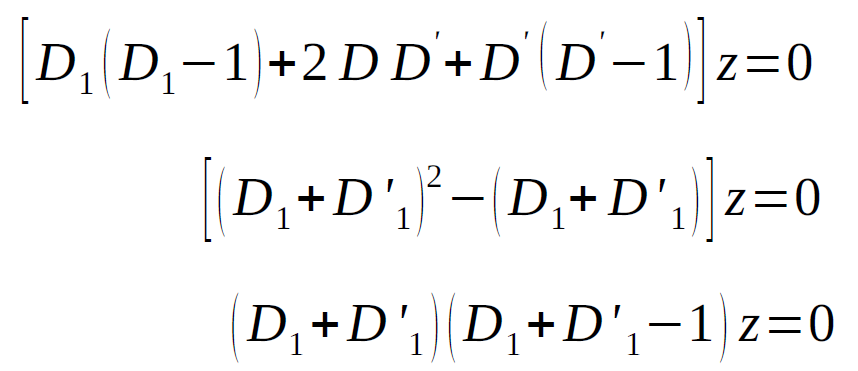
Hence the required solution will be-