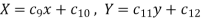Unit 2
Applications of partial differential equation
Question-1: Classify the following PDEs into hyperbolic, parabolic, or elliptic.

Solution.
In the first PDE, a = 1, b = 0 and c = 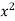
So that-
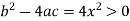
Thus we can say that the given PDE is hyperbolic.
Now in the second PDE,
A = 1, b = 0 and c = 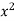
So that-
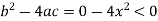
Therefore the second PDE is elliptic.
Question-2: Using the method of separation of variables, solve
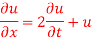
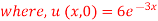
Solution. 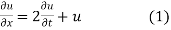
Let, u = X(x). T (t). (2)
Where X is a function of x only and T is a function of t only.
Putting the value of u in (1), we get
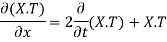
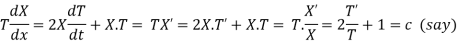
(a) 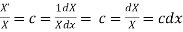
On integration log X = cx + log a = log 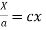
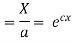
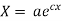
(b)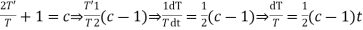
On integration 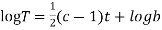
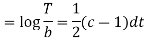
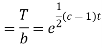
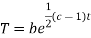
Putting the value of X and T in (2) we have
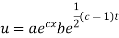
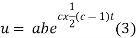
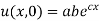
But, 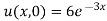
i.e. 
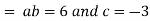
Putting the value of a b and c in (3) we have

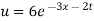
Which is the required solution.
Question-3: Using the method of separation of variables, solve 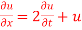 Where
Where 
Solution.
Assume the given solution 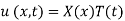
Substituting in the given equation, we have

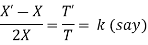
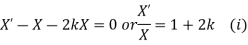
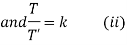
Solving (i) 
From (ii) 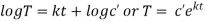
Thus 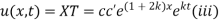
Now, 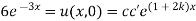
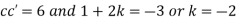
Substituting these values in (iii) we get
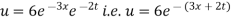
Which is the required solution
Question-4: Find the deflection of a vibrating string of unit length having fixed ends with initial velocity zero and initial deflection f (x)=k (sinx –sin2x)
Solution.
By d’Alembert’s method, the solution is
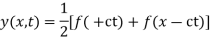
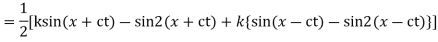

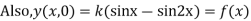
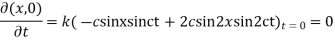
i.e., the given boundary corrections are satisfied.
Question-5: Find the deflection u(x,y,t) of the square membrane with a = b = 1 and c = 1. If the initial velocity is zero and the initial deflection is f(x, y) =  .
.
Solution.
Here taking a = b = 1 and f(x, y) =  in equation above (5)-
in equation above (5)-
We get-
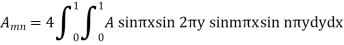
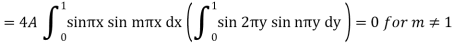

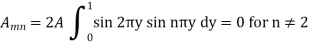
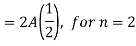

Also from equation (3) above-
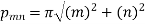
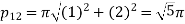
Therefore from equation (4),
The solution will be-

Question-6: A rod of length 1 with insulated sides is initially at a uniform temperature u. Its ends are suddenly cooled to 0° Celsius and are kept at that temperature. Prove that the temperature function u (x, t) is given by
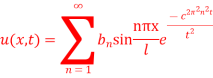
Where 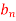 is determined from the equation.
is determined from the equation.

Solution.
Let the equation for the conduction of heat be
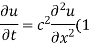
Let us assume that u = XT, where X is a function of x alone and T that of t alone.
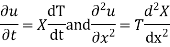
Substituting these values in (1) we get 
i.e. 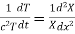
Let each side be equal to a constant 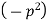
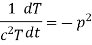

And 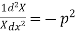
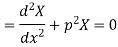
Solving (3) and (4) we have
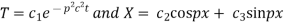
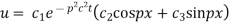
Putting x = 0, u = 0 in (5), we get

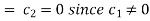
(5) becomes 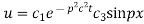
Again putting x = l, u =0 in (6), we get
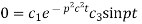

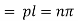
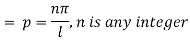
Hence (6) becomes 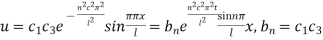
This equation satisfies the given conditions for all integral values n. Hence taking n = 1, 2, 3,…, the most general solution is
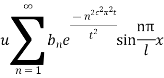
By initial conditions 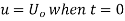
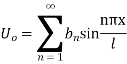
Question-7: The ends A and B of a rod 20 cm long having the temperature at 30 degree Celsius and at 80 degree Celsius until steady-state prevails. The temperature of the ends is changed to 40 degrees Celsius and 60 degrees Celsius respectively. Find the temperature distribution in the rod at time t.
Solution.
The initial temperature distribution in the rod is
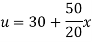
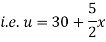
And the final distribution (i.e. steady-state) is
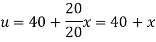
To get u in the intermediate period, reckoning time from the instant when the end temperature was changed we assumed
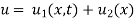
Where 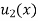 is the steady-state temperature distribution in the rod (i.e. temperature after a sufficiently long time) and
is the steady-state temperature distribution in the rod (i.e. temperature after a sufficiently long time) and 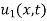 is the transient temperature distribution which tends to zero as t increases.
is the transient temperature distribution which tends to zero as t increases.
Thus, 
Now 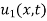 satisfies the one-dimensional heat flow equation
satisfies the one-dimensional heat flow equation
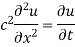
Hence u is of the form

Since 

Hence 
Using the initial condition i.e.
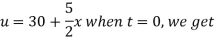
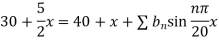
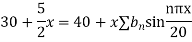
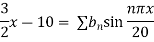

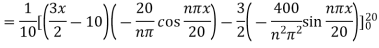
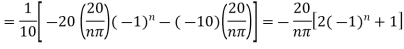
Putting this value of 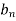 n (1), we get
n (1), we get
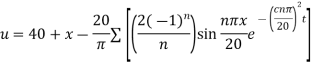
Question-8: Solve Laplace’s equation  subject to the conditions u(0, y) = u(l, y) = u(x, 0) = 0 and u(x, a) = sin n
subject to the conditions u(0, y) = u(l, y) = u(x, 0) = 0 and u(x, a) = sin n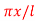
Solution. The three possible solutions of Laplace’s equation-
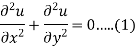
are-
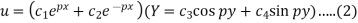
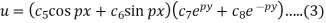
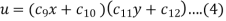
We need to solve equation (1) satisfying the following boundary conditions-
u(0, y) ........... (5)
u(l, y) = 0........(6)
u(x, 0) = 0 ..........(7)
and u(x, a) = sin n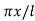 ...... (8)
...... (8)
using (5), (6) and (2), we get-
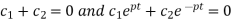
Solving these equations, we get-
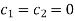
Which leads to a trivial solution.
Similarly, we get a trivial solution by using (5), (6), and (4).
Hence the solution for the present problem is the solution (3).
Now using (5) in (3), we get-
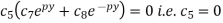
Therefore, equation (3) becomes-
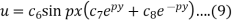
Using (6), we get-
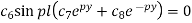
Therefore either-
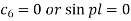
If we take 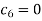 then we get a trivial solution.
then we get a trivial solution.
Thus sin pl = 0 whence 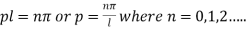
Equation (9) becomes-
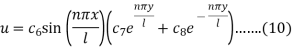
Using (6), we have 0 = 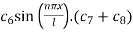
i.e.
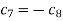
Thus the solution suitable for this problem is-
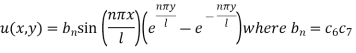
Now using the condition (8)-
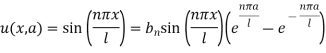
We get-
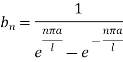
Hence the required solution is-
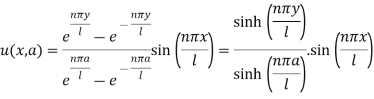
Question-9: A transmission line 1000 km long is initially under steady-state conditions with potential 1300 volts at the sending end (x = 0) and 1200 volts at the receiving end (x =1000). The terminal end of the line is suddenly grounded but the potential at the source is kept at 1300 volts.
Assuming the inductance and leakage to be negligible, find the potential v(x, t ).
Solution.
We know that the equation of the telegraph line is-
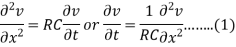
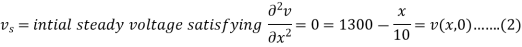
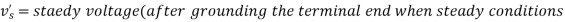

So that-
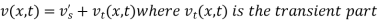
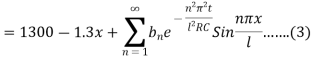
Where l = 1000 km
Putting t = 0, we get from (2) and (3)
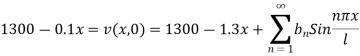
I.e.
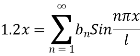
Where-
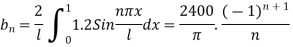
Hence
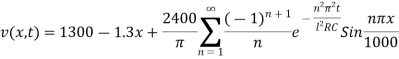
Question-10: Define Laplace’s equation in two dimensions and its solution.
Solution.
The equation-
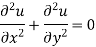
Is known as Laplace’s equation in two dimensions.
The solution of Laplace’s equation-
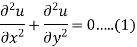
Let
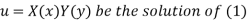
Put the value in (1), we get-
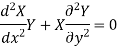
Separating the variables-
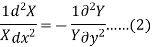
Since x and y are the independent variables, equation (2) can hold good only if each side of (2) is equal to a constant (k),
Then (2) leads the ordinary differential equation-
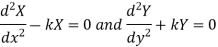
On solving these equations, we get-
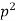
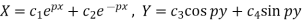
2. When k is negative and it equals to 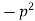 , say
, say
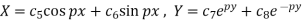
3. When k is zero-