Unit - 4

Thin cylinders & spheres and Thick cylinders

Q1) Derive the expression for circumferential stress or Hoop stress developed in the wall of cylindrical shell.

A1) 

Let us consider here following terms:
P = Internal fluid pressure

d = Internal diameter of thin cylindrical shell

t = Thickness of the wall of the cylinder
L = Length of the cylindrical shell

σH = Circumferential stress or hoop stress developed in the wall of the cylindrical shell.
Cylindrical shell bursting will take place if force due to internal fluid pressure will be more than the resisting force due to circumferential stress or hoop stress developed in the wall of the cylindrical shell.

In order to secure the expression for circumferential stress or hoop stress developed in the wall of the cylindrical shell, we will have to consider the limiting case i.e. force due to internal fluid pressure should be equal to the resisting force due to circumferential stress or hoop stress.

Force due to internal fluid pressure = Internal fluid pressure x Area on which fluid pressure will be acting

Force due to internal fluid pressure = P x (d x L)

Resisting force due to circumferential stress = σH x 2 L t

As we have seen above, we can write following equation as mentioned here.

Force due to internal fluid pressure = Resisting force due to circumferential stress

P x d x L = σH x 2 L t

σH = P x d / (2 t)

σH= P x d/ 2t

Longitudinal (Axial) Stress

For a cylinder closed in both ends the internal pressure creates a force along the axis of the cylinder. The longitudinal stress caused by this force can be calculated as

σL = p d / (4 t)                              

Where,

σl = longitudinal stress (MPa, psi)

P = Internal fluid pressure

d = Internal diameter of thin cylindrical shell

t = Thickness of the wall of the cylinder

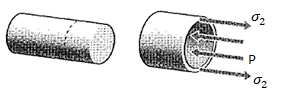
The stresses σz in the axial direction of a cylindrical pressure vessel with closed ends are found using this same approach as seen in Fig. 3, and yielding the same A)

P (πr2) = σz(2πr) t

σz=pr/2t

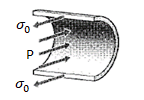
However, a different view is needed to obtain the circumferential or “hoop” stresses σθ. Considering an axial section of unit length, the force balance gives 2σθ (t x 1) = p* (2r x 1)

σθ=pr/t

Q2) Derive the expression for the condition when a thin cylinder is closed at both ends and subjected to internal pressure.

A2)

Consider a thin cylinder closed at both ends and subjected to internal pressure ‘p’ as shown in the figure. Let d=Internal diameter, t = Thickness of the wall L = Length of the cylinder.

Consider a small length ‘dl’ of the cylinder and an elementary area ‘dA’ as shown in the figure.

Consider a small length ‘dl’ of the cylinder and an elementary area ‘dA’ as shown in the figure.

Force on the elementary area,

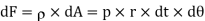
Horizontal component of this force

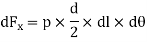
Vertical component of this force

∴ Total diametrical bursting force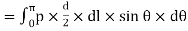

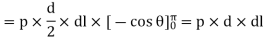
∴ Resisting force (due to circumferential stress 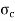)=2

Under equilibrium, Resisting force=Bursting force

i.e., 2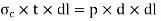

Circumferential stress

Force due to fluid pressure= p × area on which p is acting = 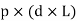(bursting force)

Force due to circumferential stress = is acting

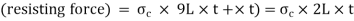
∴ Circumferential stress, 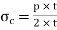  …… (1)

Q3) Derive the expression for the thick cylinder.

A3)

Consider a thick cylinder of external radius r1 and internal radius r2, containing a fluid under pressure ‘p’ as shown in the fig.

Let ‘L’ be the length of the cylinder.

Consider an elemental ring of radius ‘r’ and thickness ‘δr’ as shown in the above figures. Let pr and (pr+ δpr) be the intensities of radial pressures at inner and outer Consider the longitudinal section XX of the ring as shown in the fig. The bursting force is evaluated by considering the projected area,

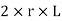for the inner face and for the inner face and for the outer face.

The net bursting force,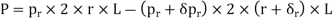

×

Bursting force is resisted by the hoop tensile force developing at the level of the strip

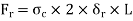
Thus, for equilibrium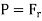

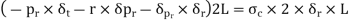
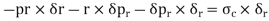
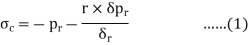
Longitudinal strain is constant. Hence we have

Since 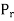is compressive

Since , E and μ are constants should be constant. Let it be equal to 2a. Thus

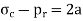
From (1),

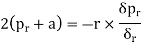
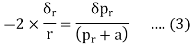
Integrating,

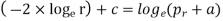
Where c is constant of integration. Let it be taken as , where b is another constant.

Thus,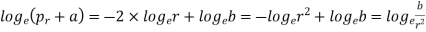

or radial stress,

Substituting it in equation 2, we get

Hoop stress,

The equation (4) and (5) are known as “Lame’s Equations” for radial pressure and hoop stress at any specified point on the cylinder wall.

Thus .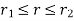

Q4) Derive the expression when sphere subjected to internal pressures.

A4)

Sphere subjected to internal pressures.

Consider a simple spherical vessel of radius r and wall thickness t, such as a round balloon. An internal pressure p induces equal biaxial tangential tensile stresses in the walls, which can be denoted using spherical rθφ coordinates as σθ and σφ.

The magnitude of these stresses can be determined by considering a free body diagram of half the pressure vessel, including its pressurized internal fluid.

The fluid itself is assumed to have negligible weight. The internal pressure generates a force of pA= p (πr2) acting on the fluid, which is balanced by the force obtained by multiplying the wall stress times its area,

σφ(2πrt) Equating these:

P (πr2) = σφ (2πrt)

σφ = pr/2t

Note that this is a statically determined result, with no dependence on the material properties. Further, note that the stresses in any two orthogonal circumferential directions are the same;

I.e., σφ= σθ.

The accuracy of this result depends on the vessel being “thin-walled,” i.e. r>>t. At the surfaces of the vessel wall, a radial stress σr must be present to balance the pressure there. But the inner-surface radial stress is equal to p, while the circumferential stresses are p times the ratio (r/2t). When this ratio is large, the radial stresses can be neglected in comparison with the circumferential stresses.

Q5) A vessel in the shape of the spherical shell of 1.20 m internal diameter and 12 mm shell thickness is subjected to pressure of 1.6 N/mm^2. Determine the stress induces in the material of the vessel.

A5)

Given:

Internal diameter, d=1.2m=1.2×103mm

Shell thickness, t=1.2mm

Fluid pressure, p=1.6 N/mm2

The stress induced in material of spherical shell is given by

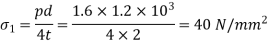
Q6) A spherical vessel 1.5 m diameter is subjected to an internal pressure of 2 N/mm^2. Find the thickness of the plate required if maximum stress is not exceed 150 N/mm^2 and joint efficiency is 75%.

A6)

Given: Diameter of shell,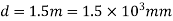

Fluid pressure,

Stress in material,

Joint efficiency,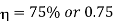

Let

The stress induced is given by,

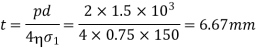
Q7) Find the speed of rotation of a wheel of diameter 750 mm, if the hoop stress is not exceed 120 N/mm^2. The wheel has a thin rim and density of wheel is 7200 Kg/m^3.

A7) 

Given: Diameter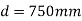

Max. Hoop stress,

Density,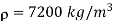

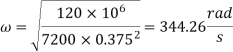
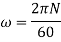
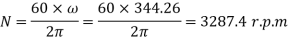
Q8) A thick spherical shell of 20 mm internal diameter is subjected to an internal fluid pressure of 7 N/mm^2. If the permissible tensile stress in the shell /material is 8 N/mm^2, find the thickness of the shell.

A8)

Given: Internal diameter =200 mm

Internal radius

Internal fluid pressure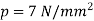

Permissible tensile stress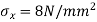

The radial pressure and hoop stress at any radius of spherical shell are given by

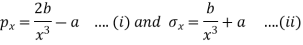
Th hoop stress, 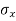will be maximum at the internal radius. Hence permissible tensile stress of 8 N/mm2 is the interval radius.

At x=100 mm,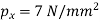

Substituting these values in equation (i), we get

At x=100 mm,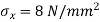

Substituting the values in equation (iii), we get

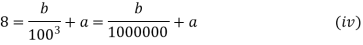
Adding equation (iii) and (iv), we get

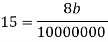
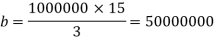
Substituting the value in equation (iv), we get

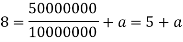
Substituting the values of a and b in equation (i), we get

Let 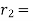External radius of the shell.

At outside, the pressure

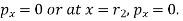
Substituting these values in equation (v), we get

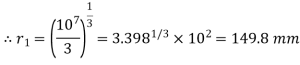
Thickness of the shell,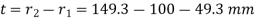

Q9) Determine the maximum and minimum hoop stress across the section of the pipe of 400 mm internal diameter and 10 mm thick, when pipe contain a fluid in the pressure of 8 N/mm^2.

A9)

Given:

Internal diameter = 400 mm

Internal radius,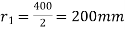

Thickness =100 mm

External diameter = 400+2×100=600 mm

External radius,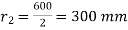

Fluid pressure,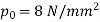

At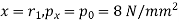

Now apply the boundary conditions to the above equaitons. The booundary conditions

1. At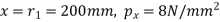

2. At

Substituting these boundary conditions in equation (i), we get

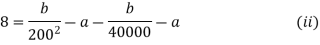
Subtracting equation (iii) from (ii), we get

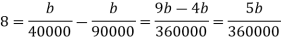
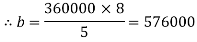
Substituting this value in equation (iii), we get

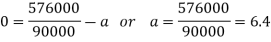
The values of a and b are substituted in the hoop stress.
Now hoop stress at any radius x is given by equation

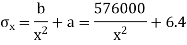
At

At

Q10) Wall thickness of a cylindrical shell of 800-mm internal diameter and 2-m long is I0 mm. If the shell is subjected to an internal pressure of 1.5 MPa, find the following:

• The maximum intensity of shear stress induced
• The change in dimensions of the shell

E = 205 GPa & =0.3

A10)

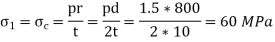
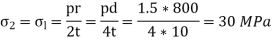
Maximum shear stress at any point in the thickness of metal,

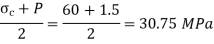
Change in dimension,

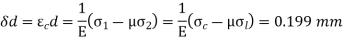
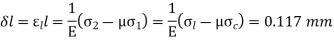
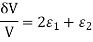
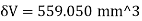
Q11) A cast-iron pipe of 750-mm diameter is used to carry water under a head of 60 m. Determine the thickness of the pipe if the permissible stress is to be 20 MPa.

A11)

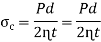
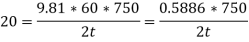
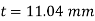
Q12) A boiler of 1.6-m diameter is made of 20-mm thick steel plates. Determine the permissible steam pressure in the boiler if the efficiency of the longitudinal joint of the boiler is 80% and maximum tensile stress in the steel plates is not to exceed 80 MPa. What will be the circumferential stress in the solid plate section at this pressure! Also calculate the longitudinal stress in the plate section through the rivets of the circumferential joint if the efficiency of the joint is 70%.

A12)

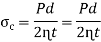
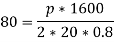
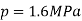
Circumferential stress in the solid plate,

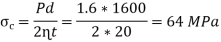
At Circumferential joint,

Q13) A spherical shell of 1.2-m internal diameter and 6-mm thickness is filled with water under pressure until the volume is increased by 400 X I 03 mm3. Find the pressure exerted by water on the shell. Take E= 204 GPa and v = 0.3.

A13)

Internal volume of shell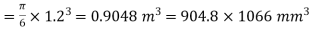

Hoop strain

Volumetric strain =3×hoop strain

Or 

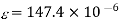
Hoop stress

Neglecting the radial stress,

  or

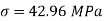
Radial pressure

Q14) Find the thickness of the cylinder of a hydraulic ram of 5O-mm internal diameter to withstand an internal pressure of 30 MPa. The allowable tensile stress is limited to 45 MPa and the allowable.

A14)

Hoop stress constraint

At,

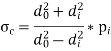
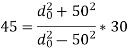
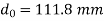
Shear stress constraint

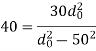
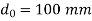
Thickness,

Q15) A thick cylinder of 200-mm outside diameter and 140-mm inside diameter is subjected to internal pressure of 40 MPa and external pressure of 24 MPa. Determine the maximum shear stress in the material of the cylinder at the inside diameter.

A15)

Equations for thick cylinders

When a cylinder is acted upon by internal and pressures, the radial and hoop stresses in terms of constants a and b are

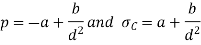
Where the stresses correspond to the diameter d considered.

At inside diameter,

At outside diameter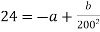

Subtraction (ii) from (i)

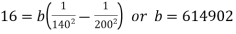
And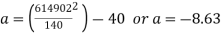

Determination of stresses

Hoop stress at inside diameter

Shear stress,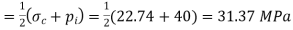

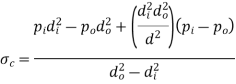
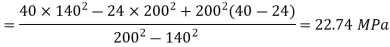
Q16) A compound cylinder is formed by shrinking one tube to another, the inside and outside diameter of the outer tube being 120 mm and 180 mm respectively and of the inner tube being 60 mm and 120 mm respectively. After shrinking, the radial pressure at the common surface is 30 MPa. If the cylinder is subjected to an internal pressure of 80 MPa, determine the final stresses set up at various surfaces of the cylinder. What is the resultant radial pressure at the common surface?

A16)

Shrinkage stresses

Outer tube: pressure is internal;

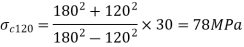
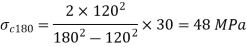
Inner tube: pressure external

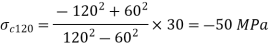
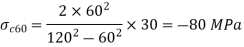
Stresses due to pressure

Cylinder is assumed as a single tube (pressure is internal),

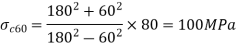
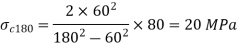
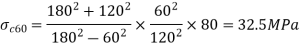
Radial pressure at common surface

Radial pressure at the common surface due to internal pressure

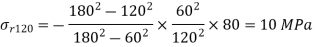
Total radial pressure=30+10=40 MPa

Q17) A bronze bush of 15 mm thickness is shrunk on a steel shaft of 80 mm diameter. If the shrinkage pressure is 60 Mpa, find the tight allowance between bush and the shaft.

	E
Steel	204 GPa	0.28
Bronze	102 GPa	0.32

A17)

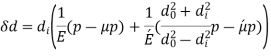
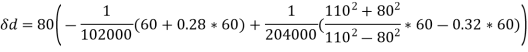
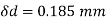
Q18) A solid cylinder with a 400-mm diameter rotates at 2100 rpm. Plot the variation of radial and hoop stresses in the cylinder. What is the maximum hoop stress? Density of the cylinder material is 7700 kg/m3 • Poisson's ratio is 0.3.

A18)

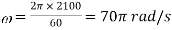
stresses

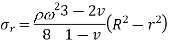
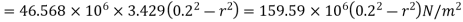
r(m)	0.0	0.04	0.08	0.16	0.18	0.2
	6.38	6.13	5.36	4.09	2.3	0

Hoop stresses

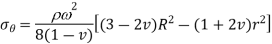
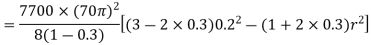
r(m)	0.0	0.04	0.08	0.16	0.18	0.2
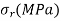	6.38	6.22	5.71	4.85	3.66	2.13

Maximum stress=37.75 MPa

The variation of stresses is shown

Maximum values of hoop and radial stresses =6.38 MPa 

The variation of stresses is shown

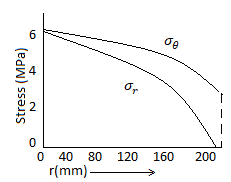
Q19) A hollow cylinder having an outside diameter of 600 mm and an inside diameter of 300 mm rotates at 2400 rpm. Plot the variation of radial and hoop stresses in the cylinder. Density of the cylinder material is 7500 kg/m3. Poisson's ratio is 0.28.

A19)

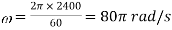
stresses

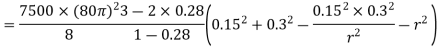
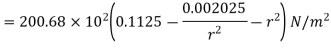
r(m)	0.15	0.18	0.21	0.24	0.27	0.3
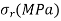	0	3.53	4.51	3.96	2.37	0

Radial stress is maximum at a radius

Its value =4.52 MPa

Hoop stresses

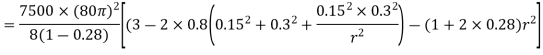
r(m)	0.15	0.18	0.21	0.24	0.27	0.3
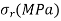	37.75	30.96	26.13	22.24	18.8	15.54

Maximum stress=37.75 MPa

The variation of stresses is shown

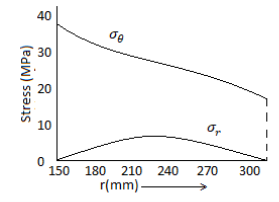
Q20) Differentiate between thin walled and thick-walled pressure vessels.

A20)

The ratio between the mean radius of the vessel and the thickness of the wall determines whether a pressure vessel has thin or thick walls. If this ratio is greater than 10, the vessel is classified as having a thin wall pressure. If the ratio is less than 10, the vessel is classified as having a thick wall pressure.

A thick-walled pressure vessel develops more (circumferential) stress on the inside surface of the vessel, which decreases as the vessel diameter increases.

Radial stress is negligible in thin pressure vessels and is ignored; however, in thick pressure vessels, radial stress is considered alongside longitudinal and transverse stress.

If the thickness of the wall of the cylindrical vessel is less than   of its internal diameter, the cylindrical vessel is known as a thin cylinder. In case of thin cylinders, the stress distribution is assumed uniform over the thickness of the wall.

The ratio of the thickness of the wall to the diameter of the shell determines whether a shell is thin or thick. A shell is considered thin if the ratio is less than about 1 to I 5, otherwise it is thick. In a thin shell, the hoop stresses are assumed to be constant throughout the thickness, and the radial stress is small and can be ignored.