Unit-1
Introduction, Velocity analysis and Acceleration analysis
Q1) Explain types of constrained motion with example.
A1)
1. Completely constrained motion
When the motion between a pair is in a definite direction irrespective of the direction of force applied, then the motion is said to be completely constrained motion.
Example: Motion of the piston in a cylinder (only reciprocating motion)
square bar in a square hole, shaft with collars in a circular hole
2. Incompletely constrained motion
When the motion between a pair or two links can take place in more than one direction, then the motion is called as incompletely constrained motion.
Example: A circular shaft or bar in a circular hole.
3. Successfully constrained motion
When the motion between two elements of a pair is possible in more than one direction but is made to have motion only in one direction by using some external means, it is called as a successfully constrained motion.
Example: A shaft in a foot – step bearing in which shaft may rotate in a bearing or it may move upwards. This the case of incompletely constrained motion, but if the load is placed on the shaft to prevent axial upward movement of the shaft then the motion is said to be successfully constrained motion.
Q2) Differentiate between machine and mechanism.
A2)
Sr. No. | Machine | Mechanism |
1. | Machine may have many mechanisms for transmitting mechanical work or power | When one of the link of a kinematic chain is fixed, then the chain is called a mechanism. |
2. | The basic function of m/c is to obtain mechanical advantage | Mechanism transmits and modifies the motion only. |
3. | Lathe, Milling, Shaper, Heat engine etc. | Geneva, Quick return, slider crank, Four bar mechanism etc. |
A3) Describe Degree of Freedom with example.
A3)
It is defined as the number of independent variables that must be specified to define completely the condition of the system.
Consider an unconstrained rigid body in a space which can describe the following motions.
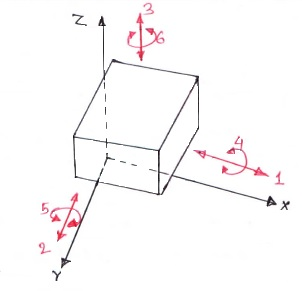
Degree of freedom of a rigid body
Translational Motions along any three-perpendicular axe
Rotational motions about the same axes
 Thus, an unconstrained rigid body in a space have six degrees of freedom.
Thus, an unconstrained rigid body in a space have six degrees of freedom.
Example:
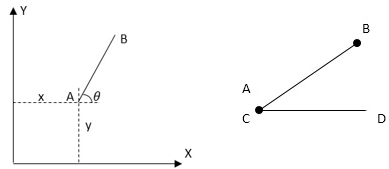
An unconstrained rigid link in the plane has three degrees of freedom (x, y, Q)
(DOF = 3)
If link AB is connected to the link CD by a turning pair at A.
i.e. each pin joint or revolute pair will remove two degrees of freedom.
Only Q is required to specify the motion (DOF = 1)
Q4) Define Kutzbach Criterion for Degree of freedom.
A4) Kutzback criteria has been given by following expression, as mentioned below:-
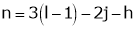
Above equation is called Kutzbach criterion for the mobility of a mechanism having plane motion.
Where,
n = degrees of freedom
l = No. of links
j = No. of binary joints
h = No. of higher pairs
If there is no two degree of freedom pairs (i.e. higher pairs), then h = 0,
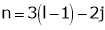
Q5) Calculate degree of freedom of five bar mechanism.
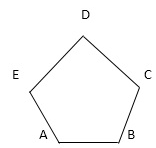
A5) Given, 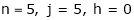
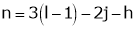
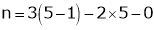
n = 2, where n= degree of freedom
Q6) What is crank lever mechanism? Explain with example.
A6)
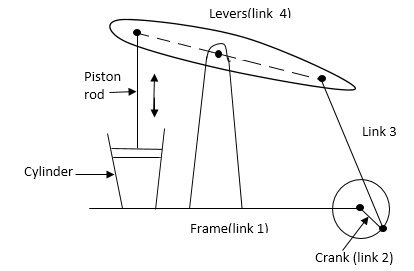
In this mechanism, when the crank rotates about the fixed centre A, the lever oscillates about a fixed centre D. the end E of the lever CDE is connected to a piston rod which reciprocates due to the rotation of the crank:
The purpose of this mechanism is to convert rotary motion into reciprocating motion.
Watt’s Indicator (Double rocker OR double – lever mechanism or oscillating – oscillating converter)
If the link opposite to the shortest link, i.e. link b is fixed and the shortest link ‘d’ is made a coupler, the other two links ‘a’ and ‘c’ could oscillate. The mechanism is known as a rocker – rocker or double – rocker or double – lever mechanism.
The four links are – fixed link at A, link AC, link CE and link BFD. It may be noted that BF and FD from one link because these two parts have no relative motion between them.
The links CE and BFD act as levers. The displacement of the link BFD is directly proportional to the pressure of gas or steam which acts on the indicator plunger.
Q7) What is Instantaneous Centre?
A7) The body can be imagined to rotate about some point on the line perpendicular to the velocity vector passing through that point.
The intersection point of two different lines is called instantaneous centre of rotation (I – centre). An I – centre is a centre of rotation of a moving body relative to another body. It is named as Ipq and it will be in ascending order of the alphabets or digits.

Number of I–centres in a mechanism=N= n( n -1 )/2
Q8) A mechanism has 4 link as 1,2,3 and 4. Calculate the instantaneous centres in the mechanism.
A8) Given n=4 as 1, 2, 3 and 4
We know that the no. of instantaneous centre has formula
N= [n(n-1)]/2=[4(4-1)]/2
N=6, N is no. of instantaneous centre
Q9) Redraw the Mechanism as shown in fig and determine types and number of Pairs, links and degree of freedom.
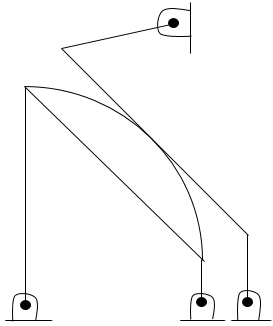
A9) Total no. of links = 7
No. of pairs with 1 degree of freedom = 8
No. of pairs with 2 degree of freedom = 1
From, kutzbach criterion,
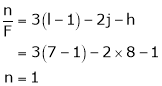
Thus, it is mechanism with one degree of freedom.
Q10) Find degrees of freedom for the mechanism as shown in the following fig.
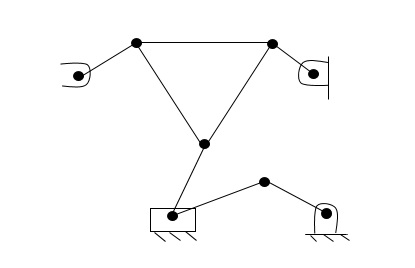
A10)
Total number of links = 8
No. of pairs with 1 degrees of freedom = 10
(At the slider, one sliding pair and two turning pairs)
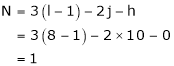
Thus, it is a mechanism with a single degree of freedom.