Unit-4

Balancing and Governors

Q1) Explain Balancing with its type.

A1) It is the process of designing or modifying machinery, so that unbalance is reduced to an acceptable level and if possible is eliminated entirely.

There are basically two types of balancing:-

Static Balancing: A system of rotating masses is said to be in static balance if the combined mass centre of the system lies on the axis of rotation. Net dynamic force acting on the system must be zero.

Dynamic Balancing: A system of rotating masses is in dynamic balance when there does not exist any resultant centrifugal force as well as resultant couple. Net moments about any point in the plane must be zero.

Q2) What is shaking Force?

A2) The resultant of all the forces acting on the body of the engine due to inertia force only is known as shaking or unbalanced force. 

Q3) What it is needed to balance the reciprocating masses?

A3) The major purpose of balancing the reciprocating is to eliminate or remove the shaking forces and a shaking couple evolving in the system.

Q4) What are the effects of partial balancing in locomotive?

A4) Swaying Couple:

The unbalanced forces along the line of stroke for the two cylinders            constitute a couple about the centre line between the cylinders.

The couple trends to sway the engine alternatively in clockwise and

anticlockwise directions. Hence, the couple is known as swaying couple.

Hammer Blow:

The maximum magnitude of the unbalanced force along the perpendicular to the line of stroke is known as hammer blow.

Q5) Define Variations in Tractive force.

A5) Variation in Tractive force:

The resultant unbalanced force due to the two cylinders along the line of stroke is known as tractive force.

Consider the crank of first cylinder be inclined at an angle θ with the line of stroke. The second cylinder has the crank at right angle to the first crank so the angle of inclination for the second crank becomes (90+θ).

Question 6: Given, two cylinder locomotives with cranks at 90 degree. Reciprocating mass per cylinder=300 kg, crank radius 0.3m, driving wheel diameter=1.8 m, distance between cylinder centre line=0.65m, distance between the driving wheel central planes=1.55m. Find: The fraction of the reciprocating masses to be balanced, if the hammer blow is not to exceed 46kN at 96.5kn/h The variation in tractive effort.

A6) Given, m=300 kg, r=0.3 m, D=1.8m or R=0.9m, a= 0.65m,

Mass of reciprocating parts to be balanced= Cm=300C kg3

cylinder wheel

The position of the planes of the wheels and cylinder is shown as fig. 4.10.1(a) and the position of cranks is shown in fig. 4.10.1 (b) assuming the plane of wheel A as the reference plane.

Now the couple polygon, to some suitable scale, may be drawn with the data given in the table (column 6) [fig. 4.10.2]

The closing side of the polygon (vector co) represents the balancing couple and is proportional to 1.55 Bb.

From the couple polygon .

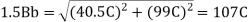
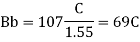
Angular speed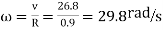  

Hammer blow,

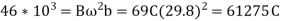
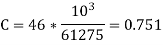
We know that variation in tractive effort

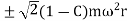
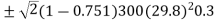
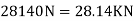
We know that maximum swaying couple

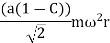
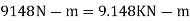
Q7) A single cylinder reciprocating engine has a reciprocating mass of 60 kg. The crank rotates at 60 rpm and the stroke is 320 mm. The mass of the revolving parts at 160 rpm is 50 kg. I the two –thirds of the reciprocating parts and whole of the revolving parts are to be balanced, determine the balance mass required at a radius of 340 mm.

A7)  We know that, Bb= (m1+Cm)r

m1=50 kg , C=2/3, b=340mm, m=60 kg, L=320mm =0.32 m, N=160 rpm

B*0.34=[50+(2/3*60)]*0.16

B*0.34=14.4, B=42.35 kg

Q8) Define Governor with its major types.

A8) It is a device which automatically controls the supply of working fluid to the engine with the varying load conditions and keeps the mean speed within certain limits.

Types of governor: There are basically two types of governor-

1. Centrifugal Governors

2. Inertia Governors.

Q9) Define Centrifugal Governor with example.

A9) It is known as centrifugal governor because it is based on the balancing of centrifugal force on the rotating balls by equal and opposite force that is controlling force.

It works on centrifugal effects produced by rotating balls. As a speed of balls increases, the balls tend to rotate at a greater radius from the spindle axis.

This results into movement of sleeve to upward direction and this movement is attached to the throttle through a bell crank lever and it closes the throttle valve to required extent.

When speed of ball decreases, the balls tend to rotate at a smaller radius and valve is opened according to requirement.

Types of Centrifugal Governor are:

1. Watt Governor

2. Porter Governor

Q10) The length of the upper and the lower arms of the governor are 200 mm and 250 mm respectively. Both the arms are pivoted on the axis of rotation. The central load is 150N, the weight of the each ball is 20 N and the friction of the sleeve together with the resistance of the operating gear is equivalent to a force of 30N at the sleeve. If the limiting inclinations of the upper arms to the vertical are 300 and 400 taking friction into account. Find the range of the speed of governor.

A10) Given, Length of the upper arm=200mm=0.2m, f=30N, θ1=300, θ2=400

Height of governor,

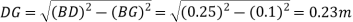
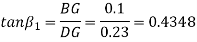
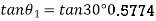
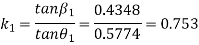
For downward motion of sleeve, the frictional force will act in upward direction. Hence the minimum speed of governor will be,

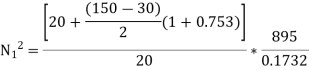
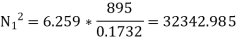
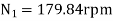
From fig. 4.19.1(b) , the maximum radius of rotation

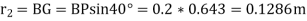
Height of governor,

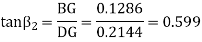
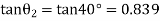
For upward motion of sleeve, the frictional force will act in downward direction, hence the maximum speed of governor will be

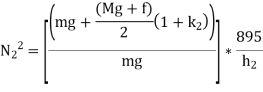
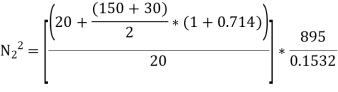
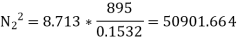
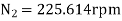
Range of speed =