Unit-5

Brake and Dynamometers and Gyroscope

Q1) What is Friction? Explain it with classification.

A1) When two bodies have relatives motion between each other, a forces acts in the opposite direction of their relative motion, which opposes their motion. This force is called friction force.

Friction force arises due to the relative motion between two bodies and hence some energy is wasted in overcoming the friction.

Classification of friction:

(a)  Static friction: When body is at rest, the friction acts on the on the body is called static friction.

(b)  Dynamic Friction: When body is in motion, the friction acts on the body is called dynamic friction. It is also known as kinetic friction and it is always less than the static friction.

(c)  Dry friction: When two dry and unlubricated surfaces are in contact, the friction acts between them is called dry friction. Sliding friction and rolling friction are examples of dry friction.

(d)  Boundary or greasy friction: When the two rubbing surfaces are separated by a very thin layer of lubricant, the friction is known as boundary friction.

(e)  Film friction: When the two surfaces is in contact are completely separated by a lubricant, friction will occur due to shearing of different layers of the lubricant. This is known as film friction or viscous friction.

Q2) Define Laws of Friction

A2)

F/N= constant

2.     Laws of Kinetic friction: The friction force always acts in the direction opposite to that in which the body is moving. The magnitude of the kinetic friction bears a constant ratio to the normal reaction between the two surfaces. But the ratio is slightly less than that in case of limiting friction. For moderate speeds, the force of friction remains constant but it decreases with increase in speed.

3.     Laws of solid friction: The force of friction is directly proportional to the normal load between the surfaces. The friction force does not depend upon the area of contact surface. Friction depends upon the material of which the contact surfaces are made. Friction does not depend upon the sliding velocity of one body relative to the other.

4.     Laws of fluid friction: The friction force is almost independent of the load. With increase of the temperature of the lubricant, the friction force reduces. Friction does not depend upon the substance of the materials. Friction differs from one lubricant to other.

Q3) Define lubrication and its type.

A3) Lubrication is the admittance of lubricating oil between two surfaces having relative motion in order to reduce friction between them and to ensure smooth running.

There are basically four types of Lubrication, mentioned below:

(a)  Hydrodynamic Lubrication: It is type of lubrication where wedge shaped oil film is built up between the moving block and the surface. In other words moving block acts as a pump to force oil into clearance that narrows down progressively as the block moves.

(b)  Elastohydrodynamic Lubrication: When the load acting on the bearing is very high, the material itself deform elastically against the pressure built up of the oil film. This kind of lubrication is called as elastohydrodynamic lubrication. It happens usually between cam and followers, gear and teeth.

(c)  Boundary Lubrication: If the film thickness between the two surfaces in relative motion becomes so thin that the formation of hydrodynamic oil film is not possible and the surface high spot penetrates this thin to make metal to metal contact then such lubrication is known as boundary lubrication. Such situation can occur due to high load, too thin oil and insufficient supply of oil due to low speed of movement.

(d)  Hydrostatic Lubrication: In this lubrication, a thin oil film resists its instantaneous squeezing out under reversal of loads with relative slow motions.

Q4) Define brake and its classification.

A4) A Brake is device by means of which artificial frictional resistance is applied to a moving machine member, in order retard or stop the motion of a machine. In the process of performing this function, the brake absorbs either kinetic energy of the moving member or potential energy given up by objects being lowered by hoists, elevators etc. The energy absorbed by brakes is dissipated in the form of heat.

Classification of brake:

Q5) The arrangement of an internal expanding friction brake, in which the brake shoe is pivoted at ‘C’ is shown in fig. The distance “CO” is 75mm, O being the centre of the drum. The internal radius of the brake drum is 100mm. The friction lining extends over and arc AB, such that the angle AOC is 135 and angle BOC is 45 . The brake is applied by means of a force at Q, perpendicular to the line CQ, the distance CQ being 150mm.

The local rate of wear on the lining may be taken as proportional to the normal pressure on an element at an angle of with OC and may be taken as equal to 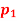sin , where 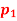is the maximum intensity of normal pressure. The co-efficient of friction may be taken as 0.4 and the braking torque required is 21 N-m. Calculate the force Q required to operate the brake when

A5) Given: OC=75mm;r=100mm ;

;

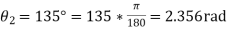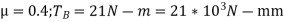
Taking moments about the fulcrum C, we have

Q=56590 / 150=377N Ans. 

Q6) What is Dynamometer?

A6) It is a brake incorporating device to measure the frictional resistance applied. This is used to determine the power developed by the machine, while maintaining its speed at the rated value.

Q7) What is Epi-cyclic train Dynamometer?

A7) An epi-cyclic train dynamometer consists of a simple epi-cyclic train of gears, i.e. a spur gear, an annular gear (a gear having internal teeth) and a pinion. The spur gear is keyed to the engine shaft and rotates in anticlockwise direction. The annular gear is also keyed to the driving shaft and rotates in clockwise direction. The pinion or the intermediate gear meshes with both the spur and annular gears. The pinion revolves freely on a lever which is pivoted to the common axis of the driving and driven shafts.

Q8) Define Torsion Dynamometer.

A8) A torsion dynamometer is used for measuring large powers particularly the power transmitted along the propeller shaft of a turbine or motor vessel.

A little consideration will show that when the power is being transmitted, then the driving end of the shaft twists through a small angle relative to the driven end of the shaft. The amount of twist depends upon many factors such as torque acting on the shaft (J), length of the shaft (l), diameter of the shaft (D) and modulus of rigidity (C) of the material of the shaft.

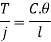
Q9) In a laboratory experiment, the following data were recorded with rope brake. Diameter of the flywheel 1.2 m ; diameter of  the rope 12.5mm; speed of the engine 200 r.pm ; dead load on the brake 600N; spring balance reading 150 N . Calculate the brake power of engine.

A9)  Given: D=1.2 m; d=12.5 m m-0.0125; N= 200 r.p.m; W=600 N ; S=150 N

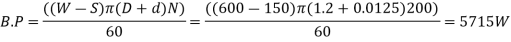
  Ans

Q10) Define Hydraulic Dynamometer.

A10)  Hydraulic accumulator works on the principle of dissipating the power in fluid friction rather than in dry friction. In principle, its construction is similar to that of a fluid flywheel. It consists of inner rotating member or impeller coupled to the shaft of the engine. The impeller rotates in a casing filled with some hydraulic fluid.

Q11) Explain the Angular momentum

A11) We have already discussed that the angular acceleration is the rate of change of angular velocity with respect to time. It is a vector quantity and may be represented by drawing a vector diagram with the help of right hand screw rule (see chapter 2, Art. 2.13)

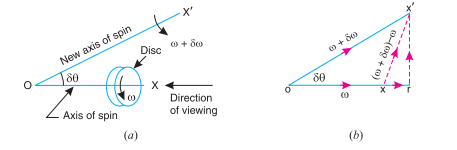
Consider a disc, as shown in Fig. 14.1 (a), revolving or spinning about the axis OX (known as axis of spin) in anticlockwise when seen from the front, with an angular velocity ω in a plane at right angles to the paper. After a short interval of time δt, let the disc be spinning about the new axis of spin OX ′ (at an angle δθ) with an angular velocity (ω + δω). Using the right hand screw rule, initial angular velocity of the disc (ω) is represented by vector ox; and the final angular velocity of the disc (ω + δω) is represented by vector ox′ as shown in Fig. 14.1 (b). The vector xx′ represents the change of angular velocity in time δti.e. the angular acceleration of the disc. This may be resolved into two components, one parallel to ox and the other perpendicular to ox. Component of angular acceleration in the direction of ox

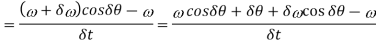
Since δθ is very small, therefore substituting cos δθ=1, we have

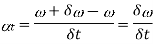
In the limit, when

Component of angular acceleration in the direction perpendicular to

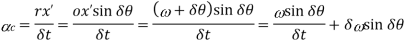
Since δθ in very small, therefore substituting sin δθ=δθ, we have

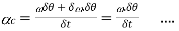(Neglecting 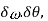being very small)

In the limit, when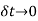

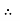Total angular acceleration of the disc

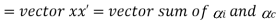
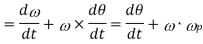
the plane in which the axis of spin is going to rotate. This angular velocity of the axis of spin (i.e. dθ/dt) is known as angular velocity of precession and is denoted by ωP . The axis, about which the axis of spin is to turn, is known as axis of precession. The angular motion of the axis of spin about the axis of precession is known as processional angular motion

Q12) Explain the Gyroscopic couples

A12) Gyroscopic Couple Consider a disc spinning with an angular velocity ω rad/s about the axis of spin OX, in anticlockwise direction when seen from the front, as shown in Fig. 14.2 (a). Since the plane in which the disc is rotating is parallel to the plane YOZ, therefore it is called plane of spinning. The plane XOZ is a horizontal plane and the axis of spin rotates in a plane parallel to the horizontal plane about an axis O Y. In other words, the axis of spin is said to be rotating or processing about an axis O Y. In other words, the axis of spin is said to be rotating or processing about an axis OY (which is perpendicular to both the axes OX and OZ) at an angular velocity ωP rap/s. This horizontal plane XOZ is called plane of precession and O Y is the axis of precession.

 Let I = Mass moment of inertia of the disc about OX, and

ω = Angular velocity of the disc.

∴ Angular momentum of the disc = I.ω

Since the angular momentum is a vector quantity, therefore it may be represented by the vector ox → , as shown in Fig. 14.2 (b). The axis of spin OX is also rotating anticlockwise when seen from the top about the axis O Y. Let the axis OX is turned in the plane XOZ through a small angle δθ radians to the position OX ′, in time δt seconds. Assuming the angular velocity ω to be constant, the angular momentum will now be represented by vector ox′.

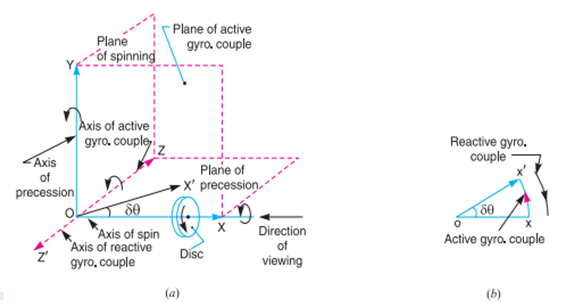
∴ Change in angular momentum

and rate of change of angular momentum

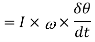
 Since the rate of change of angular momentum will result by the application of a couple to the disc, therefore the couple applied to the disc causing precession,

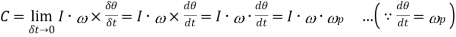
where ωP = Angular velocity of precession of the axis of spin or the speed of rotation of the axis of spin about the axis of precession O Y. In S.I. units, the units of C is N-m when I is in kg-m2.