UNIT 3
Projections and Sections of Solids
QUESTION BANKS
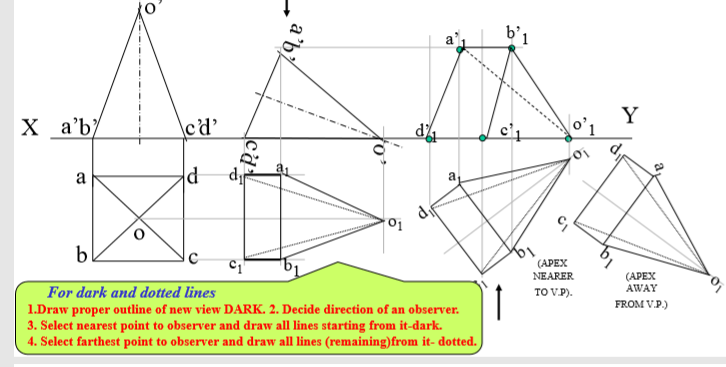
- A square pyramid, 40 mm base sides and axis 60 mm long, has a triangular face on the ground and the vertical plane containing the axis makes an angle of 45 with the VP. Draw its projections. Take apex nearer to VP
Solution Steps :
Triangular face on Hp , means it is lying on Hp:
1.Assume it standing on Hp.
2.It’s Tv will show True Shape of base( square)
3.Draw square of 40mm sides with one side vertical Tv & taking 50 mm axis project Fv. ( a triangle)
4.Name all points as shown in illustration.
5.Draw 2nd Fv in lying position I.e.o’c’d’ face on xy. And project it’s Tv.
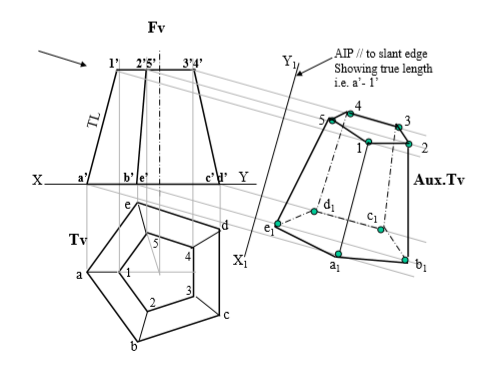
6.Make visible lines dark and hidden dotted, as per the procedure.
7.Then construct remaining inclination with Vp ( Vp containing axis ic the center line of 2nd Tv.Make it 45 to xy as shown take apex near to xy, as it is nearer to Vp) & project final Fv.
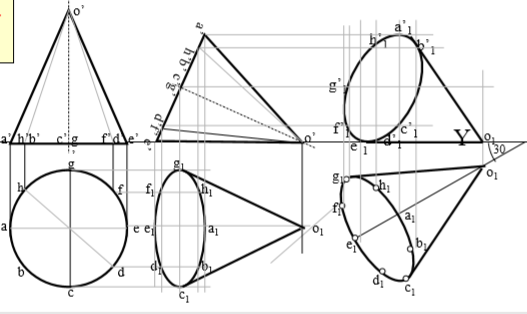
2. A cone 40 mm diameter and 50 mm axis is resting on one generator on Hp which makes 30 inclination with Vp Draw it’s projections.
Solution Steps:
Resting on Hp on one generator, means lying on Hp:
1.Assume it standing on Hp.
2.It’s Tv will show True Shape of base( circle )
3.Draw 40mm dia. Circle as Tv & taking 50 mm axis project Fv. ( a triangle) 4.Name all points as shown in illustration.
5.Draw 2nd Fv in lying position I.e.o’e’ on xy. And project it’s Tv below xy. 6.Make visible lines dark and hidden dotted, as per the procedure.
7.Then construct remaining inclination with Vp ( generator o1e1 30 to xy as shown) & project final Fv
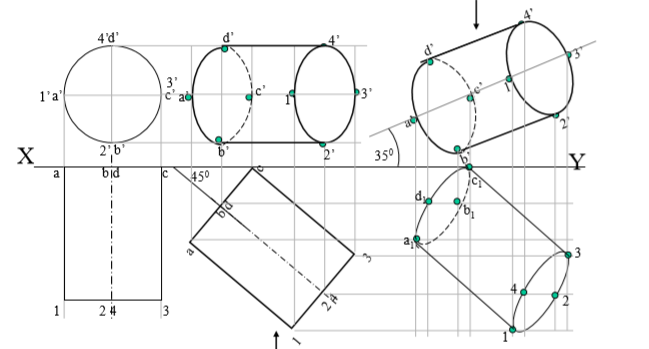
3. A cylinder 40 mm diameter and 50 mm axis is resting on one point of a base circle on Vp while it’s axis makes 45 with Vp and Fv of the axis 35 with Hp. Draw projections..
Solution Steps:
Resting on Vp on one point of base, means inclined to Vp:
1.Assume it standing on Vp
2.It’s Fv will show True Shape of base & top( circle )
3.Draw 40mm dia. Circle as Fv & taking 50 mm axis project Tv. ( a Rectangle) 4.Name all points as shown in illustration.
5.Draw 2nd Tv making axis 450 to xy And project it’s Fv above xy.
6.Make visible lines dark and hidden dotted, as per the procedure.
7.Then construct remaining inclination with Hp ( Fv of axis I.e. center line of view to xy as shown) & project final Tv
4. A square pyramid 30 mm base side and 50 mm long axis is resting on it’s apex on Hp, such that it’s one slant edge is vertical and a triangular face through it is perpendicular to Vp. Draw it’s projections.
Solution Steps :
1.Assume it standing on Hp but as said on apex.( inverted ).
2.It’s Tv will show True Shape of base( square)
3.Draw a corner case square of 30 mm sides as Tv(as shown) Showing all slant edges dotted, as those will not be visible from top.
4.taking 50 mm axis project Fv. ( a triangle)
5.Name all points as shown in illustration. 6.Draw 2nd Fv keeping o’a’ slant edge vertical & project it’s Tv
7.Make visible lines dark and hidden dotted, as per the procedure.
8.Then redrew 2nd Tv as final Tv keeping a1o1d1 triangular face perpendicular to Vp I.e.xy. Then as usual project final Fv.
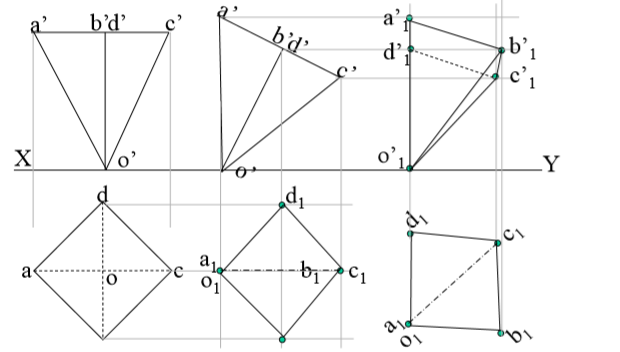
5. A cube of 50 mm long edges is so placed on Hp on one corner that a body diagonal is parallel to Hp and perpendicular to Vp Draw it’s projections.
Solution Steps:
1.Assuming standing on Hp, begin with Tv,a square with all sides equally inclined to xy.Project Fv and name all points of FV & TV.
2.Draw a body-diagonal joining c’ with 3’( This can become // to xy)
3.From 1’ drop a perpendicular on this and name it p’
4.Draw 2nd Fv in which 1’-p’ line is vertical means c’-3’ diagonal must be horizontal. .Now as usual project Tv..
5.In final Tv draw same diagonal is perpendicular to Vp as said in problem. Then as usual project final FV.
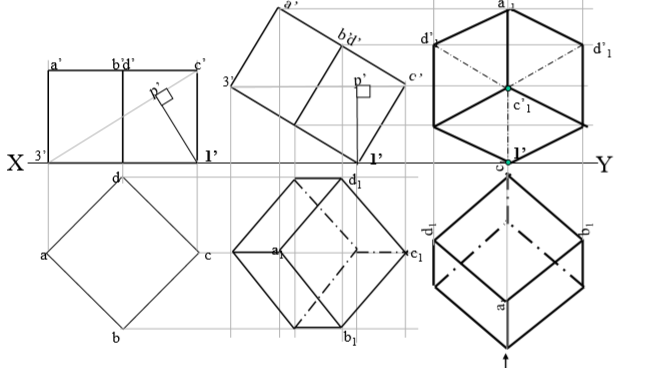
6. A tetrahedron of 50 mm long edges is resting on one edge on Hp while one triangular face containing this edge is vertical and 45 inclined to Vp. Draw projections.
Solution Steps
- As it is resting assume it standing on Hp. Begin with Tv , an equilateral triangle as side case as shown:
- First project base points of Fv on xy, name those & axis line. From a’ with TL of edge, 50 mm, cut on axis line & mark o’ (as axis is not known, o’ is finalized by slant edge length)
- Then complete Fv. In 2nd Fv make face o’b’c’ vertical as said in problem. And like all previous problems solve completely.
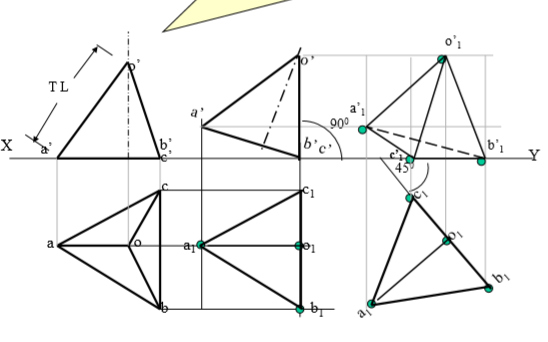
7. A pentagonal pyramid 30 mm base sides & 60 mm long axis, is freely suspended from one corner of base so that a plane containing it’s axis remains parallel to Vp. Draw it’s three views.
Solution Steps:
In all suspended cases axis shows inclination with Hp.
1.Hence assuming it standing on Hp, drew Tv - a regular pentagon, corner case. 2.Project Fv & locate CG position on axis – ( ¼ H from base.) and name g’ and Join it with corner d’
3.As 2nd Fv, redraw first keeping line g’d’ vertical.
4.As usual project corresponding Tv and then Side View looking from
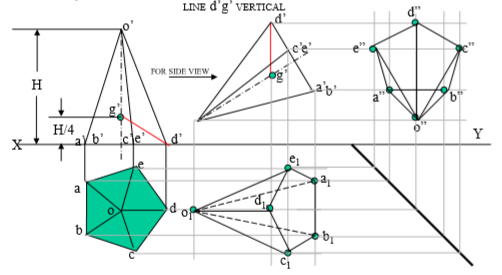
8. A right circular cone, 40 mm base diameter and 60 mm long axis is resting on Hp on one point of base circle such that it’s axis makes 45 inclination with Hp and 40 inclination with Vp. Draw it’s projections.
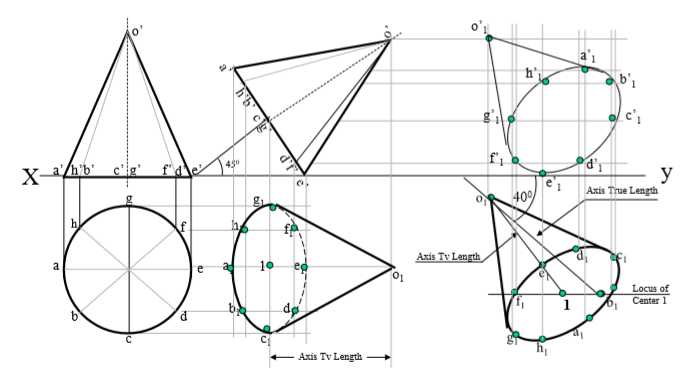
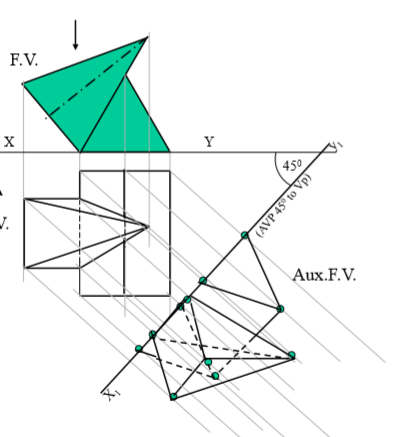
9. A triangular prism, 40 mm base side 60 mm axis is lying on Hp on one rectangular face with axis perpendicular to Vp. One square pyramid is leaning on it’s face centrally with axis // to vp. It’s base side is 30 mm & axis is 60 mm long resting on Hp on one edge of base.Draw FV & TV of both solids.Project another FV on an AVP 450 inclined to VP.
Steps :
Draw Fv of lying prism ( an equilateral Triangle) And Fv of a leaning pyramid. Project Tv of both solids.
Draw x1y1 45 inclined to xy and project aux.Fv on it.
Mark the distances of first FV from first xy for the distances of aux. Fv from x1y1 line.
Note the observer’s directions Shown by arrows and further steps carefully.
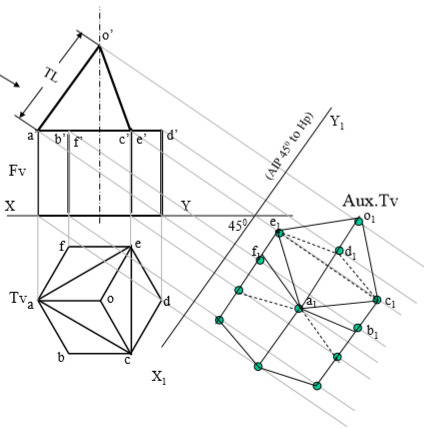
10. A hexagonal prism of base side 30 mm longand axis 40 mm long, is standing on Hp on it’s base with one base edge // to Vp. A tetrahedron is placed centrally on the top of it.The base of tetrahedron is a triangle formed by joining alternate corners of top of prism..Draw projections of both solids. Project an auxiliary Tv on AIP 45 inclined to Hp
STEPS:
Draw a regular hexagon as Tv of standing prism With one side // to xy and name the top points. Project it’s Fv – a rectangle and name it’s top.
Now join it’s alternate corners a-c-e and the triangle formed is base of a tetrahedron as said.
Locate center of this triangle & locate apex o
Extending it’s axis line upward mark apex o’
By cutting TL of edge of tetrahedron equal to a-c. And complete Fv of tetrahedron.
Draw an AIP ( x1y1) 45 inclined to xy And project Aux .Tv on it by using similar Steps like previous problem.
11. A frustum of regular hexagonal pyramid is standing on it’s larger base On Hp with one base side perpendicular to Vp.Draw it’s Fv & Tv. Project it’s Aux.Tv on an AIP parallel to one of the slant edges showing TL. Base side is 50 mm long , top side is 30 mm long and 50 mm is height of frustum.