UNIT 1

Question-1: Find the rank of the following matrix?

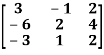
Sol.

Let A =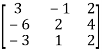

Applying

A 

Applying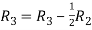

   A 

Applying

A 

Applying

             A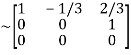 

It is  clear  that  minor  of order 3  vanishes but  minor  of order  2  exists  as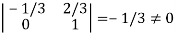 

Hence rank of a given matrix A is 2 denoted by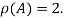 

Question-2: Find the rank of the following matrix?

Sol.

Let  A  = 

Applying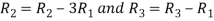

Applying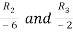

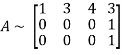
Applying

The minor of   order   3 vanishes but minor of order 2 non zero as 

Hence the rank of matrix A is 2 denoted by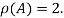

Question-3: Find the rank of the following matrix?

Sol.

Let A =

Apply

Apply

Apply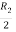

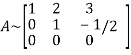
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as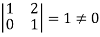 

Hence the rank of given matrix is 2 i.e.

Question-4: Find the rank of the following matrix A-

                                  A =

Sol.  We have,

                              A =

Apply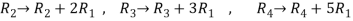

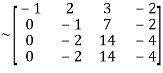
Apply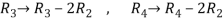 

In this matrix, 4th order and 3rd order minors are zero. But a minor of second order,

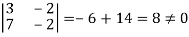
Hence,

                Rank = number of non-zero rows = 2.

Question-5: Find the rank of the following matrix A by triangular form-

                                  A =

Sol. We have,

                                      A =

Apply

                                     A =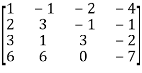

Apply

                                    A =

Apply 

                                  A =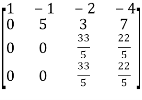

Apply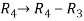 

                                A =

Rank = number of non-zero rows.

Rank= 3.

Question-6: Reduce the matrix ‘A’ to Normal form.

                                   A =

Sol. We have,

                                A =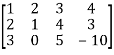

Apply

                                 A =

Apply ,       ,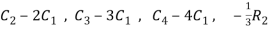  

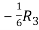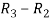
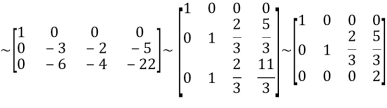
Apply

Which is the form of,

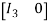                                            -  this is the normal form of A.

Question-7: Find the solution of the following homogeneous system of linear equations,

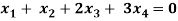
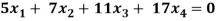
Sol. The given system of linear equations can be written in the form of matrix as follows,

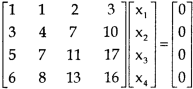
Apply the elementary row transformation,

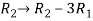
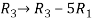
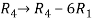  , we get,

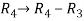    , we get

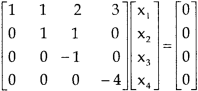
  Here r(A) = 4, so that it has trivial solution,

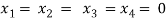
Question-8: check whether the following system of linear equations is consistent of not.

2x + 6y = -11

6x + 20y – 6z = -3

6y – 18z = -1

Sol. Write the above system of linear equations in augmented matrix form,

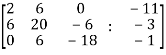
Apply 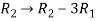 , we get

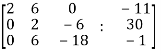
Apply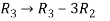

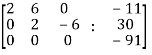
Here the rank of C is 3 and the rank of A is 2

Therefore both ranks are not equal. So that the given system of linear equations is not consistent.

Question-9: Check the consistency and find the values of x , y and z of the following system of linear equations.

2x + 3y + 4z = 11

X + 5y + 7z = 15

3x + 11y + 13z = 25

Sol. Re-write the system of equations in augmented matrix form.

                                  C = [A,B]

That will be,

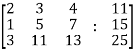
Apply 

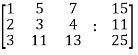
Now apply ,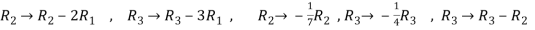 

We get,

  ~  ~

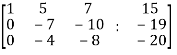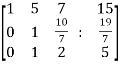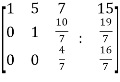
Here rank of A = 3

And rank of C = 3, so that the system of equations is consistent,

So that we can can solve the equations as below,

That gives,

x + 5y + 7z = 15  ……………..(1)

   y + 10z/7 = 19/7 ………………(2)

      4z/7 = 16/7 ………………….(3)

From eq. (3)

z = 4,

From 2,

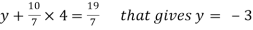
From eq.(1), we get

x + 5(-3) + 7(4) = 15

That gives,

                             x = 2

Therefore the values of x , y , z are    2 , -3 , 4  respectively.

Question-10: Solve the system of linear equations-

                       x + y + z = 3

                       x + 2y + 2z = 4

                       x + 4y + 9z = 6

9

Sol. These eq. Can be written in the form of matrix,

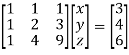
                         AX = B

Where,   A = 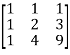   ,     X =     and   B =

Now we need to find out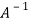   

We know that ,

                          =

Matrix of co-factors =

And

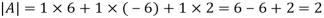
Then ,    will be,

We know that, 

                         X =

          X =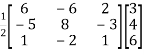

        X = =  =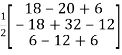

So that,

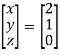
Here, x = 2 , y= 1 and z = 0.