Question Bank (unit-2)

Question-1: Find the characteristic equation of the matrix A:

                                A =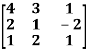

Sol. The characteristic equation will be-

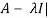                                               | = 0

                                  = 0

On solving the determinant, we get

(4-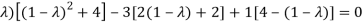

Or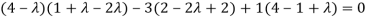

On solving we get,

Which is the characteristic equation of matrix A.

Question-2: Find the characteristic equation and characteristic roots of the matrix A:

                                A =

Sol. We know that the characteristic equation of the matrix A will be-

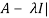                                  | = 0

So that matrix A becomes,

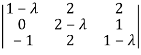                                    = 0

Which gives , on solving

              (1- = 0

Or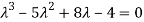                                

                 Or              (

Which is the characteristic equation of matrix A.

The characteristic roots will be,

                                  ( (

                                  (

                                   (

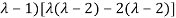
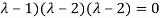
                 Values of 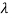are-

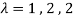
These are the characteristic roots of matrix A.

Question-3: Find out the Eigen values and Eigen vectors of ?

Sol.  The Characteristics equation is given by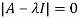

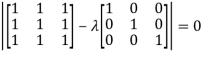
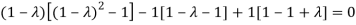
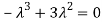
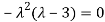
                                          Or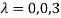

Hence the Eigen values are 0,0 and 3.

The Eigen vector corresponding to Eigen value 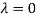is

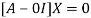
Where X is the column matrix of order 3 i.e.

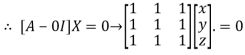
This implies that

Here number of unknowns are 3 and number of equation is 1.

Hence we have (3-1)=2 linearly independent solutions.

Let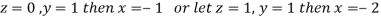

Thus the Eigen vectors corresponding to the Eigen value are (-1,1,0) and (-2,1,1).

The Eigen vector corresponding to Eigen value 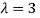is

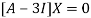
Where X is the column matrix of order 3 i.e.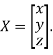

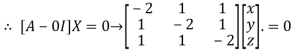
This implies that

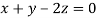
Taking last two equations we get

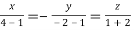
Or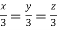

Thus the Eigen vectors corresponding to the Eigen value 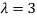are (3,3,3).

Hence the three Eigen vectors obtained are  (-1,1,0), (-2,1,1) and (3,3,3).

Question-4: Find out the Eigen values and Eigen vectors of

Sol.  Let A =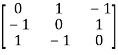

The characteristics equation of A is .

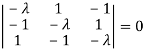
                                           Or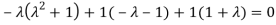 

                                                Or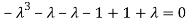 

                                                      Or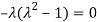

                                                       Or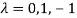

The Eigen vector corresponding to Eigen value 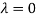is

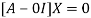
Where X is the column matrix of order 3 i.e.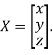

         Or

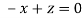
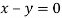
On solving we get 

Thus the Eigen vectors corresponding to the Eigen value is (1,1,1).

The Eigen vector corresponding to Eigen value 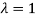is

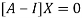
Where X is the column matrix of order 3 i.e.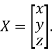

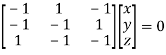
Or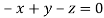    

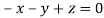
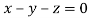
On solving 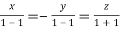or .

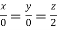Thus the Eigen vectors corresponding to the Eigen value is (0,0,2).

The Eigen vector corresponding to Eigen value 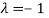is

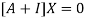
Where X is the column matrix of order 3 i.e.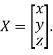

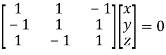
   Or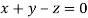    

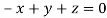
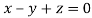
On solving we get 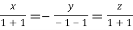   or .

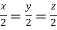Thus the Eigen vectors corresponding to the Eigen value 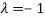is (2,2,2).

Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).

Question-5: Verify the Cayley-Hamilton theorem and find the inverse.

                  ?

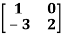Sol.  Let A =

The characteristics equation of A is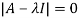

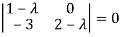
                                 Or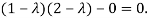

                                Or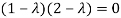 

                                 Or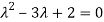 

By Cayley-Hamilton theorem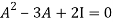 

                                   L.H.S:

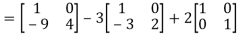
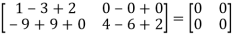                                                 =   =0=R.H.S

Multiply both side by 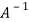on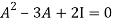 

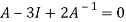
                                               Or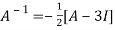

                                              Or [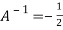

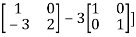
                                               Or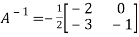

Question-6: Verify the Cayley-Hamilton theorem and find the inverse.

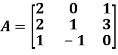
Sol. The characteristics equation of A is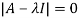

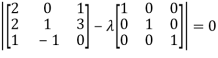
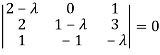
                                            Or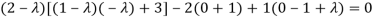

                                           Or

                                           Or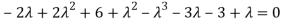

                                           Or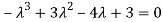

                                            Or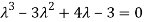

             By Cayley-Hamilton theorem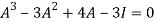

                L.H.S.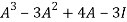

          =

=

=

Multiply both side with in

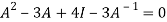
                                              Or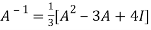

        Or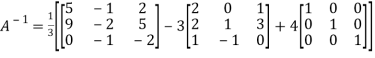

                     =

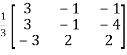
Question-7: Verify Cayley-Hamilton theorem for matrix A:

                                    A =

Sol.  Characteristic equation of matrix A will be,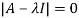  

                                     = 0

(2-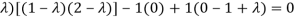

According to Cayley-Hamilton theorem,

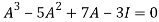                                           …………..(1)

Here we need to verify eq.(1)-

First we will find A² -

                            A² =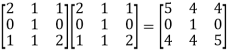

Now,

                          A³ = A².A =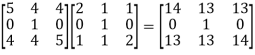

Equation (1) becomes,

                                    =

                                   =

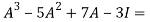
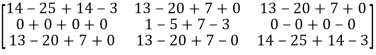
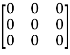
Hence the Cayley-Hamilton theorem is verified.

Question-8: Examine the following vectors to check whether they linearly dependent or independent and find the relationship if it exists.

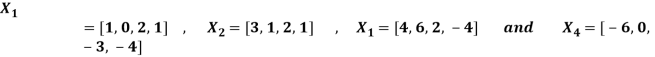
Sol. Let us consider the following matrix equation-

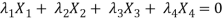                  ………………..(1)

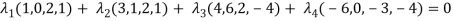
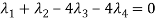
Matrix form of the above equations-

                                      =

Apply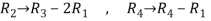

                                   =

Apply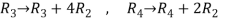 

                                 =

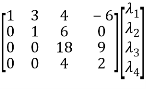Apply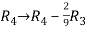 

                                =

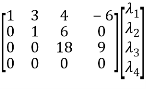Now, 

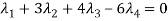
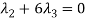
Suppose 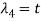    then

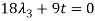
And,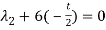  

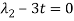
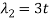
And,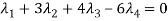  

Put these values in equation(1), we get

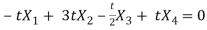
t is common here, so that

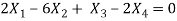
Question-9: suppose you have a matrix A = , then find the linear transformation of A.

Sol.     Here we have,

                                        A =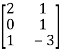

Multiply matrix A by vector (x,y).

                                              X = (x,y)

                          Ax =

We get, f(x,y) = (2x + y , y , x – 3y)

Which is the linear transformation of matrix A.

Question-10: find the linear transformation of the matrix A.

                                     A =

Sol. We have,

                                   A =

Multiply the matrix by vector x = (x , y , z) , we get

                                   Ax =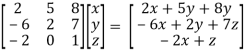

                                        = ( )

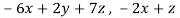f(x , y , z) = ( )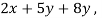

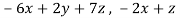Which is the linear transformation of A.

Question-11: Check whether the matrix A is orthogonal or not?

                              A =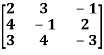

Sol. To check the orthogonality of this matrix , first we need to find AA’

So that,

        AA’ =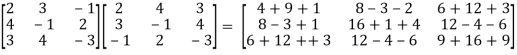

               =

Here AA’ ≠ I

So , we can say that matrix A is not an orthogonal matrix.

Question-12: If the matrix A defines an orthogonal transformation , then show that

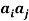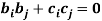+    ( i≠j)  i,j = 1 , 2 , 3.

Where            A =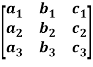

Sol.  As we know that an orthogonal matrix A ,

               AA’ = I = A’A     and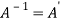 

We will find AA’,

        AA’ =   =

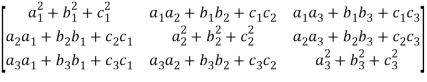
A will be orthogonal only if -    AA’ = I

In that case, it is only possible when,

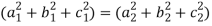= = 1

And,

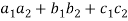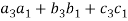() = () = () = 0