Question Bank (unit-3)

Question-: If x = cos

Sol. Here we are given,

                                        x =  cos, then

                       1 + 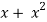= 1 + (cos

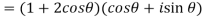
                                                                                                         Hence proved.

Question-2: If x = cos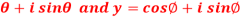 , then prove that,

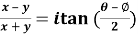
Sol. We are given,

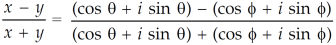
    On solving we get,

Question-3: Find out the modulus and principal argument of the following complex number-

                                                       .

Sol. Here we have,

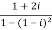
Now,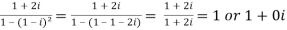   

Then, |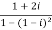| = |1 + 0i| =

Now, we know that the principal argument is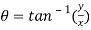 

Principal argument of 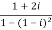   =  principal arg of 1 + 0i

                                                 =

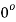
Therefore, modulus = 1 and argument =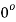

Question-4: If 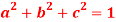and b + ic = (1 + a)z , then prove that

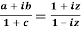
Sol. It is given that,

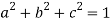                  and b + ic = (1 + a)z

We can write the second condition as-

Using right hand side,           

                                              =

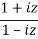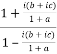
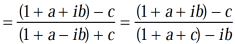
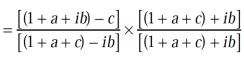
It becomes,

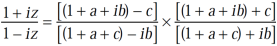
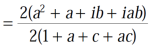
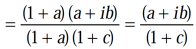
Question-5: If arg(z+1) = π/6 and arg (z – 1) = 2π/3  , then find the complex number.

Sol. Let us suppose, the complex numver is

                           z = x + iy   ……………..(1)

  Then,

                      z+1 = (x+1) + iy

The argument is also given,

Arg(z+1) = 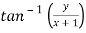=   π/6                                                    

                                                    ……………(1)

Now,

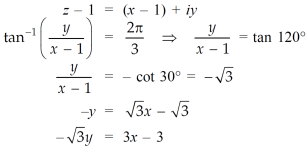
Adding this result with equation (1), we get,

                                                  0 = 4x – 2

                                                  4x = 2

                                                    X = ½

Put the value in (1), we get

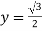
Therefore we got the values of x and y-

Put these values in (1) , we will get the complex number-

                       z =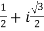

Which is the required complex number.

Question-6: Prove that

1.

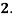
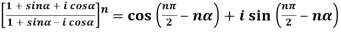
Sol. 1.

Similarly, we get

So that

Using the above results, we will solve the second condition-

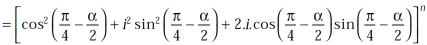
Use 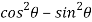= 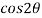and 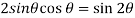, we get

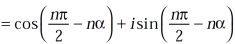                                                                               hence proved

Question-7: Solve 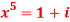 , also find the continued product of the roots.

Sol.  Here we have,

                                        =

Then,

                                    =

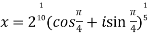
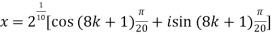
We will obtain the roots by putting k = 0 , 1 , 2 ,3,4….

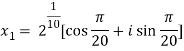
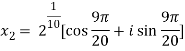
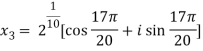
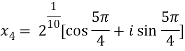
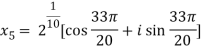
Now find the product of all these,

..

                                 =

                                 =

                                 = .

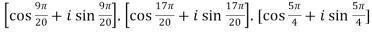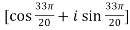
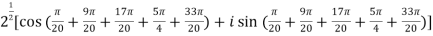
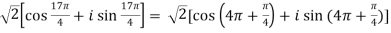
Question-8: prove that

Sol.  Here first we will take LHS-

              ……….(1)

Now , RHS

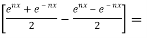
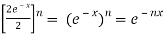
Therefore,

                                                        LHS = RHS

Question-9: If 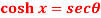, then prove that

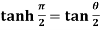
Sol. We have,   

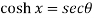
Put the value of cosh x, we get

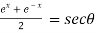
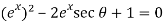
Solving the quadratic equation –

We get the value of

Now for the value of -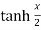

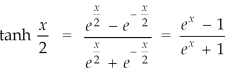
Using the above values, we get

                                                                                                                         Hence proved

Question-10: If 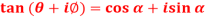, then prove that-

Sol. Here we are given,

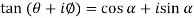
So that,

But,

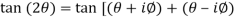
Using trigonometric formulae,

                                                                  =

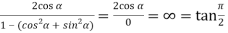
So that,

                  2

For general values,

                                          2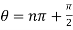  which is

Question-11: Prove that 

Sol.  Suppose   then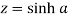  

And,

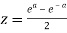
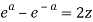
Or,

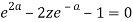
On solving the quadratic equation, we get-

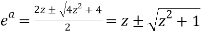
Then,

                                             ]                 

Or,

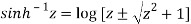
                                                             Hence proved.

Question-12: Prove that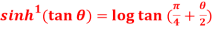

Sol. Using the formula-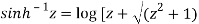 

We get,

                                                =

                                         =]

                                         = ]

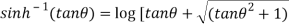
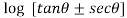
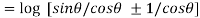
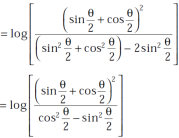
Take cos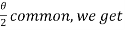

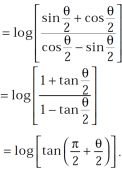
                                                                                                 Hence proved.

Question-13: If   , then prove that-

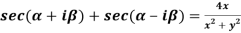
Sol. We take left hand side-

                                                                        =

                                                                        =

                                                                         =

                                                                         =

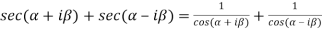
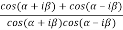
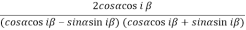
                                                                         =                           hence proved

Question-14: If , then prove that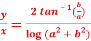

Sol. Here we have,

Taking log on both sides,

Implying,

Equating real and imaginary parts-

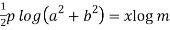                                     ………………. (1)

And,

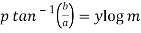                                     ……………………(2)                                        

Divide equation(2) by (1), we get

                                                                                                  Hence proved.