UNIT 3

Projections Of Straight Lines And Planes And Their Traces

1. Explain projection of lines parallel to one or both planes.

Ans -

Line Parallel to one or both the planes:

(a) Line AB is parallel to the H.P.

a and b are the top views of the ends A and B respectively. It can be clearly seen that the figure ABba is a rectangle. Hence, the top view ab is equal to AB. a'b' is the front view of AB and is parallel to xy.

(b) Line CD is parallel to the V.P.

The line c'd' is the front view and is equal to CD; the top view cd is parallel to xy.

(c) Line ff is parallel to the H.P. And the V.P.

Ef is the top view and e'f' is the front view; both are equal to ff and parallel to xy.

Hence, when a line is parallel to a plane, its projection on that plane is equal to its true length, while its projection on the other plane is parallel to the reference line.

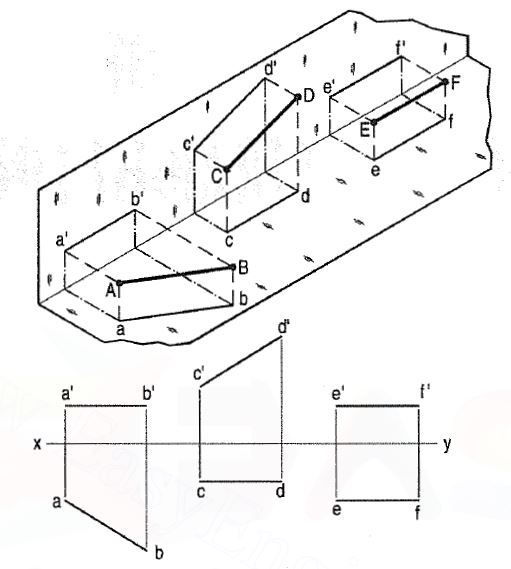
Figure 1

2. Explain projection of lines perpendicular to one or both planes.

Ans –

When a line is perpendicular to one reference plane, it will be parallel to the other.

Figure 2

(a) Line AB is perpendicular to the H.P. The top views of its ends coincide in the point a. Hence, the top view of the line AB is the point a. Its front view a' b' is equal to AB and perpendicular to xy.

(b) Line CO is perpendicular to the V.P. The point d' is its front view and the line cd is the top view. Cd is equal to CO and perpendicular to xy.

Hence, when a line is perpendicular to a plane its projection on that plane is

a point, while its projection on the other plane is a line equal to its true length and

Perpendicular to the reference line.

In first-angle projection method, when top views of two or more points coincide,

The point which is comparatively farther away from xy in the front view will be

Visible; and when their front views coincide, that which is farther away from xy in

The top view will be visible.

In third-angle projection method, it is just the reverse. When top views of two

Or more points coincide the point which is comparatively nearer xy in the front

View will be visible; and when their front views coincide, the point which is nearer xy in the top view will be visible.

3. Explain projection of lines inclined to other or both planes.

Ans –

The inclination of a line to a plane is the angle which the line makes with its

Projection on that plane.

(a) Line PQ1 [fig. 3(i)] is inclined at an angle 8 to the H.P. And is parallel

To the V.P. The inclination is shown by the angle 8 which PQ1 makes with

Its own projection on the H.P., viz. The top view pq1•

The projections [fig. 3(ii)] may be drawn by first assuming the line to

Be parallel to both the H.P. And the V.P. Its front view p’q’ and the top

View pq will both be parallel to xy and equal to the true length. When the

Line is turned about the end P to the position PQ1 so that it makes the

Angle 8 with the H.P. While remaining parallel to the V.P., in the front view

The point q’ will move along an arc drawn with p’ as centre and p’q’ as

Radius to a point q’1 so that p’q’ 1 makes the angle 8 with xy. In the top

View, q will move towards p along pq to a point q1 on the projector

Through q’1• p’q’1 and pq1 are the front view and the top view respectively

Of the line PQ1.

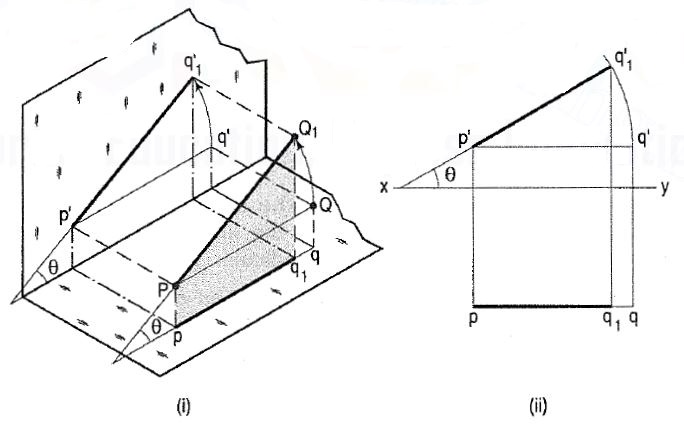
Figure 3

4. Explain line inclined to both the planes.

Ans –

(a) A line AB (fig. 4) is inclined at θ to the H.P. And is parallel to the V.P. The end A is in the H.P. AB is shown as the hypotenuse of a right-angled triangle, making the angle θ with the base.

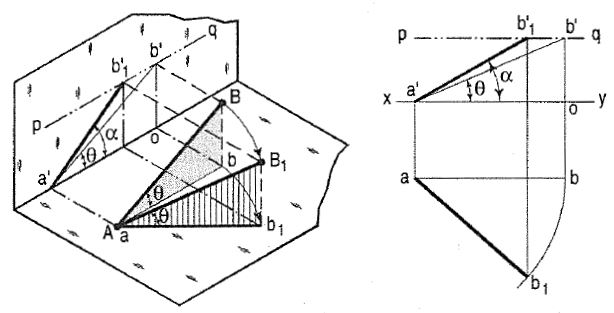
Figure 4

The top view ab is shorter than AB and parallel to xy. The front view a'b' is equal to AB and makes the angle θ with xy.

Keeping the end, A fixed and the angle θ with the H.P. Constant, if the end B is moved to any position, say B1, the line becomes inclined to the V.P. Also.

In the top view, b will move along an arc, drawn with a as centre and ab as radius, to a position b1. The new top view ab1 is equal to ab but shorter than AB.

In the front view, b' will move to a point b'1 keeping its distance from xy constant and equal to b'o; i.e. it will move along the line pq, drawn through b' and parallel to xy. This line pq is the locus or path of the end 8 in the front view. b'1 will lie on the projector through b1• The new front view a'b'1 is shorter than a'b' (i.e. AB) and makes an angle a with xy. A is greater than θ.

Thus, if the inclination θ of AB with the H.P. Is constant, even when it is inclined to the V.P.

(i) its length in the top view, viz. Ab remains constant; and

(ii) the distance between the paths of its ends in the front view, viz. b'o remains constant.

(b) The same line AB (fig. 5) is inclined at θ to the V.P. And is parallel to the H.P. Its end A is in the V.P. AB is shown as the hypotenuse of a right-angled triangle making the angle θ with the base.

5. Explain traces of lines.

Ans –

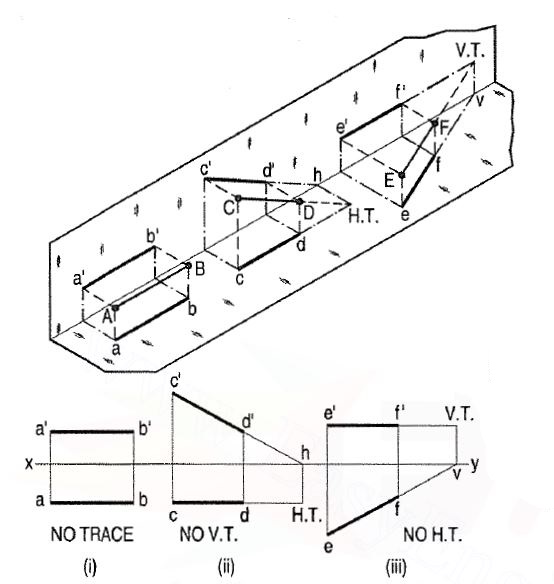
When a line is inclined to a plane, it will meet that plane, produced if necessary.

The point in which the line or line-produced meets the plane is called its trace.

The point of intersection of the line with the H.P. Is called the horizontal trace,

Usually denoted as H.T. And that with the V.P. Is called the vertical trace or V.T.

6. Explain projection of planes inclined to one or both planes?

Ans –

Perpendicular to one plane and inclined to the other plane:

(a) Plane, perpendicular to the H.P. And inclined to the V.P. (fig. 10).

A square ABCD is perpendicular to the H.P. And inclined at an angle φ to

The V.P. Its V.T. Is perpendicular to xy. Its H.T. Is inclined at φ to xy.

Its top view ab is a line inclined at φ to xy. The front view a'b'c'd' is

Smaller than ABCD.

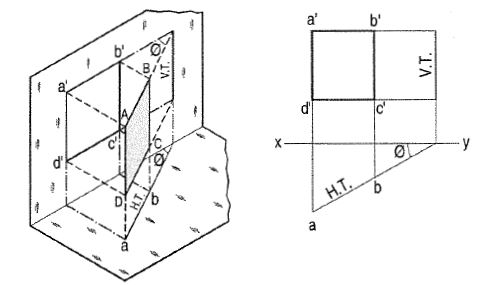
Figure 10

(b) Plane, perpendicular to the V.P. And inclined to the H.P. (fig. 11).

A square ABCD is perpendicular to the V.P. And inclined at an angle θ to

The H.P. Its H.T. Is perpendicular to xy. Its V.T. Makes the angle e with

Xy. Its front view a'b' is a line inclined at θ to xy. The top view abed is

a rectangle which is smaller than the square ABCD.