UNIT 4

Projections Of Solids

1. Explain different types of solids?

Ans –

(1) Polyhedra

(2) Solids of revolution.

Polyhedra: A polyhedron is defined as a solid bounded by planes called faces. When all faces are equal and regular, the polyhedron is said to be regular. There are seven regular polyhedra which may be defined as stated below:

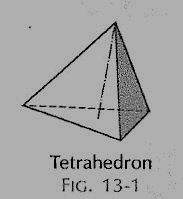
(i) Tetrahedron (fig.): It has four equal faces, each an equilateral triangle.

Figure

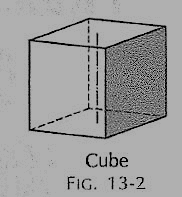
(ii) Cube or hexahedron (fig.): It has six faces, all equal squares.

Figure

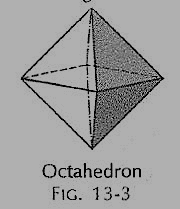
(iii) Octahedron (fig.): It has eight equal equilateral triangles as faces.

Figure

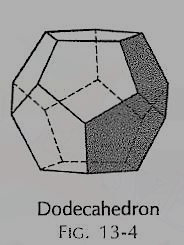
(iv) Dodecahedron (fig.): It has twelve equal and regular pentagons as faces.

Figure

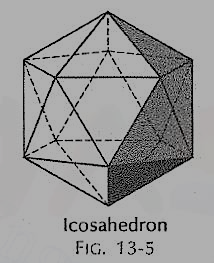
(v) Icosahedron (fig.): It has twenty faces, all equal equilateral triangles.

Figure

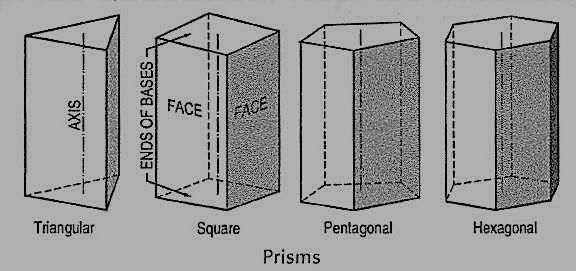
(vi) Prism: This is a polyhedron having two equal and similar faces called its ends or bases, parallel to each other and joined by other faces which are parallelograms. The imaginary line joining the centres of the bases is called the axis. A right and regular prism (fig.) has its axis perpendicular to the bases. All its faces are equal rectangles.

Figure

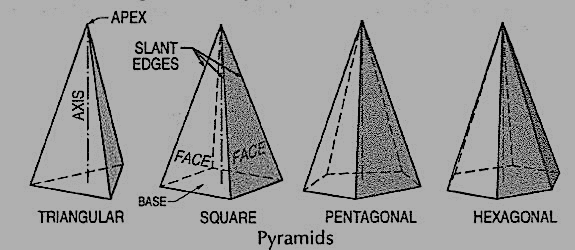
(vii) Pyramid: This is a polyhedron having a plane figure as a base and many triangular faces meeting at a point called the vertex or apex. The imaginary line joining the apex with the centre of the base is its axis.

A right and regular pyramid (fig.) has its axis perpendicular to the base which is a regular plane figure. Its faces are all equal isosceles triangles.

Figure

Oblique prisms and pyramids have their axes inclined to their bases. Prisms and pyramids are named according to the shape of their bases, as triangular, square, pentagonal, hexagonal etc.

2. Explain projections of solids with axis perpendicular and parallel to HP and VP.

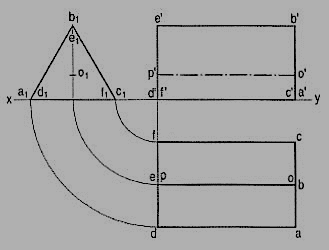
A triangular prism1 base 40 mm side and height 65 mm is resting on the H.P. On one of its rectangular faces with the axis parallel to the V.P. Draw its projections.

As the axis is parallel to both the planes, begin with the side view.

(i) Draw an equilateral triangle representing the side view, with one side in xy.

(ii) Project the front view horizontally from this triangle.

(iii) Project down the top view from the front view and the side view, as shown.

Figure

3. Projections of solids with axis inclined to one of the reference planes and parallel to the other.

Ans –

When a solid has its axis inclined to one plane and parallel to the other, its projections are drawn in two stages.

(1) In the initial stage, the solid is assumed to be in simple position, i.e. its axis perpendicular to one of the planes.

If the axis is to be inclined to the ground, i.e. the H.P., it is assumed to be perpendicular to the H.P. In the initial stage. Similarly, if the axis is to be inclined to the V.P., it is kept perpendicular to the V.P. In the initial stage.

Moreover

(i) if the solid has an edge of its base parallel to the H.P. Or in the H.P. Or on the ground, that edge should be kept perpendicular to the V.P.; if the edge of the base is parallel to the V.P. Or in the V.P., it should be kept perpendicular to the H.P.

(ii) If the solid has a corner of its base in the H.P. Or on the ground, the sides of the base containing that corner should be kept equally inclined to the V.P.; if the corner is in the V.P., they should be kept equally inclined to the H.P.

4. Solids with axis inclined to one or both the planes.

Ans –

When a solid has its axis inclined to one plane and parallel to the other, its

Projections are drawn in two stages.

(1) In the initial stage, the solid is assumed to be in simple position, i.e. its

Axis perpendicular to one of the planes.

If the axis is to be inclined to the ground, i.e. the H.P., it is assumed

To be perpendicular to the H.P. In the initial stage. Similarly, if the axis is to

Be inclined to the V.P., it is kept perpendicular to the V.P. In the initial stage.

Moreover

(i) if the solid has an edge of its base parallel to the H.P. Or in the H.P.

Or on the ground, that edge should be kept perpendicular to the V.P.;

If the edge of the base is parallel to the V.P. Or in the V.P., it should

Be kept perpendicular to the H.P.

(ii) If the solid has a corner of its base in the H.P. Or on the ground,

The sides of the base containing that corner should be kept equally

Inclined to the V.P.; if the corner is in the V.P., they should be kept

Equally inclined to the H.P.

5. Projections of spheres touching each other.

Ans –

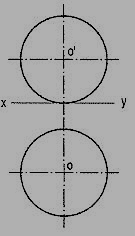
The projection of a sphere in any position on any plane is always a circle whose diameter is equal to the diameter of the sphere (fig. 13-48). This circle represents the contour of the sphere.

Figure

A flat circular surface is formed when a sphere is cut by a plane. A hemisphere (i.e. a sphere cut by a plane passing through its centre) has a flat circular face of diameter equal to that of the sphere.

When it is placed on the ground on its flat face, its front view is a semi-circle, while its top view is a circle [fig.].

When the flat face is inclined to the H.P. Or the ground and is perpendicular to the V.P. It is an ellipse (partly hidden) in the top view [fig], while the contour of the hemisphere is shown by the arc of the circle drawn with radius equal to that of the sphere.

Fig shows the projections of a sphere, a small portion of which is cut off by a plane. Its flat face is perpendicular to the H.P. And inclined to the V.P. An ellipse is seen in the front view within the circle for the sphere.

Figure        Figure

6. How are spheres in contact with each other defined?

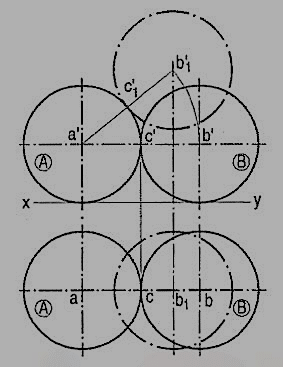
Projections of two equal spheres resting on the ground and in contact with each other, with the line joining their centres parallel to the V.P., are shown in fig. 25.

Figure

As the spheres are equal in size, the line joining their centres is parallel to the ground also. Hence, both ab and a'b' show the true length of that line (i.e. equal to the sum of the two radii or the diameter of the spheres). The point of contact between the two spheres is also visible in each view.

If the position of one of the spheres, say sphere B, is changed so that the line joining their centres is inclined to the V.P., in the front view, the centre b' will move along the line a'b' to b'1. The true length of the line joining the centres and the point of contact are now seen in the top view only.

When the sphere B is so moved that it remains in contact with the sphere A and the line joining their centres is parallel to the V.P., but inclined to the ground (fig.),the true length of that line and the point of contact are visible in the front view only.

Figure

7. A brass flower-vase is spherical in shape with flat, circular top 35 cm diameter and bottom 25 cm diameter and parallel to each other. The greatest diameter is 40 cm. Draw the projections of the vase when its axis is parallel to the V.P. And makes an angle of 60° with the ground. (fig)

(i) Draw the front view of the vase resting on its bottom with its axis vertical. Project the top view.

(ii) Tilt the front view so that the axis makes 60° angle with xy and project the top view. Note that a part of the ellipse for the bottom is also visible.

Figure